Динамика эпс. Вариант 68. Исходные данные 4 расчет динамического паспорта тележки при движении
 Скачать 1.13 Mb. Скачать 1.13 Mb.
|
1.3 Расчет второй критической скорости в кривойВторая критическая скорость соответствует границе между свободным положением и положением наибольшего перекоса тележки при ее движении в круговой части кривой. Выбор расчетной схемы осуществляется в зависимости от соотношения между заданной величиной жесткой базы тележки 2ат и рассчитанным в п. 1.1 курсовой работы граничным значением полюсного расстояния хmax. Т.к. выполняется условие хmax > ат. то приводим расчетную схему, показанную на рисунке 1.4, в соответствии с которой производим дальнейший расчет. Вторая критическая скорость в этом случае определяется по следующей формуле: 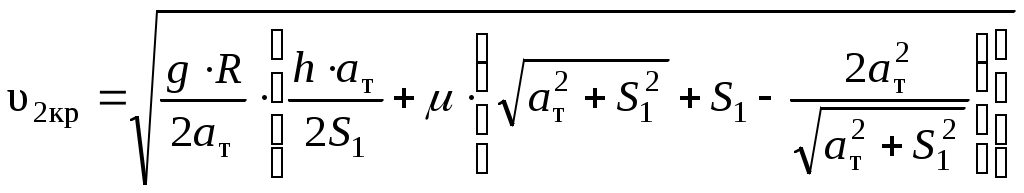 . (1.9) . (1.9)Расчеты по формуле (1.9) выполняем для кривой без возвышения и с возвышением наружного рельса. В рассматриваемом случае реакция внутренней грани головки наружного рельса на давление гребня колеса передней колесной пары рассчитывается по формуле: 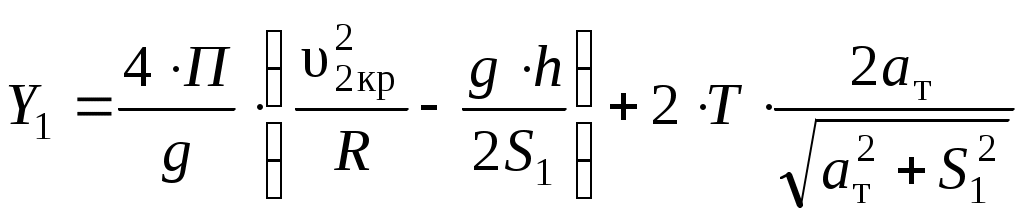 (1.10) (1.10)Рисунок 1.4 – Расчетная схема тележки для определения υ2кр Расчеты по формуле (1.10) также выполняем для кривой без возвышения и с возвышением наружного рельса. Силу бокового давления Yб1 определяем по формуле (1.6), сила бокового давления Yб2 = 0. Согласно применяемой для расчета схеме соs2 = 0, так как угол 2 = 90°, следовательно, задняя колесная пара тележки в этом случае не оказывает бокового давления на рельсы в кривой. Значение cos1 для определения силы Yб1 рассчитываем по формуле: Значение силы Yб1 по формуле (1.6) рассчитываем для кривой без возвышения и с возвышением наружного рельса. Примеры расчетов: Рассчитываем вторую критическую скорость движения в кривой без возвышения наружного рельса (h = 0): 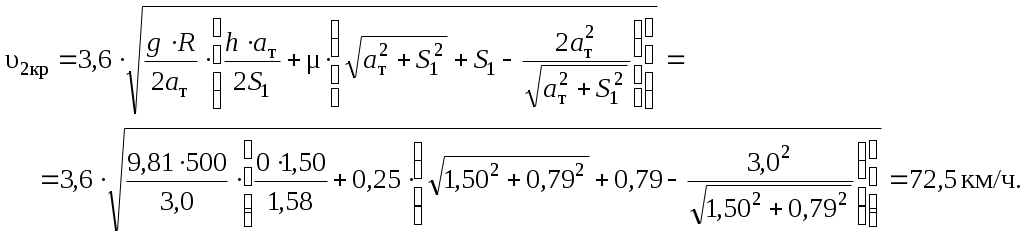 Находим направляющую силу: 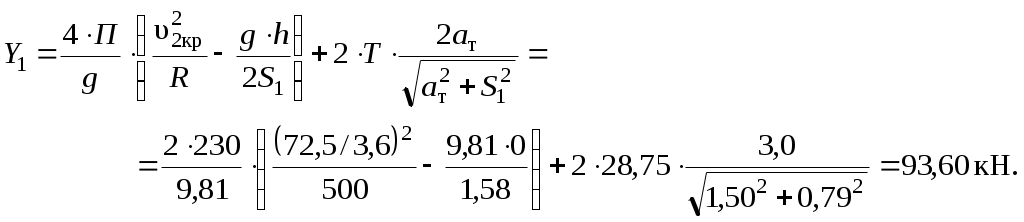 Определим величину бокового давления первой колесной пары на рельс: Аналогично выполним расчет для кривой с возвышением наружного рельса: 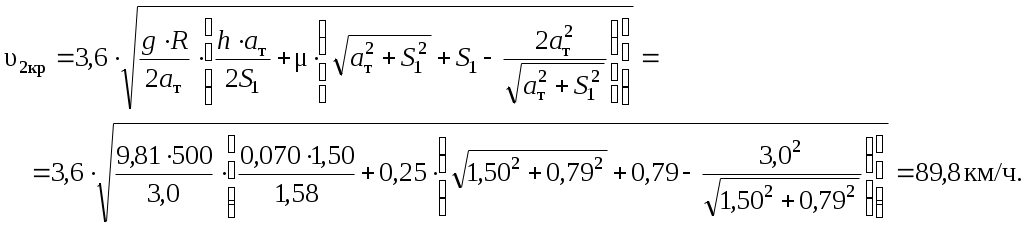 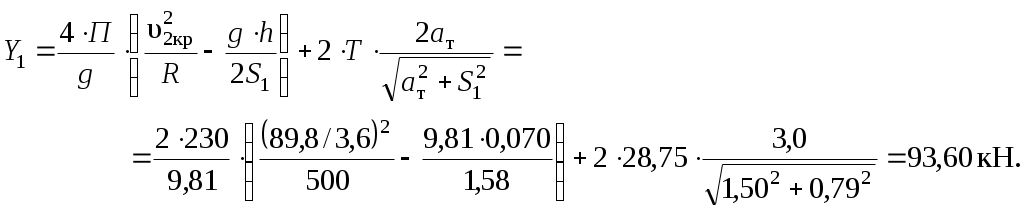 1.4 Расчет положения наибольшего перекоса тележки в кривой Диапазон скоростей, при которых тележка в круговой кривой устанавливается в положение наибольшего перекоса, 0 < υ < υ2кр. Выбор расчетной схемы зависит в первую очередь от соотношения между xmax и 2ат. Т.к. xmax > 2ат, то применяем расчетную схему, показанную на рисунке 1.5. Т.к. выполняется условие xmax > 2ат, то на первом этапе расчета необходимо определить скорость, при которой отсутствует набегание гребня колеса задней колесной пары тележки на рабочую грань головки внутреннего рельса кривой: где 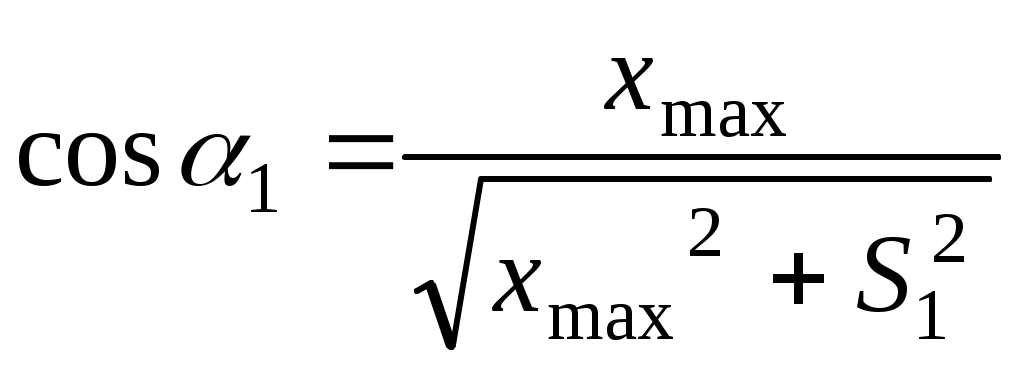 (1.13) (1.13)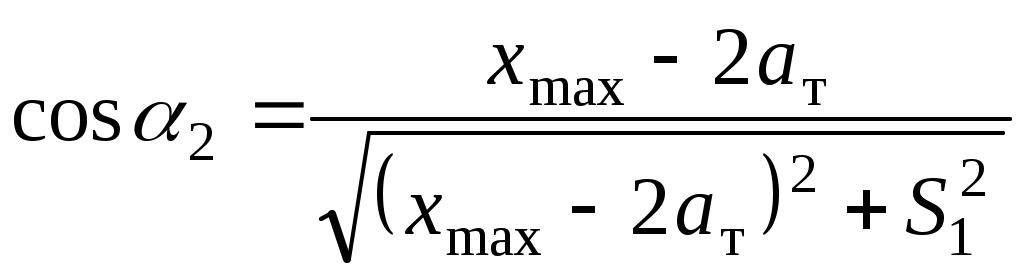 (1.14) (1.14)Рисунок 1.5 – Расчетная схема тележки для расчета положения наибольшего перекоса при набегании колеса второй колесной пары на внутренний рельс Расчеты по формуле (1.12) выполняем для кривой без возвышения и с возвышением наружного рельса. Если подкоренное выражение в формуле (1.12) отрицательно или равно нулю, то набегание гребня колеса задней колесной пары тележки на рабочую грань головки внутреннего рельса кривой отсутствует, и в качестве расчетной схемы для всего диапазона скоростей положения наибольшего перекоса используем схему, показанную на рисунке 1.6. Так как набегание отсутствует, то значения силы Y2 в положении наибольшего перекоса для любого значения расчетной скорости равны нулю (колонка 3 таблиц 1.1 и 1.2). Рисунок 1.6 – Расчетная схема тележки для расчета положения наибольшего перекоса при отсутствии набегания колеса второй колесной пары на внутренний рельс При отсутствии набегания величина полюсного расстояния величина x переменна, и на следующем этапе расчета необходимо построить графическую зависимость величины центробежной силы тележки от величины x, то есть Ст = f(x). Для ее построения используется следующее выражение: 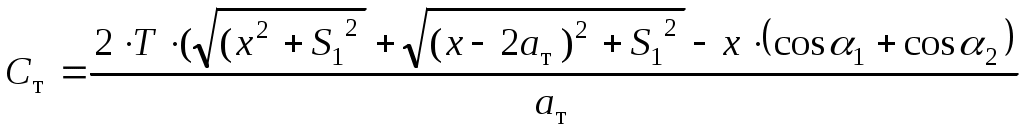 , (1.15) , (1.15)где 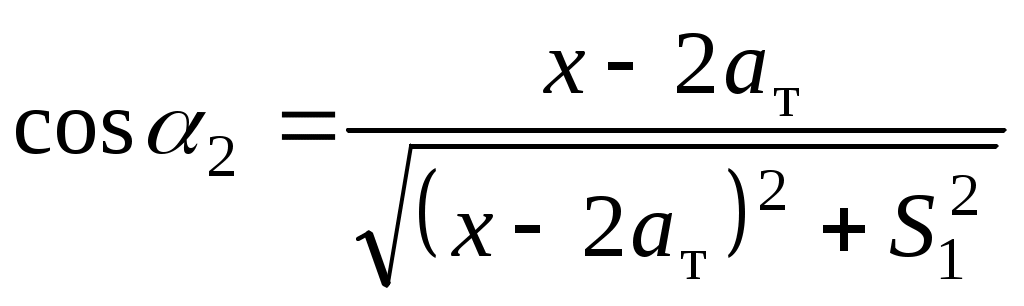 . (1.17) . (1.17)При построении зависимости Ст = f(x) крайними значениями x являются ат и xmax. График зависимости показан на рисунке 1.7. На следующем этапе для каждого значения скорости рассчитываем соответствующее значение центробежной силы тележки Ст по формуле: Для рассчитанного значения по графику зависимости Ст = f(x) определяем соответствующее значение x и заносим в шестую колонку таблиц 1.1 и 1.2. Расчеты по формуле (1.18) выполняем для кривой без возвышения и с возвышением наружного рельса. Величину реакции Y1 при отсутствии набегания гребня колеса задней колесной пары тележки на рабочую грань головки внутреннего рельса кривой определяем по формуле: В формуле (1.19) в качестве Ст используем значения, ранее определенные для соответствующих скоростей по формуле (1.18), а косинусы углов рассчитываем по формулам (1.16) и (1.17), при этом значения x для соответствующих расчетных скоростей выбираем из шестой колонки таблиц 1.1 или 1.2. Силы бокового давления Yб1 и Yб2 в этом случае рассчитываем по формулам (1.6) и (1.7). Расчеты по формулам (1.18), (1.6) и (1.7) выполняем для кривой без возвышения и с возвышением наружного рельса, результаты заносим в соответствующие колонки таблиц 1.1 и 1.2. Если подкоренное выражение в формуле (1.12) положительно, то при скоростях, меньших υо, наблюдается набегание гребня колеса задней колесной пары тележки на рабочую грань головки внутреннего рельса кривой, а при скоростях, равных или больших υо – отсутствие набегания. В строке, соответствующей скорости υо, значение Y2 равно 0, а полюсное расстояние x равно xmax. Для скоростей υ> υо, то есть при отсутствии набегания, применяем рассмотренную ранее расчетную схему (рисунок 1.6) и изложенную выше методику расчета, начиная с построения зависимости Ст = f(x). 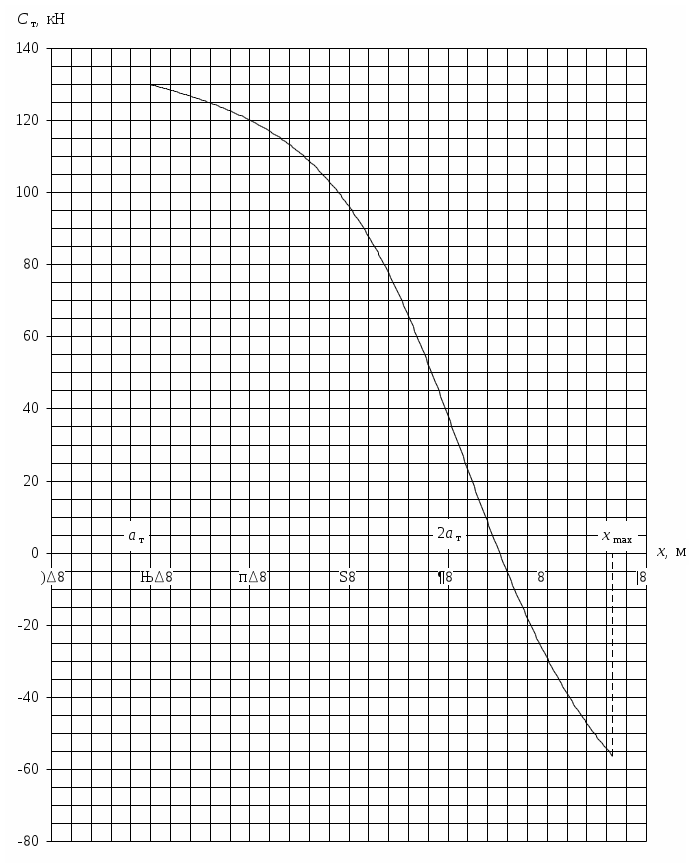 Рисунок 1.7 – График зависимости Ст = f(x) При скоростях υ < υо, то есть при наличии набегания, применяем расчетную схему, показанную на рисунке 1.5. В этом случае полюсное расстояние для всего указанного диапазона скоростей постоянно и равно xmax. На первом этапе расчета для каждой расчетной скорости необходимо вычислить значение центробежной силы тележки, используя для этого формулу (1.18). После этого для каждой скорости по формулам: определяем реакции рельсов, а по формулам (1.6) и – силы бокового давления. Расчеты по формулам (1.18), (1.20). (1.21), (1.6) и (1.22) выполняем для кривой без возвышения и с возвышением наружного рельса; для определения параметра А и косинусов углов используем формулы (1.12), (1.13) и (1.14). Результаты расчетов динамических сил в положении наибольшего перекоса для кривой без возвышения и с возвышением наружного рельса сводим в таблицы 1.1 и 1.2. Шаг расчета – 5 км/ч, интервал скорости – от 0 до υ2кр. Примеры расчетов: Находим величину параметра А: 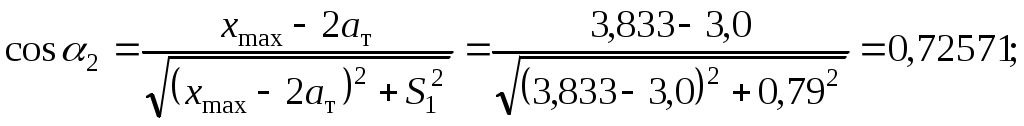 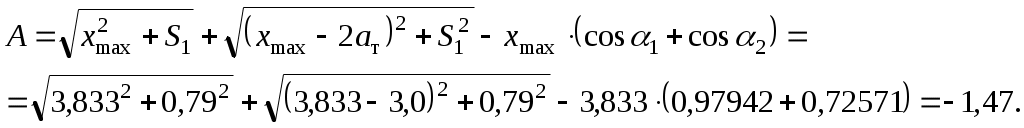 Определяем скорость, при которой будет набегание колеса второй колесной пары на внутренний рельс в кривой без возвышения наружного рельса (h = 0): Подкоренное выражение отрицательно, поэтому набегание второй колесной пары на внутреннюю рабочую грань рельса отсутствует. Рассмотрим пример расчетов для этой кривой при скорости υ = 10 км/ч. По формуле (1.18) определяем Ст при υ = 10 км/ч: 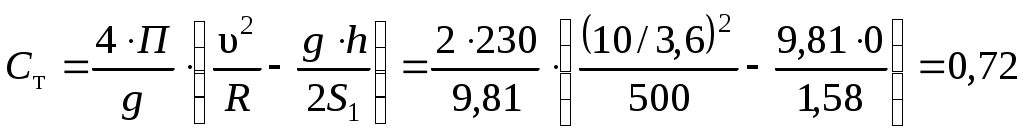 кН. кН.По графику зависимости Ст = f(x) (рисунок 1.7) определяем, что при Ст = 0,72 кН полюсное расстояние x = 3,254 м. 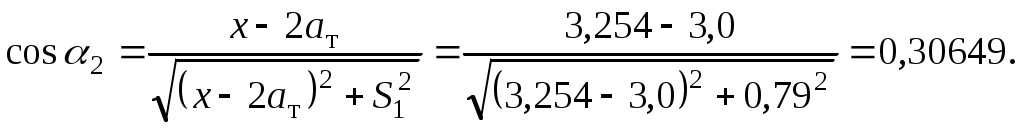 Сила реакции наружного рельса: Силы бокового давления рельсов: Аналогично выполним расчеты для кривой c возвышением наружного рельса. Находим скорость, при которой отсутствует набегание гребня колеса задней колесной пары на головку внутреннего рельса Подкоренное выражение отрицательно, поэтому набегание второй колесной пары на внутреннюю рабочую грань рельса отсутствует. Рассмотрим пример расчетов для этой кривой при скорости υ = 10 км/ч. По формуле (1.18) определяем Ст при υ = 10 км/ч: 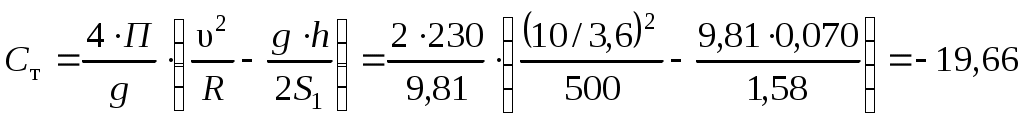 кН. кН.По графику зависимости Ст = f(x) (рисунок 1.7) определяем, что при Ст = -19,66 кН полюсное расстояние x = 3,413 м. 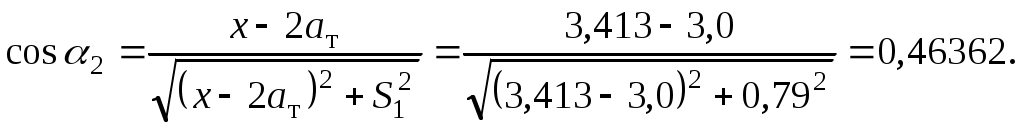 Сила реакции наружного рельса: Силы бокового давления рельсов: |
