Динамика эпс. Вариант 68. Исходные данные 4 расчет динамического паспорта тележки при движении
 Скачать 1.13 Mb. Скачать 1.13 Mb.
|
1.5 Расчет свободного положения тележки в кривойДиапазон скоростей, при которых тележка в круговой кривой устанавливается в свободное положение, υ2кр < υ < υ1кр. Для расчета используем расчетную схему, показанную на рисунке 1.8. Указанный диапазон скоростей разбиваем на интервалы, и соответствующие значения расчетных скоростей заносим в первую колонку таблиц 1.1 и 1.2. В третью колонку записываем нулевые значения, так как для любой скорости движения в свободном положении отсутствует набегание гребней задней колесной пары на головки рельсов, то есть реакция Y2 = 0. Рисунок 1.8 – Расчетная схема тележки для расчета свободного положения тележки в кривой Так как полюсное расстояние в свободном положении есть величина переменная, то на первом этапе расчета используем графическую зависимость величины центробежной силы, действующей на тележку, от полюсного расстояния Ст = f(x) (рисунок 1.7), построенную ранее. На следующем этапе расчета для каждого значения скорости определяем соответствующее значение центробежной силы тележки по формуле (1.18), а затем по графику зависимости. Ст = f(x) – соответствующее ему значение x, которое записываем в шестую колонку таблиц 1.1 и 1.2. Величину реакции наружного рельса определяем по формуле а силы бокового давления - по формулам (1.6) и (1.7). Значения косинусов углов, используемые для свободного положения в формулах (1.23), (1.6) и (1.7), определяем по формулам (1.16) и (1.17). В качестве Ст в формуле (1.23) используем значения, ранее рассчитанные для соответствующих скоростей по формуле (1.18), а значения x выбираем из шестой колонки таблицы 1.1 или 1.2 для свободного положения тележки. Расчеты свободного положения тележки производим для кривой без возвышения и с возвышением наружного рельса. Результаты расчетов сведены в таблицы 1.1 и 1.2. Шаг расчета 5 км/ч. Примеры расчетов: Производим расчет для кривой без возвышения наружного рельса. Рассмотрим пример расчетов при скорости υ = 80 км/ч. По формуле (1.18) определяем Ст при υ = 80 км/ч: 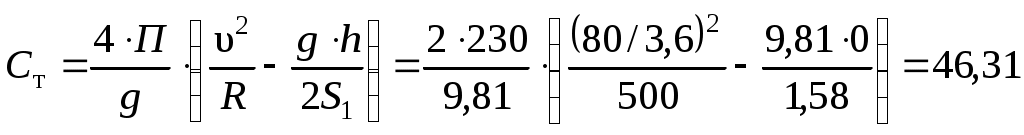 кН. кН.По графику зависимости Ст = f(x) (рисунок 1.7) определяем, что при Ст = 46,31 кН полюсное расстояние x = 2,943 м. 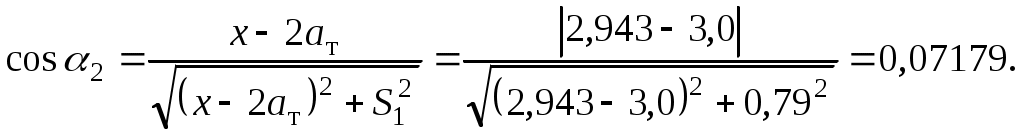 Сила реакции наружного рельса: Силы бокового давления рельсов: Аналогично выполним расчет свободного положения для кривой с возвышением. Рассмотрим пример расчетов при скорости υ = 100 км/ч. По формуле (1.18) определяем Ст при υ = 100 км/ч: 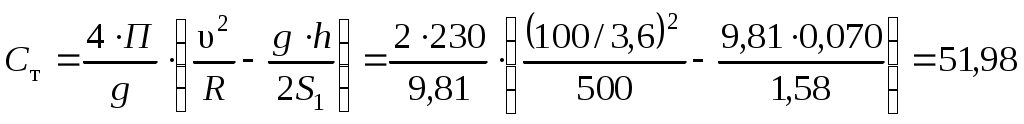 кН. кН.По графику зависимости Ст = f(x) (рисунок 1.7) определяем, что при Ст = 51,98 кН полюсное расстояние x = 2,903 м. 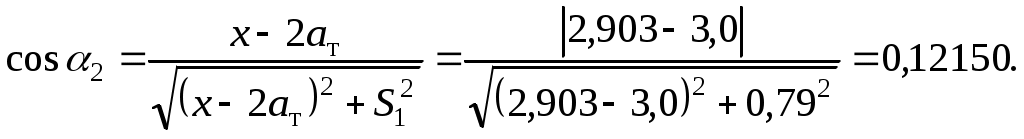 Сила реакции наружного рельса: Силы бокового давления рельсов: 1.6 Расчет хордового положения тележки в кривойСкорости, при которых тележка в круговой кривой устанавливается в хордовое положение, υ1кр < υ < υк. Расчетная схема тележки для расчета хордового положения показана на рисунке 1.9. На первом этапе расчета по формуле (18) для каждого значения скорости рассчитывается центробежная сила Ст, действующая на тележку. Затем для каждого значения скорости производится расчет реакций рельсов по следующим формулам: 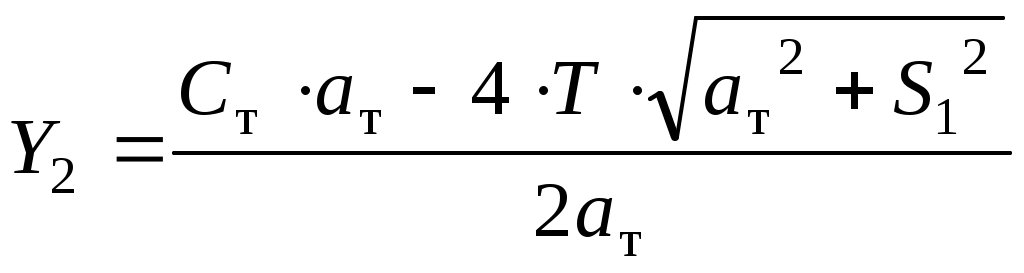 , (1.24) , (1.24)После определения реакций рельсов, по формулам (1.6) и (1.22) рассчитываются силы бокового давления, при этом косинусы углов одинаковы и определяются по формуле (1.8). Рисунок 1.9 – Расчетная схема тележки для расчета хордового положения тележки в кривой Т.к. конструкционная скорость заданного локомотива ниже, чем первые критические скорости для кривой без возвышения и с возвышением наружного рельса, то тележка не установится в хордовое положение. Поэтому расчеты хордового положения не производим. Результаты расчетов сведены в таблицы 1.1 и 1.2, которые представляют собой динамические паспорта заданной тележки при движении в кривой радиусом 500 м без возвышения наружного рельса и с возвышением 70 мм. Таблица 1.1 – Динамический паспорт тележки при движении в кривой R = 500 м, h = 0 мм
Таблица 1.2 – Динамический паспорт тележки при движении в кривой R = 500 м, h = 70 мм
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
