Динамика эпс. Вариант 68. Исходные данные 4 расчет динамического паспорта тележки при движении
 Скачать 1.13 Mb. Скачать 1.13 Mb.
|
1.1 Расчет граничных значений полюсного расстояния тележки в кривойПри движении в кривой заданного радиуса R с некоторой поступательной скоростью υ тележка совершает поворот относительно мгновенного центра вращения или полюса , расстояние до которого от оси первой по ходу движения колесной пары называется полюсным расстоянием x (рисунок 1.1). Полюсное расстояние есть величина переменная, зависящая от положения тележки в кривой, скорости движения и параметров кривой и тележки. Рисунок 1.1 – Параметры, определяющие расположение двухосной тележки в круговой кривой Граничные значения полюсного расстояния x, м определяем по формулам: где 2ат – заданная жесткая база тележки, м; R – заданный радиус кривой, м; ∆ – величина зазора в рельсовой колее, м. Величина зазора между гребнями колес и внутренними боковыми гранями головок рельсов (величина зазора в рельсовой колее) зависит от ширины рельсовой колеи в кривой 2Sкр, расстояния между внутренними гранями колес и толщины гребней. Схема для определения величины зазора показана на рисунке 1.2. Рисунок 1.2 – Схема для определения величины зазора в рельсовой колее В кривых радиусом более 350 м ширина колеи составляет 2Sкр = 1520 мм. Расстояние между боковыми гранями колес составляет 1440 мм, толщина неизношенного гребня 33 мм. Поэтому = 1520 – 1440 – 2·33 = 1520 – 1506 = 14 мм. Находим границы полюсного расстояния: 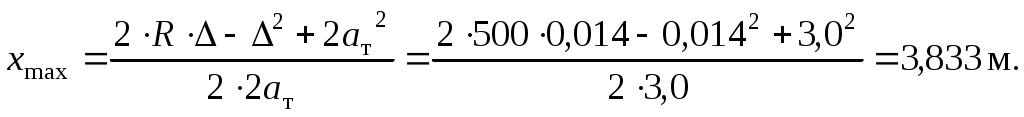 1.2 Расчет критических скоростей при движении в кривойСогласно [1], тележка электровоза при движении с постоянной скоростью в круговой кривой может занимать одно из следующих положений: наибольшего перекоса, когда экипаж направляется обеими рельсовыми нитями, наружной и внутренней; свободное, когда тележка направляется лишь одной внешней рельсовой нитью; реборды колес задней оси не касаются рельсов колеи; хордовое, когда передние и задние оси экипажа направляются наружной рельсовой нитью. С ростом скорости тележка устанавливается из положения наибольшего перекоса в свободное и далее в хордовое положение. Каждому из положений соответствует своя схема сил взаимодействия колес и рельсов. Скорость, при которой тележка переходит из одного положения в другое, принято называть критической. Первая критическая скорость соответствует границе между хордовым и свободным положением тележки, вторая критическая скорость – границе между свободным положением и положением наибольшего перекоса. Расчетная схема тележки для определения первой критической скорости приведена на рисунке 1.3. Рисунок 1.3 – Расчетная схема тележки для определения υ1кр Силы трения в точках контакта поверхностей катания колес с поверхностями катания головок рельсов определим по формуле: где – коэффициент трения колес о рельсы, принимаем = 0,25; П – вертикальная нагрузка от колеса на рельс, определяем по заданной нагрузке от колесной пары на рельсы 2П, кН. Первая критическая скорость, км/ч рассчитывается по следующей формуле: 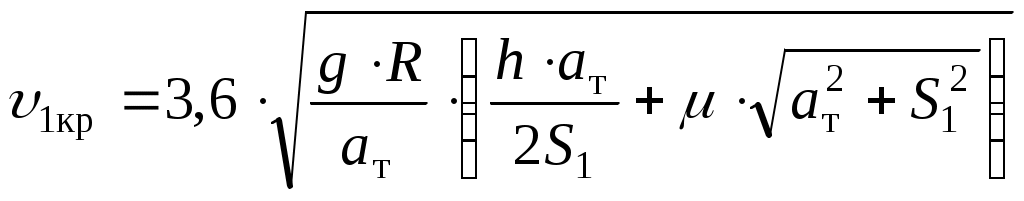 (1.4) (1.4)где g = 9,81 м/с2 – ускорение силы тяжести; h – возвышение наружного рельса, м; 2S1 = 1,58 м – расстояние между точками контакта поверхностей качания колес и головок рельсов, м. Расчеты по формуле (1.4) выполняем для заданной кривой без возвышения наружного рельса, т.е. при h = 0 и с заданным возвышением наружного рельса h. Реакцию внутренней грани головки наружного рельса на давление гребня колеса передней колесной пары (направляющую силу) рассчитаем по формуле: 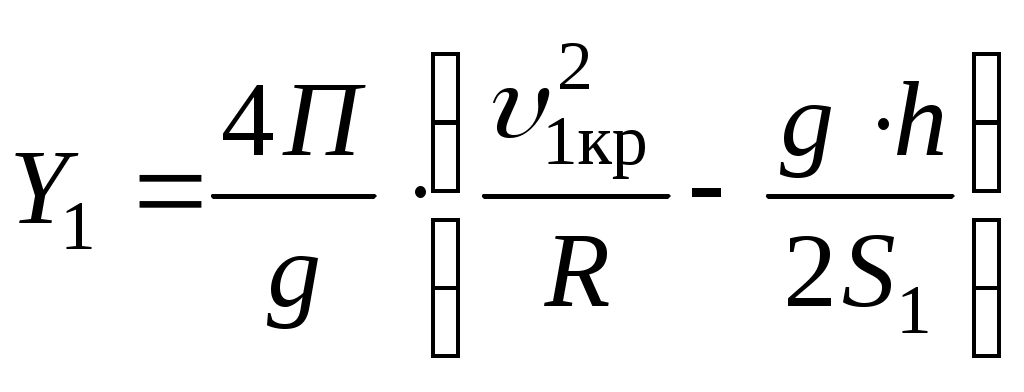 (1.5) (1.5)Расчеты по формуле (1.5) также выполняем для кривой без возвышения и с возвышением наружного рельса. На следующем этапе расчета определим силы бокового давления в точках контакта колес с наружным рельсом: где cos1, cos2 - косинусы углов наклона лучей относительно продольной оси тележки. В соответствии с применяемой в этом случае расчетной схемой значения cos1, cos2 одинаковы и определяются по формуле: Силы Yб1 и Yб2 также рассчитываем для кривой без возвышения и с возвышением наружного рельса. Примеры расчетов: Находим силу трения колес о рельсы: Определим первую критическую скорость в кривой без возвышения наружного рельса (h = 0): 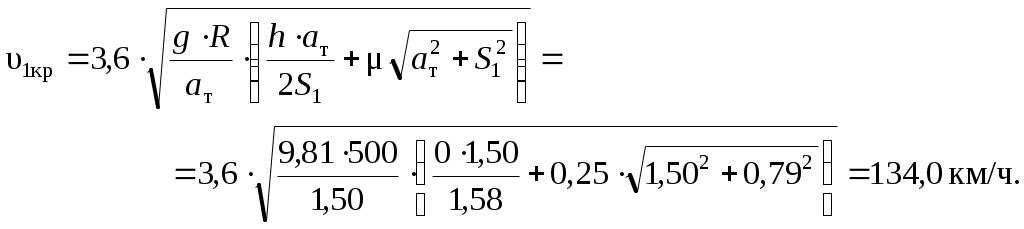 Найдем величину направляющей силы: 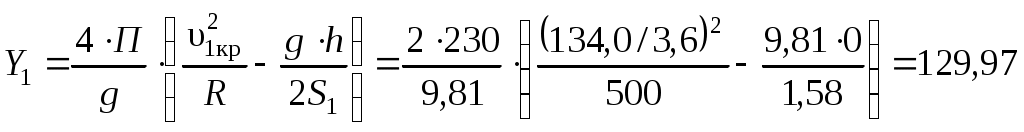 кН. кН.Найдем силу бокового давления колес на рельсы: Определим первую критическую скорость в кривой c возвышением наружного рельса (h = 0,070 м): 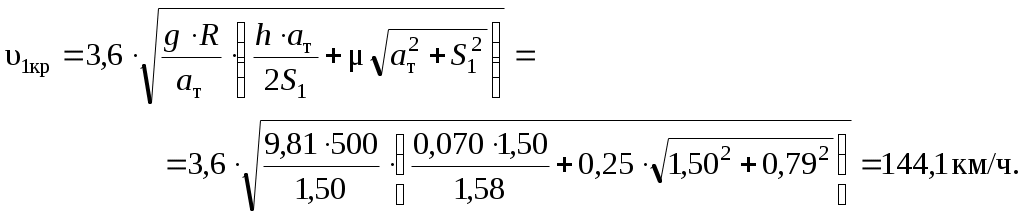 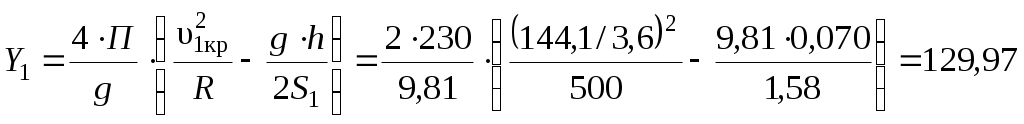 кН. кН. |
