Динамика эпс. Вариант 68. Исходные данные 4 расчет динамического паспорта тележки при движении

• Название: Исходные данные 4 расчет динамического паспорта тележки при движении
• Анкор: Динамика эпс
• Дата: 16.04.2022
• Размер: 1.13 Mb.
• Имя файла: Вариант 68.doc
• Тип: Реферат; #477588
• страница: 6 из 7

2ОЦЕНКА БЕЗОПАСНОСТИ ДВИЖЕНИЯ ЛОКОМОТИВА НА ПРЯМЫХ УЧАСТКАХ ПУТИ

2.1Расчет максимальной вертикальной нагрузки движущегося колеса

Расчетные параметры заданного типа верхнего строения пути приведены в таблице 2.1.
Таблица 2.1 – Расчетные параметры верхнего строения пути

Тип верхнего строения пути	Расчетные параметры
	U, МПа	кж, м-1	l, м	W, 10-3 м3	ω,м2	F, м2	β	γ
Р50(6)1840(II)П	21	1,085	0,55	0,273	0,0496	0,2734	1,0	1,5

На первом этапе расчета для каждого значения расчетной скорости определяем коэффициент вертикальной динамики:
(2.1)
где υ – расчетная скорость движения, км/ч;

∑f_ст – суммарный статический прогиб рессорного подвешивания, мм.

После этого определяем динамическую нагрузку на путь от колебаний надрессорного строения локомотива по формуле
. (2.2)
где П – нагрузка от одного колеса колесной пары на рельсы, Н;

М_н – неподрессоренная масса на одно колесо, т.

Среднее значение динамической нагрузки на путь от колебаний надрессорного строения и ее среднее квадратическое отклонение определяются по формулам
. (2.3)
. (2.4)
Суммарное среднее значение всех вертикальных динамических случайных нагрузок на путь определяется по формуле
. (2.5)
Среднее квадратическое отклонение динамической нагрузки от неровности пути для пути на деревянных шпалах рассчитывается по формуле
, (2.6)
где β – коэффициент, учитывающий тип рельса;

γ – коэффициент, учитывающий род балласта;

l – расстояние между осями смежных шпал, м;

U – модуль упругости рельсового основания. Па;

к_ж, – коэффициент относительной жесткости рельсового основания и рельсов, м^-1.

Среднее квадратическое отклонение динамической нагрузки на рельсы от влияния изолированной неровности на колесе определяется по формуле
(2.7)
где y_max – отношение наибольшего дополнительного прогиба рельса от действия указанной динамической нагрузки к глубине неровности колеса;

а₁ = 0,00047 м – глубина неровности колеса.

Величина y_max зависит от отношения Т_о/Т , где Т_о – время, в течение которого колесо проходит расстояние, равное длине неровности, а Т – период собственных, колебаний системы "колесо-рельс". Расчет выполняем в табличной форме (таблица 2.2) для значений скоростей, используемых в таблице 2.3.
Таблица 2.2 – Расчет отношения наибольшего прогиба рельса к глубине неровности

υ, км/ч	Параметр
	То′, с	То′′, с	Т, с	То′/Т	То′′/Т	ymax
20	0,036	0,707	0,071	0,50	9,88	1,47
30	0,024	0,471		0,34	6,59	1,47
40	0,018	0,353		0,25	4,94	1,47
50	0,014	0,283		0,20	3,95	1,47
60	0,012	0,236		0,17	3,29	1,47
70	0,010	0,202		0,14	2,82	1,47
80	0,009	0,177		0,13	2,47	1,47
90	0,008	0,157		0,11	2,20	1,47
100	0,007	0,141		0,10	1,98	1,47
110	0,007	0,128		0,09	1,80	1,47
120	0,006	0,118		0,08	1,65	1,47

Время прохождения колесом расстояния, равного длине неровности, определяем для крайних значений длины неровности по формулам
(2.8)
(2.9)
где D_к - заданный диаметр колеса колесной пары по кругу катания, м; υ - скорость движения, км/ч.

Период собственных колебаний системы "колесо-рельс" от скорости движения не зависит и определяется по формуле
(2.10)
где параметры к_ж, М_н и U имеют размерность м^-1, т и Па соответственно. Если выполняется неравенство
Т_о′/Т < 0,71 < Т_о′′/Т, (2.11)
то y_max принимаем равным 1,47. Если неравенство (2.11) не выполняется, то для определения y_max используем зависимость y_max = f(Т_о/Т), приведенную в [1]. В этом случае по указанной зависимости определяем значение у₁, соответствующее отношению Т_о′/Т, и значение у₂, соответствующее отношению Т_о′′/Т. Из двух значений у₁, и у₂ выбираем наибольшее, приняв его за y_max.

Среднее квадратическое отклонение динамической нагрузки на рельсы от влияния непрерывной неровности на колесе определяем по формуле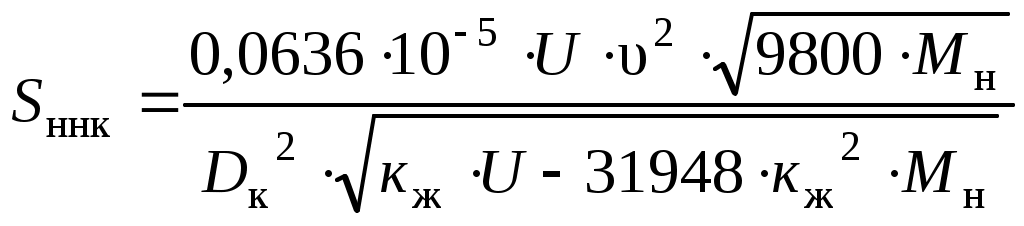
, (2.12)
где параметры U, υ, М_н, D_к, к_ж, имеют размерность Па, км/ч, т, м, м^-1 соответственно.

Для пути на деревянных шпалах суммарное среднее квадратическое отклонение всех составляющих динамических нагрузок на рельсы определяем по формуле
. (2.13)
Величину максимальной вертикальной нагрузки движущегося колеса в предположении нормального закона распределения случайных составляющих динамических нагрузок рассчитываем по формуле
. (2.14)
Примеры расчетов:

Приведем пример расчетов для скорости 20 км/ч

Определяем коэффициент вертикальной динамики:



Находим динамическую нагрузку на путь от колебаний надрессорного строения:

Н.

Среднее значение динамической нагрузки от колебаний надрессорного строения:



Среднее квадратическое отклонение этой нагрузки:



Находим суммарное среднее значение вертикальных динамических нагрузок на путь:



Определим среднее квадратическое отклонение динамической нагрузки от влияния случайной неровности пути: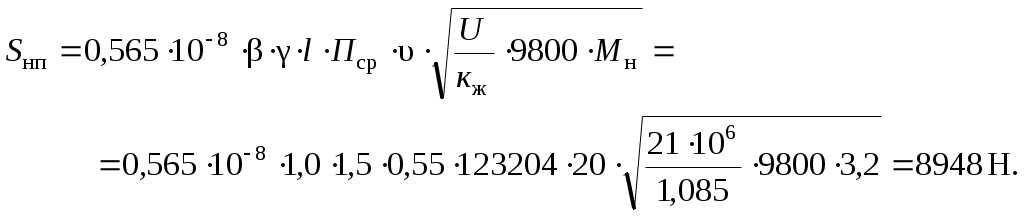



Рассчитаем время прохождения колесом расстояния, равного длине неровности:





Найдем период собственных колебаний системы "колесо-рельс":



.

Т.к. выполняется условие Т_о′/Т < 0,71 < Т_о′′/Т, принимаемy_max = 1,47.

Среднее квадратическое отклонение динамической нагрузки на рельсы от влияния изолированной неровности на колесе равно:



Определим среднее квадратическое отклонение случайной динамической нагрузки на рельсы от влияния непрерывной неровности на колесе: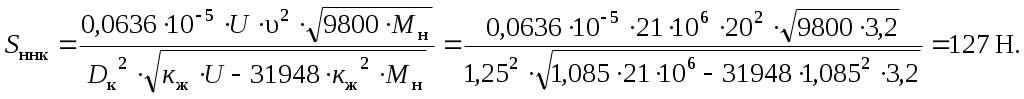



Найдем среднее квадратическое отклонение всех составляющих динамических нагрузок на рельсы: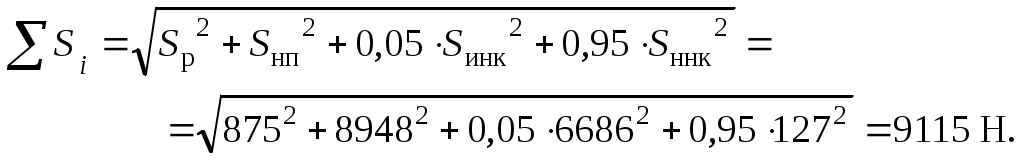



Определим максимальную вертикальную нагрузку движущегося колеса



Результаты расчетов сведены в таблице 2.3.
Таблица 2.3 – Результаты расчета максимальной вертикальной нагрузки движущегося колеса

υ, км/ч	Параметр
	кд	Пр, Н	Sр, Н	Пср, Н	Sнп, Н	Sинк, Н	Sннк, Н	ΣSi, Н	Пmax, Н
20	0,131	10938	875	123204	8948	6686	127	9115	145992
30	0,146	12224	978	124168	13527	6686	286	13647	158286
40	0,162	13511	1081	125133	18177	6686	509	18277	170826
50	0,177	14798	1184	126099	22896	6686	795	22988	183569
60	0,192	16085	1287	127064	27686	6686	1145	27779	196512
70	0,208	17371	1390	128028	32545	6686	1558	32644	209638
80	0,223	18658	1493	128994	37475	6686	2035	37587	222962
90	0,238	19945	1596	129959	42475	6686	2575	42605	236472
100	0,254	21232	1699	130924	47545	6686	3180	47700	250174
110	0,269	22518	1801	131889	52685	6686	3847	52870	264064
120	0,285	23805	1904	132854	57895	6686	4579	58117	278147