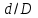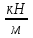Спромат задачи. Сопромат задачи. Исходные данные для расчетов
 Скачать 343.7 Kb. Скачать 343.7 Kb.
|
|
Исходные данные для расчетов.
Задача 1. РАСЧЕТ СТУПЕНЧАТОГО БРУСА НА РАСТЯЖЕНИЕ–СЖАТИЕ (Тема: «Центральное растяжение-сжатие». Раздел: «Статически определимые системы».) Для ступенчатого стального бруса круглого поперечного сечения, (рис. 1), выполненного из стали марки Ст. 3, имеющей предел текучести sТ, модуль Юнга E, требуется: 1) построить по длине бруса эпюры продольных сил N, нормальных напряжений s и перемещений поперечных сечений d; 2) вычислить коэффициент запаса прочности бруса n. Принять: а = 0,1ℓ1; в = 0,1ℓ2; с = 0,1ℓ3. 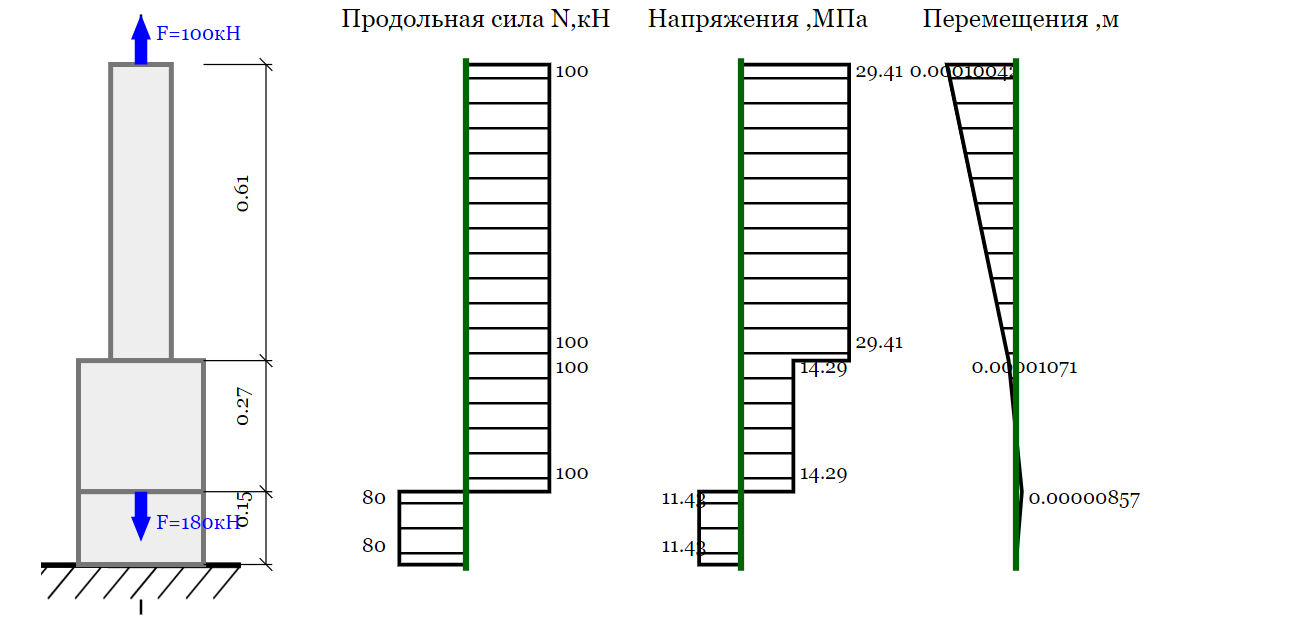 Определим продольные силы на участках стержня, начиная с верхнего N1 = + 100 = 100кН N2 = + 100 = 100кН N3 = + 100 - 180 = -80кН Напряжения равны продольной силе, деленной на площадь σ1 = 100000/3400=29.41 МПа σ2 = 100000/7000=14.29 МПа σ3 = -80000/7000=-11.43 МПа Удлинения участков определяем по закону Гука, учитывая продольную силу N, кН, длину l, м, площадь А, мм2 и модуль упругости материала E, МПа Δl = N×l/E×A Δl1 = 100000 × 0.61 / (200000 × 3400) = 8.971E-5м Δl2 = 100000 × 0.27 / (200000 × 7000) = 1.929E-5м Δl3 = -80000 × 0.15 / (200000 × 7000) = -8.57E-6м Удлинение всего стержня равно сумме удлинений его участков Δl = + 8.971E-5 + 1.929E-5 - 8.57E-6 = 0.0001 м Коэффициент запаса прочности n=160/29.41=5.44 Задача 3. ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК ПЛОСКИХ СЕЧЕНИЙ (Тема: «Геометрические характеристики плоских сечений».) Задано поперечное сечение, состоящее из двух профилей, имеющих вид швеллера, двутавра или равнополочного уголка (рис. 3), Требуется: 1) определить положение центра тяжести поперечного сечения; 2) найти осевые и центробежный моменты инерции относительно случайных осей (xC и yC), проходящих через центр тяжести; 3) определить положение главных центральных осей u и v; 4) найти моменты инерции относительно главных центральных осей; 5) вычертить сечение и указать на нем все размеры в числах и все оси. При расчете все необходимые данные следует брать из таблиц сортамента.  Площадь сечения Суммарную площадь фигуры вычислим по формуле: A = A1 + A2 + A3 где: A1 - площадь швеллера №1, A2 - площадь швеллера №2, A3 - площадь уголка №3. A1 = 26.71 (см2) – данные получены из справочника: Швеллеры с параллельными гранями полок по ГОСТ 8240-97 = 26.71 (см2) – данные получены из справочника: Швеллеры с параллельными гранями полок по ГОСТ 8239-89 A2 = 26.71 (см2) – данные получены из справочника: Швеллеры с параллельными гранями полок по ГОСТ 8240-97 = 26.71 (см2) – данные получены из справочника: Швеллеры с параллельными гранями полок по ГОСТ 8239-89 A3 = 19.69 (см2) – данные получены из справочника: Уголки равнополочные по ГОСТ 8509-86 = 19.69 (см2) – данные получены из справочника: Уголки равнополочные по ГОСТ 8509-86 Получим, A = 26.71 + 26.71 + 19.69 = 73.11 (см2) Статические моменты Обозначим начало координат в самой левой нижней точке сечения. Тогда статический момент сложной фигуры относительно оси Ox равен сумме статических моментов простых фигур составляющих эту фигуру. Sx = Sx(1) + Sx(2) + Sx(3) где Sx(1) - статический момент швеллера №1 отн. оси Ox; Sx(2) - статический момент швеллера №2 отн. оси Ox; Sx(3) - статический момент уголка №3 отн. оси Ox. Sx(1) = A1 × yc(1) = 26.71 × 11 = 293.81 (см3) Sx(2) = A2 × yc(2) = 26.71 × 11 = 293.81 (см3) Sx(3) = A3 × yc(3) = 19.69 × 25.36 = 499.338 (см3) где yc(1) - расстояние от центра тяжести швеллера №1 до оси Ox (по оси Oy), yc(2) - расстояние от центра тяжести швеллера №2 до оси Ox (по оси Oy), yc(3) - расстояние от центра тяжести уголка №3 до оси Ox (по оси Oy). Получим, Sx = 293.81 + 293.81 + 499.338 = 1086.958 (см3) Статический момент сложной фигуры относительно оси Oy равен сумме статических моментов простых фигур составляющих эту фигуру. Sy = Sy(1) + Sy(2) + Sy(3) где Sy(1) - статический момент швеллера №1 отн. оси Oy; Sy(2) - статический момент швеллера №2 отн. оси Oy; Sy(3) - статический момент уголка №3 отн. оси Oy. Sy(1) = A1 × xc(1) = 26.71 × 14.97 = 399.849 (см3) Sy(2) = A2 × xc(2) = 26.71 × 9.98 = 266.566 (см3) Sy(3) = A3 × xc(3) = 19.69 × 9.14 = 179.967 (см3) где xc(1) - расстояние от центра тяжести швеллера №1 до оси Oy (по оси Ox), xc(2) - расстояние от центра тяжести швеллера №2 до оси Oy (по оси Ox), xc(3) - расстояние от центра тяжести уголка №3 до оси Oy (по оси Ox). Получим, Sy = 399.849 + 266.566 + 179.967 = 846.381 (см3) Центр тяжести Зная площадь сечения и его статические моменты можно определить координаты центра тяжести по следующим формулам: xc = Sy/A = 846.381 / 73.11 = 11.58 (см) yc = Sx/A = 1086.958 / 73.11 = 14.87 (см) Значения координат получены относительно выбранного начала координат O. На схеме центр тяжести обозначен точкой С. 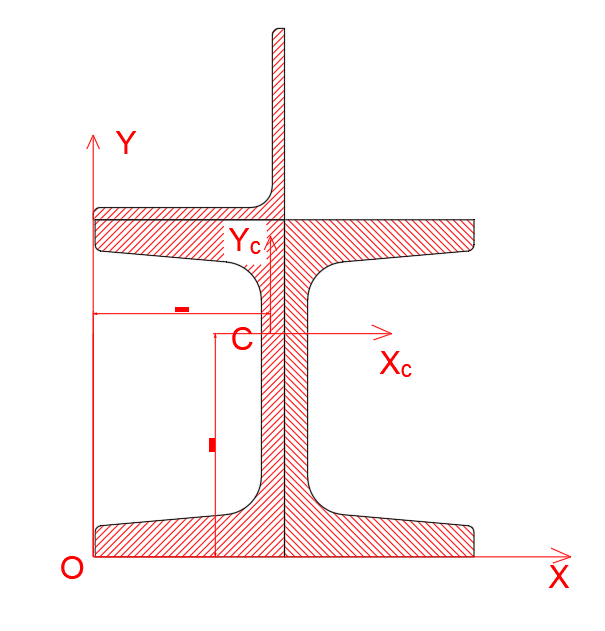 Моменты инерции Моменты инерции будем вычислять относительно центральных осей фигуры (центра тяжести). Ixс = Ixс(1) + Ixс(2) + Ixс(3) где: Ixc(1) - осевой центральный момент инерции швеллера №1 отн. оси Xc; Ixc(2) - осевой центральный момент инерции швеллера №2 отн. оси Xc; Ixc(3) - осевой центральный момент инерции уголка №3 отн. оси Xc. Вычислим осевой центральный момент инерции швеллера №1 отн. оси Xc по формуле: Ixc(1) = I'x(1) + y12 × A1 где: I'x(1) - осевой момент инерции швеллера №1 относительно собственного центра тяжести, y1 - расстояние от центра тяжести швеллера №1 до оси Xc (по оси Yc); I'x(1) = 2117.9 (см4) – данные получены из справочника: Швеллеры с параллельными гранями полок по ГОСТ 8240-97 Ixc(1) = 2117.9 + (14.867 - 11)2 × 26.71 = 2517.404 (см4) Вычислим осевой центральный момент инерции швеллера №2 отн. оси Xc по формуле: Ixc(2) = I'x(2) + y22 × A2 где: I'x(2) - осевой момент инерции швеллера №2 относительно собственного центра тяжести, y2 - расстояние от центра тяжести швеллера №2 до оси Xc (по оси Yc); I'x(2) = Ix(2) × cos2(α) + Iy(2) × sin2(α) - Ixy(2) × sin(2 × α), где: Ix(2) = 2117.9 (см4), Iy(2) = 177.92 (см4), Ixy(2) = 0 (см) – данные получены из справочника: Швеллеры с параллельными гранями полок по ГОСТ 8240-97 I'x(2) = 2117.9 × cos2(-180) + 177.92 × sin2(-180) - 0 × sin(2 × -180) = 2117.9 (см4) Ixc(2) = 2117.9 + (14.867 - 11)2 × 26.71 = 2517.404 (см4) Вычислим осевой центральный момент инерции уголка №3 отн. оси Xc по формуле: Ixc(3) = I'x(3) + y32 × A3 где: I'x(3) - осевой момент инерции уголка №3 относительно собственного центра тяжести, y3 - расстояние от центра тяжести уголка №3 до оси Xc (по оси Yc). I'x(3) = Ix(3) × cos2(α) + Iy(3) × sin2(α) - Ixy(3) × sin(2 × α), где: Ix(3) = 294.36 (см4), Iy(3) = 294.36 (см4), Ixy(3) = 0 (см) – данные получены из справочника: Уголки равнополочные по ГОСТ 8509-93 I'x(3) = 294.36 × cos2(90) + 294.36 × sin2(90) - 0 × sin(2 × 90) = 294.36 (см4) Ixc(3) = 294.36 + (25.36 - 14.867)2 × 19.69 = 2462.108 (см4) Получим, Ixc = 2517.404 + 2517.404 + 2462.108 = 7496.915 (см4) Iyс = Iyс(1) + Iyс(2) + Iyс(3) где: Iyc(1) - осевой центральный момент инерции швеллера №1 отн. оси Yc; Iyc(2) - осевой центральный момент инерции швеллера №2 отн. оси Yc; Iyc(3) - осевой центральный момент инерции уголка №3 отн. оси Yc. Вычислим осевой центральный момент инерции швеллера №1 отн. оси Yc по формуле: Iyc(1) = I'y(1) + x12 × A1 где: I'y(1) - осевой момент инерции швеллера №1 относительно собственного центра тяжести, x1 - расстояние от центра тяжести швеллера №1 до оси Yc (по оси Xc); I'y(1) = 177.92 (см4) – данные получены из справочника: Швеллеры с параллельными гранями полок по ГОСТ 8240-97 Iyc(1) = 177.92 + (14.97 - 11.577)2 × 26.71 = 485.451 (см4) Вычислим осевой центральный момент инерции швеллера №2 отн. оси Yc по формуле: Iyc(2) = I'y(2) + x22 × A2 где: I'y(2) - осевой момент инерции швеллера №2 относительно собственного центра тяжести, x2 - расстояние от центра тяжести швеллера №2 до оси Yc (по оси Xc); I'y(2) = Ix(2) × sin2(α) + Iy(2) × cos2(α) + Ixy(2) × sin(2 × α), где: Ix(2) = 2117.9 (см4), Iy(2) = 177.92 (см4), Ixy(2) = 0 (см) – данные получены из справочника: Швеллеры с параллельными гранями полок по ГОСТ 8240-97 I'y(2) = 2117.9 × sin2(-180) + 177.92 × cos2(-180) + 0 × sin(2 × -180) = 177.92 (см4) Iyc(2) = 177.92 + (11.577 - 9.98)2 × 26.71 = 246.026 (см4) Вычислим осевой центральный момент инерции уголка №3 отн. оси Yc по формуле: Iyc(3) = I'y(3) + x32 × A3 где: I'y(3) - осевой момент инерции уголка №3 относительно собственного центра тяжести, x3 - расстояние от центра тяжести уголка №3 до оси Yc (по оси Xc). I'y(3) = Ix(3) × sin2(α) + Iy(3) × cos2(α) + Ixy(3) × sin(2 × α), где: Ix(3) = 294.36 (см4), Iy(3) = 294.36 (см4), Ixy(3) = 0 (см) – данные получены из справочника: Уголки равнополочные по ГОСТ 8509-93 I'y(3) = 294.36 × sin2(90) + 294.36 × cos2(90) + 0 × sin(2 × 90) = 294.36 (см4) Iyc(3) = 294.36 + (11.577 - 9.14)2 × 19.69 = 411.281 (см4) Получим, Iyc = 485.451 + 246.026 + 411.281 = 1142.757 (см4) Моменты сопротивления Осевым моментом сопротивления площади сечения относительно главной центральной оси называется отношение момента инерции площади относительно этой же оси к расстоянию до наиболее удаленной точки от этой оси. Wxс = Ixс/ymax = 7496.915/14.867 = 504.251 (см3) Wyс = Iyс/xmax = 1142.757/11.577 = 98.711 (см3) Задача 4. РАСЧЕТ ВАЛА НА КРУЧЕНИЕ Стальной вал, закручивается двумя моментами m1 и m2 (рис. 4). Два участка вала имеют форму поперечного сечения в виде кругов диаметрами d1 и d2, а третий участок вала полый - имеет форму поперечного сечения в виде кольца с заданным отношением внутреннего диаметра d к наружному D. Требуется: 1) построить эпюру крутящих моментов МК; 2) из условия прочности по допускаемым касательным напряжениям [τ] определить размеры поперечных сечений участков вала и округлить их до ближайшей большей величины в мм; 3) построить эпюру углов поворота α. Принять: а = 0,1ℓ3. 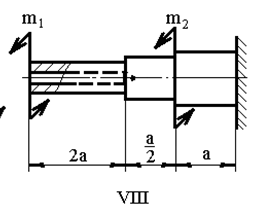 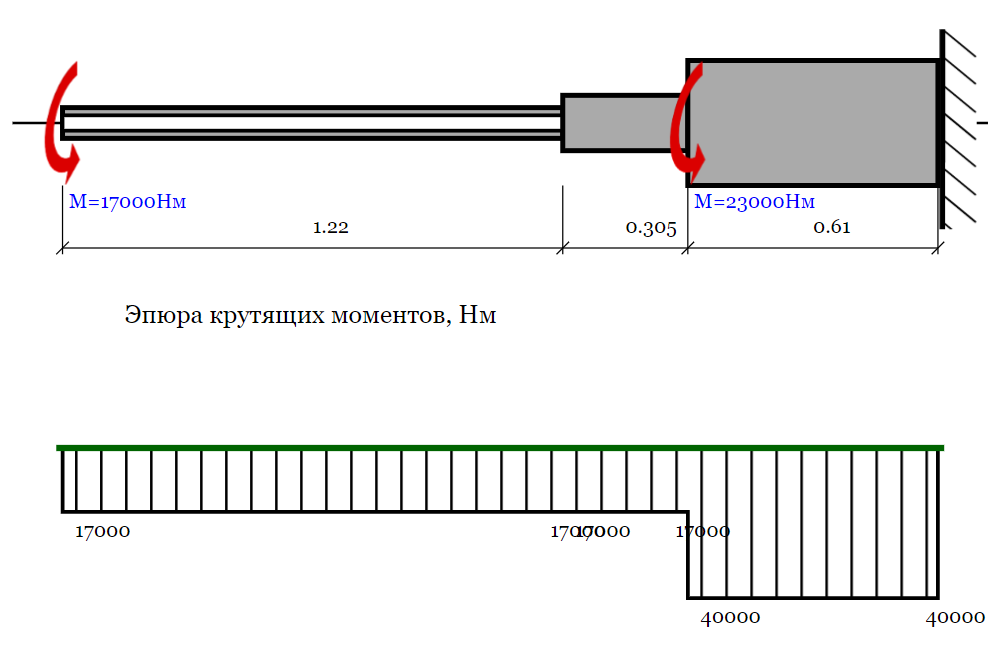 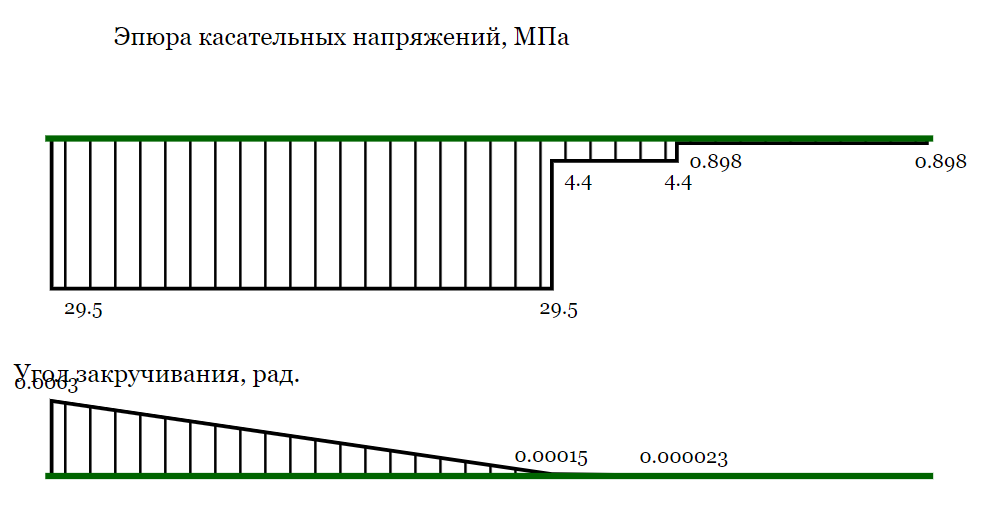 Моменты инерции сечений вала Jk1 = π×d4×(1-α4)/32 = π×154×(1-0.64)/32 = 4324 см4 Jk2 = π×d4/32 = π×274/32 = 52150 см4 Jk3 = π×d4/32 = π×614/32 = 1359000 см4 Моменты сопротивления сечений вала Wk1 = π×d3×(1-α4)/16 = π×153×(1-0.64)/16 = 577 см3 Wk2 = π×d3/16 = π×273/16 = 3863 см3 Wk3 = π×d3/16 = π×613/16 = 44550 см3 Моменты на участках вала определяем, используя метод сечений - первый участок M1 = -17000 = -17000Нм - второй участок M2 = -17000 = -17000Нм - третий участок M3 = -17000 -23000 = -40000Нм Угол закручивания на одном участке определяется по формуле ϕ=M∗l/G∗Jk - первый участок φ1 = -17000×1.22 / 78000×106×4324×10-8 = -0.006149 рад - второй участок φ2 = -17000×0.305 / 78000×106×52150×10-8 = -0.0001275 рад - третий участок φ3 = -40000×0.61 / 78000×106×1359000×10-8 = -2.302E-5 рад По полученным данным строим эпюры. Эпюру углов закручивания строим, начиная с правого закрепленного конца вала. Задача 5.РАСЧЕТ ШАРНИРНО-ОПЕРТОЙ БАЛКИ НА ИЗГИБ (Тема: «Изгиб».) Стальная балка, изображена на рис. 5. Требуется: 1) построить эпюры поперечной силы QУ и изгибающего момента МХ; 2) подобрать из условия прочности по допускаемым напряжениям поперечные сечения в виде круга, квадрата, двутавра и двух швеллеров; 3) сравнить принятые сечения балок по экономичности. Стенки двутавра и двух швеллеров параллельны действующей нагрузке. Принять: F = F1 ; m = m1. 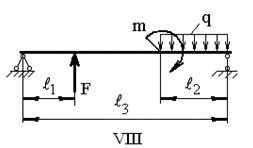 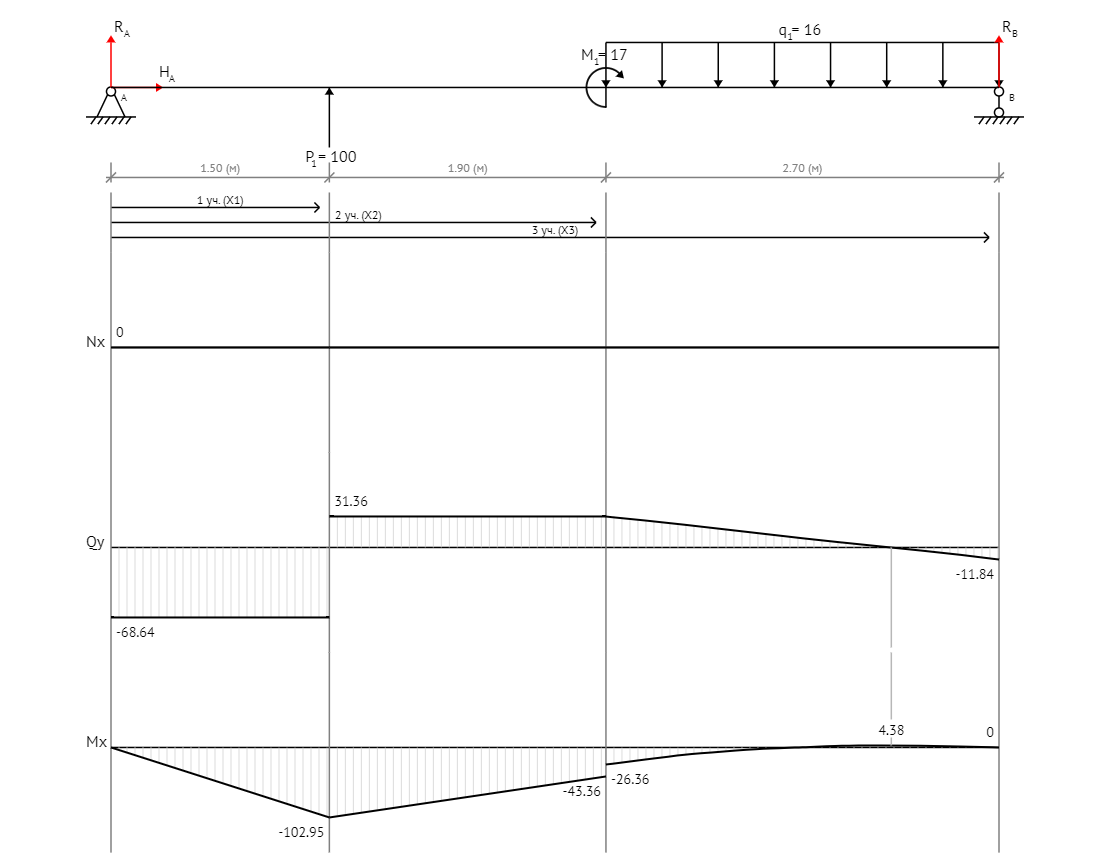 Рис.1 — Расчетная схема балки Определение опорных реакций 1) Согласно схеме решения задач статики определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки. 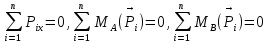 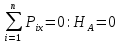 Найдем сумму моментов относительно шарнирно-неподвижной опоры в точке A: 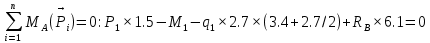 Найдем сумму моментов относительно шарнирно-подвижной опоры в точке B: 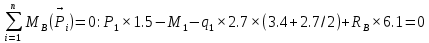 2) Вычислим реакцию шарнирно-подвижной опоры в точке B: 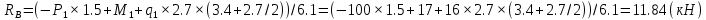 Так как реакция отрицательна, на расчетной схеме направим ее в противоположную сторону. 3) Вычислим реакцию шарнирно-неподвижной опоры в точке A: 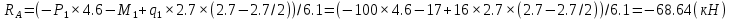 4) Решаем полученную систему уравнений, находим неизвестные: 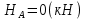 5) Выполним проверку решения, подставляя найденные значения в уравнение равновесия относительно оси Oy: 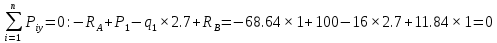 Построение эпюр 1) Рассмотрим первый участок 0 ≤ x1 < 1.5 Продольная сила N: 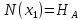 Значения N на краях участка: 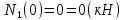 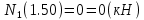 Поперечная сила Q: 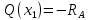 Значения Q на краях участка: 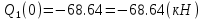 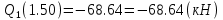 Изгибающий момент M: 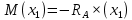 Значения M на краях участка: 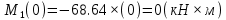 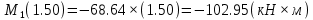 2) Рассмотрим второй участок 1.5 ≤ x2 < 3.4 Продольная сила N: 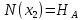 Значения N на краях участка: 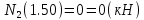 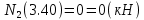 Поперечная сила Q: 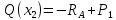 Значения Q на краях участка: 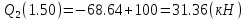 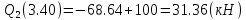 Изгибающий момент M: 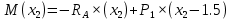 Значения M на краях участка: 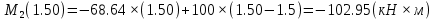 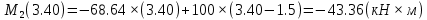 3) Рассмотрим третий участок 3.4 ≤ x3 < 6.1 Продольная сила N: 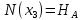 Значения N на краях участка: 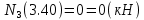 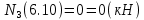 Поперечная сила Q: 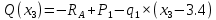 Значения Q на краях участка: 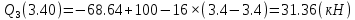 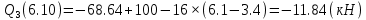 На этом участке эпюра Q пересекает горизонтальную ось. Точка пересечения: x = 1.96. Изгибающий момент M: 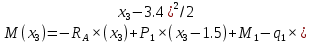 Значения M на краях участка: 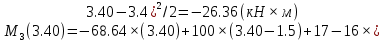 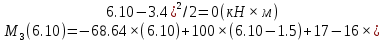 Локальный экстремум в точке x = 1.96: 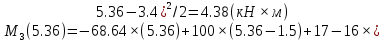 Вычисляем размеры сечения данной балки из условий прочности на изгиб 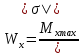 Прямоугольное 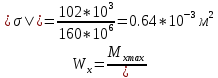 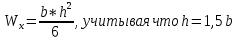 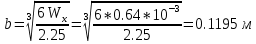 Круглое сечение: 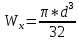 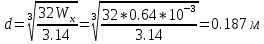 Швеллер: 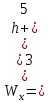 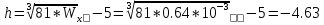 – не проходит сечение – не проходит сечение Швеллер: 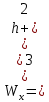 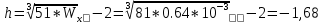 не проходит сечение. не проходит сечение.Задача 6. РАСЧЕТ БАЛКИ-КОНСОЛИ НА ИЗГИБ (Тема: «Изгиб».) Стальная балка, изображена на рис. Требуется: 1) построить эпюры поперечной силы QУ и изгибающего момента МХ; 2) подобрать из условия прочности по допускаемым напряжениям сложное поперечное сечение, изображенное справа от схемы балки. Принять: F = F1; m = m1. 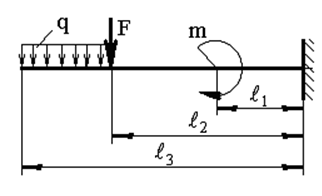 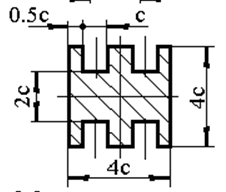 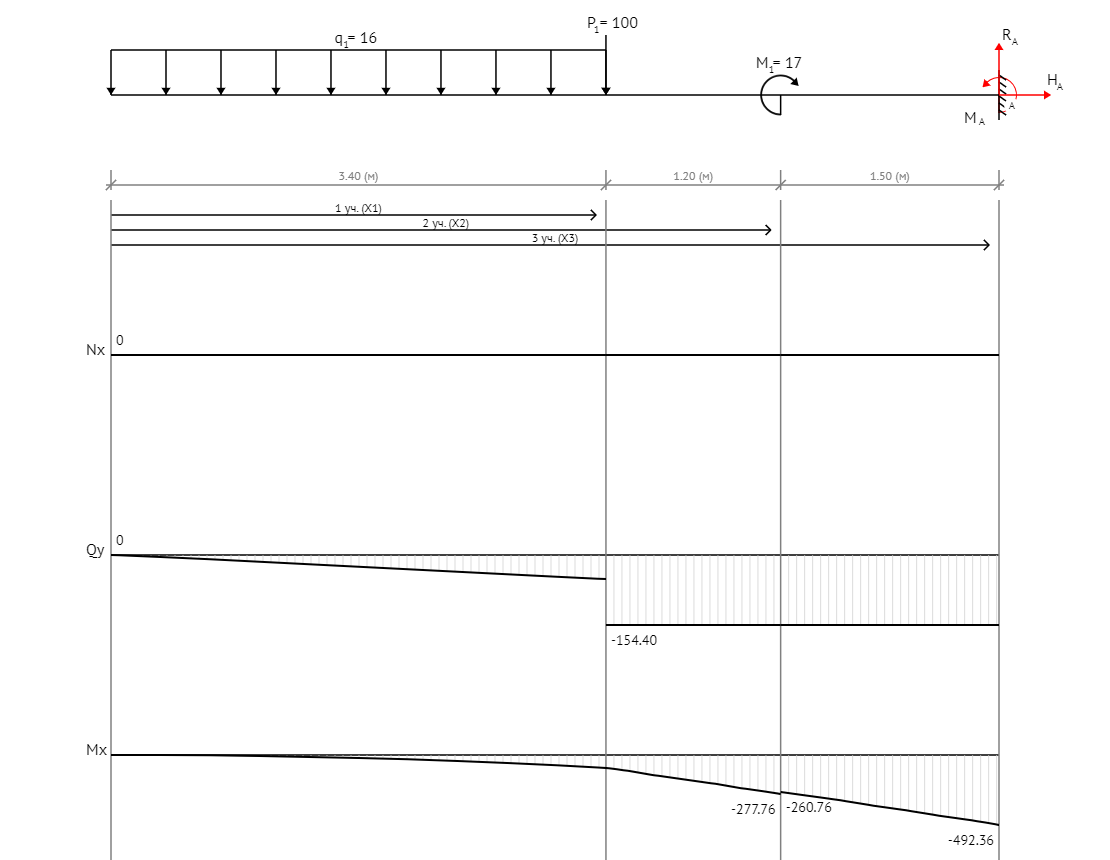 Рис.1 — Расчетная схема балки Определение опорных реакций Согласно схеме решения задач статики определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки. 1) На балку наложена связь в точке A (справа) типа жесткая заделка, поэтому освобождаем балку, заменив действие связи реакциями (HA, RA, MA). 2) Определим реакции опор в соответствии с уравнениями равновесия балки: 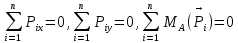 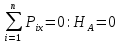 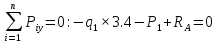 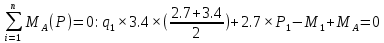 3) Решаем полученную систему уравнений, находим неизвестные: 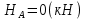 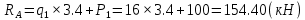 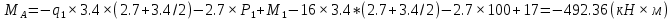 Так как момент отрицателен, на расчетной схеме направим его в противоположную сторону. 4) Выполним проверку, составив дополнительное моментное уравнение относительно свободного конца балки: 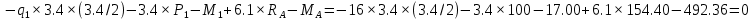 Построение эпюр 1) Рассмотрим первый участок 0 ≤ x1 < 3.4 Продольная сила N: 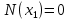 Значения N на краях участка: 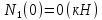 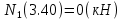 Поперечная сила Q: 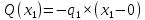 Значения Q на краях участка: 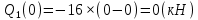 Изгибающий момент M: 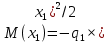 Значения M на краях участка: 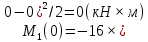 2) Рассмотрим второй участок 3.4 ≤ x2 < 4.6 Продольная сила N: 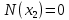 Значения N на краях участка: 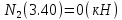 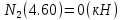 Поперечная сила Q: 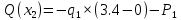 Значения Q на краях участка: 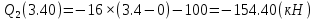 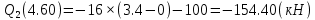 Изгибающий момент M: 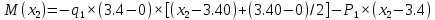 Значения M на краях участка: 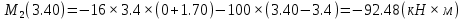 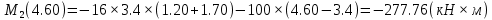 3) Рассмотрим третий участок 4.6 ≤ x3 < 6.1 Продольная сила N: 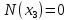 Значения N на краях участка: 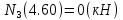 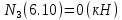 Поперечная сила Q: 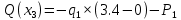 Значения Q на краях участка: 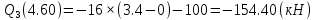 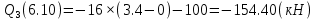 Изгибающий момент M: 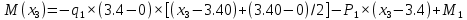 Значения M на краях участка: 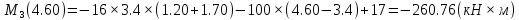 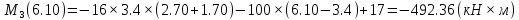 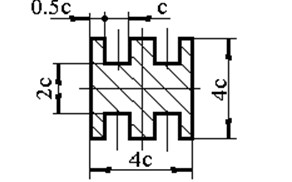 Подбор сечения. Подбор сечения.Воспользуемся отношением: 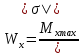 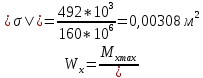 Для нашего сечения : 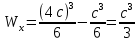 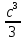 = =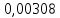 , ,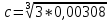 =0.209 м =0.209 м |