Исходные данные Расчет соединений путей
 Скачать 453.2 Kb. Скачать 453.2 Kb.
|
 Содержание СодержаниеСтр Исходные данные……………………………………………………………..3 1. Расчет соединений путей.……….....………………………………….…...4 Одиночное соединение с искривлением одного пути………....……….4 2. Расчет длин съездов...................................................................…………...6 2.1 Несокращенный съезд………………………………………………….....6 2.2 Перекрестный съезд………………………………………………………8 3. Стрелочные улицы.……….......................................................………..…. 9 3.1 Простейшая стрелочная улица под углом крестовины.………....…......9 3.2 Простейшая стрелочная улица на основном пути..………...………....12 4. Раздвижка путей…………………………………………………………..14 5. Эпюра стрелочного перевода…………………………………………….17 Приложение А…………………………………………………………….18 Приложение Б……………………………………………………………..19 Приложение В……………………………………………………………..20 Исходные данные: Марка крестовины 1/11; Тип рельс Р65; Угол крестовины α=5º11'40"; Междупутье Е=5,3 м; Уширение междупутья Еуш=7,5 м; Геометрические элементы СП: Расстояние: от передних стыков рамного рельса до центра стрелочного перевода а=14,059 м; от центра стрелочного перевода до начала остряков а0=11,294 м; от центра стрелочного перевода до задних стыков крестовины b=20,795 м; от центра стрелочного перевода до математического центра b0=16,754 м; от стыка рамного рельса до начала остряка m=2,765 м; от математического центра стрелочного перевода до задних стыков крестовины q=4,198 м; Длина стрелочного перевода Lп=34,854 м; Радиус закрестовинной кривой R=300 м; Тригонометрические функции угла крестовины sinα = sin(5º11'40") = 0,090536; cosα = cos(5º11'40") = 0,995893; tgα = tg(5º11'40") = 0,090909. 1. Расчет соединений путей 1.1 Одиночное конечное соединение с искривлением одного пути Рассчитать одиночное конечное соединение приемоотправочных путей в нормальных условиях с искривлением одного пути. Расстояние между осями путей Е=5,30 м Радиус сопрягаемой прямой R=300 м. 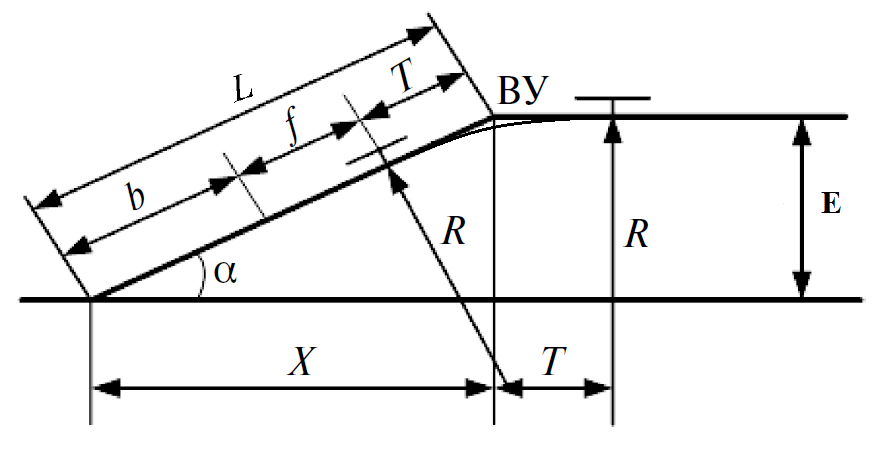 Рисунок 1.1 – Одиночное конечное соединение приемоотправочных путей Решение: Координаты вершины угла поворота вычисляют по формулам: x= 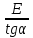 (1) (1)y=Е (2) где Е – ширина междупутья, м; α – угол крестовины; х= 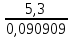 =58,3 м =58,3 му=5,3 м Расстояние от начала или конца кривой до вершины угла поворота (Тангенс кривой) вычисляют по формуле: T=R∙tg 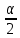 (3) (3)где Т – тангенс кривой, м; R – радиус переводной кривой, м; α – угол крестовины; Т=300∙tg 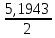 =13,608 м =13,608 мДлину кривого участка пути вычисляют по формуле: K= 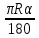 (4) (4)где К – длинна кривого участка пути, м; R – радиус переводной кривой, м; 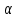 – угол поворота; – угол поворота; К=3,14∙300∙5,1943/180=27,184 м Длину вставки между концами стрелочного перевода и началом кривой вычисляют по формуле: ƒ = 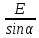 - (b+T) (5) - (b+T) (5)где ƒ – длина вставки между концами стрелочного перевода и началом кривой, м; Е – ширина междупутья, м; α – угол крестовины; b – расстояние от центра стрелочного перевода до задних стыков крестовины, м; Т – тангенс кривой, м; f=58,54- (20,795+13,608)=24,137 м. Конечное соединение в масштабе приведено в Приложении А. 2. Расчет длин съездов 2.1 Несокращенный съезд Рассчитать не сокращенный съезд между двумя параллельными путями. 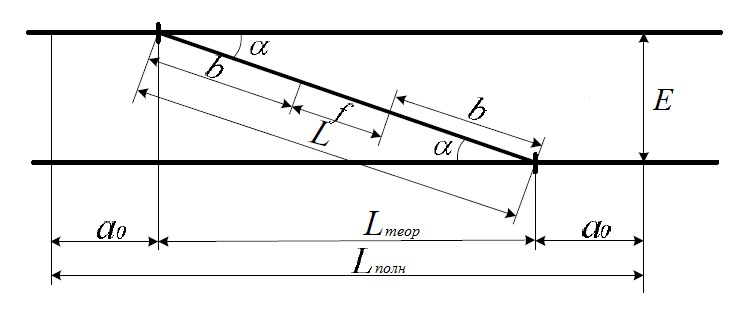 Рисунок 2 - Съезд Решение: Из прямоугольного треугольника определяем расстояние между центрами стрелочных переводов (проектируемое на горизонтальную ось) по формуле (1) : Lтеор= Е/tgα Lтеор= 5,3/0,090909=58,3 м Из прямоугольного треугольника АВС определяем расстояние между центрами стрелочных переводов по формуле: L= Е/sinα (16) где Е – ширина междупутья, м; α – угол крестовины; L=5,3/0,090536= 58,54 м Полную длину съезда вычисляют по формуле: Lполн=Lтеор+a+а=Е/tgα+2a (17) где Lтеор – расстояние между центрами стрелочных переводов, проектируемое на горизонтальную ось, м; а – расстояние от центра стрелочного перевода до стыка рамных рельс, м; Lполн= 58,3+2*14,059= 86,418 м Длина вставки между концами стрелочного перевода и началом кривой вычисляют по формуле: ƒ = Е/sinα – ( b+b) (18) где ƒ – длина вставки между концами стрелочного перевода и началом кривой, м; Е – ширина междупутья, м; α – угол крестовины; b – расстояние от центра стрелочного перевода до задних стыков крестовины, м; ƒ =5,3/0,090536-(20,795+20,795)=16,95 м. Съезд в масштабе приведен в Приложении А. 2.2 Перекрестный съезд Рассчитать длину перекрестного съезда. 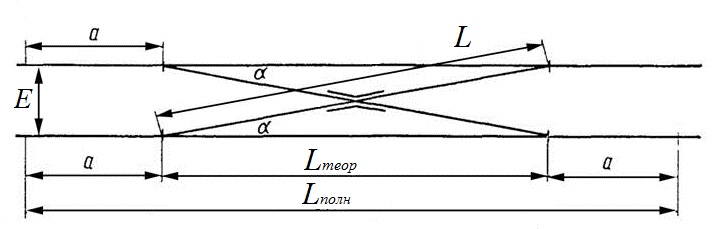 Рисунок 2.2 – Перекрестный съезд Решение: Из прямоугольного треугольника определяем расстояние между центрами стрелочных переводов (проектируемое на горизонтальную ось) по формуле (1): Lтеор= Е/tgα Lтеор= 5,3/0,090909=58,3 м Из прямоугольного треугольника определяем расстояние между центрами стрелочных переводов по формуле (16): L=Е/sinα L=5,3/0,090536= 58,3 м Полную длину съезда вычисляют по формуле (17): Lполн=Lтеор+a+а=Е/tgα+2a Lполн = 58,3+2*14,059= 86,418 м Длина вставки между концами стрелочного перевода и началом кривой вычисляют по формуле (18): ƒ = Е/sinα – (b+b) ƒ =5,3/0,110433-(15.85+15.85)=16,3 м Перекрестный съезда в масштабе приведен Приложении Б. 3. Стрелочные улицы 3.1.Простейшая стрелочная улица под углом крестовины Рассчитываем простейшую стрелочную улицу под углом крестовины на путях отстоя пассажирских вагонов. Приняв центр стрелочного перевода за начало координат, и, проектируя на горизонтальную и вертикальную оси, определяем расстояние. 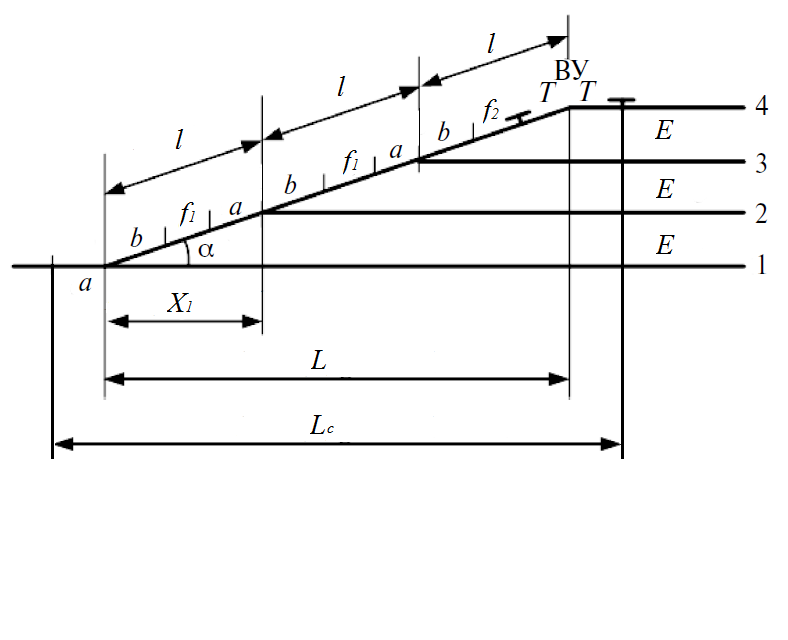 Рисунок 3.1 – Простейшая стрелочная улица под углом крестовины Решение: Координаты центров стрелочных переводов вычисляют по формулам (1) и (2), последовательно прибавляя предыдущие значения: 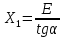 нет нумерации формул справой стороны нет нумерации формул справой стороны    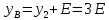 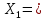 5,3/0,090536=58,3 м 5,3/0,090536=58,3 м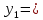 5,3 м 5,3 м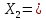 58,3+5,3/0,090536=116,6 м 58,3+5,3/0,090536=116,6 м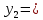 2*5,3=10,6 м 2*5,3=10,6 м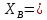 116,6+5,3/0,090536=174,9 м 116,6+5,3/0,090536=174,9 м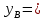 3*5,3=15,9 м 3*5,3=15,9 мРасстояние от начала или конца кривой до вершины угла поворота (Тангенс кривой) вычисляют по формуле (3): 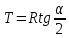 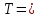 300*0,045359=13,608 м 300*0,045359=13,608 мДлину кривого участка пути вычисляют по формуле (4): 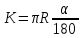 К = 3,14∙300∙5,1943/180=27,184 м Длину вставки между концами стрелочного перевода и началом кривой вычисляют по формуле (5): 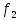 = Е/sinα- (b+Т) = Е/sinα- (b+Т) 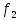 =5,3/0,090536-(20,795+13,608)=24,137 =5,3/0,090536-(20,795+13,608)=24,137Длину вставки между концами одного стрелочного перевода и началом другого, вычисляют по формуле: 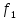 =Е/sinα– (b+a) (19) =Е/sinα– (b+a) (19)где 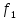 – длина вставки между концами одного стрелочного перевода и началом другого, м; – длина вставки между концами одного стрелочного перевода и началом другого, м;Е – ширина междупутья, м; α – угол крестовины; b – расстояние от центра стрелочного перевода до задних стыков крестовины, м; а – расстояние от центра стрелочного перевода до стыка рамных рельс, м; 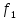 =58,54-(20,795+14,059)=23,69 м =58,54-(20,795+14,059)=23,69 мРасстояние между центрами стрелочных переводов вычисляют по формуле (16): l=Е/sinα l = 5,3/0,090536= 58,54 м. Длину стрелочной улицы (проекцию на горизонтальную ось) от центра перевода до вершины угла поворота крайнего пути вычисляют по формуле: 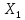 = Е/tgα = Е/tgα L=∑Е/tgα (20) ∑Е=Е*(n-1) где Е – ширина междупутья, м; n – количество путей в стрелочной улице; α – угол крестовины; L =(5,3+5,3+5,3)/0,090909=174,9 м. Полную длину стрелочной улицы (проекцию) вычисляют по формуле: Lc =a+ L+ T= a+ ∑Е/tgα+T (21) где а – расстояние от центра стрелочного перевода до стыка рамных рельс, м; L – длина стрелочной улицы (проекция на горизонтальную ось) от центра перевода до вершины угла поворота крайнего пути, м; Т – тангенс кривой, м; Lc= 14,059+(5,3+5,3+5,3)/0,090909+13,608= 202,6 м. Построение стрелочной улицы под углом крестовины по данным см. в Приложении Б. 3.2.Простейшая стрелочная улица на основном пути Рассчитываем простейшую стрелочную улицу по основному пути парка отстоя локомотивов в резерве.  Рисунок 3.2 – Простейшая стрелочная улица по основному пути Решение: Расстояние между центрами стрелочных переводов вычисляют по формуле (16): l= Е/sinα l= 5,3/0,090563= 58,54 м Радиусы переводных кривых вычисляют по формулам: R2=R+Е R3=R+2Е (22) где R – радиус переводной кривой, соответствующего индекса, м; Е – ширина междупутья, м; R2=300+5,3=305,3 м R3=300+10,6=310,6 м Расстояние от начала или конца кривой до вершины угла поворота (Тангенс кривой) вычисляют по формуле (3): T1= R3tg  T2= R2tg  T3=Rtg  T1 = 310,6*0,045359=14,09 м T2= 305,3*0,045359=13,85 м T3=300*0,045359=13,608 м Длину вставки между концами стрелочного перевода и началом кривой вычисляют по формуле (5): ƒ1=(3Е/sinα)-(b+ T1) ƒ2= (2Е/sinα)-(b+ T2) ƒ3= (Е/sinα)-(b+ T3) ƒ1=(3*5,3/0,090536)-(20,795+ 14,09) =140,74 м ƒ2=(2*5,3/0,090536)-(20,795+ 13,85) = 82,44 м ƒ3=(5,3/0,090536)-(20,795+ 13,608) = 24,137 м Длину стрелочной улицы от центра перевода до вершины угла поворота крайнего пути вычисляют по формулам: L1-ВУ1=∑Е/tgα L2-ВУ2= (Е+Е)/sinα L3-ВУ3=Е/sinα L1-ВУ1= (5,3+5,3+5,3)/0,090909=174,9 м L2-ВУ2= (5,3+5,3)/0,090536=117,08 м L3-ВУ3= 5,3/0,090536=58,54 м Полную длину стрелочной улицы (проекцию) вычисляют по формуле: L=a+3*l+T3 (24) где а – расстояние от центра стрелочного перевода до стыка рамных рельс, м; l – расстояние между центрами стрелочных переводов, м; T3 – тангенс кривой; L=14,079+3*58,54+13,608=203,307 м. Построение стрелочной улицы на основном пути по данным см. в Приложении В. 4. Раздвижка путей На раздельных пунктах, расположенных на двухпутных участках железных дорог, производится уширение междупутья (Е) с 4,1 м до ширины междупутья на станции - 5,3 м. В этом случае применяется раздвижка путей (рис.1) с параллельным смещением одного из них (переход от междупутья перегона Е=4,1 м к междупутью станции Еуш=5,3 м). При раздвижке главных путей применяются радиусы кривых (R) 3000-4000м, а при скоростном движении (V =160 км/ч) – не менее 5000 м. Переходные кривые берутся по нормам и техническим условиям, а прямые вставки (d) между ними принимаются не менее 75 м ( и не менее 30 м в стесненных условиях). При раздвижке станционных путей станционных путей могут использоваться прямые вставки не менее 15м (см. учебник Скалов, приложение 2). Расчет раздвижки путей производится по формулам, приведенным ниже. 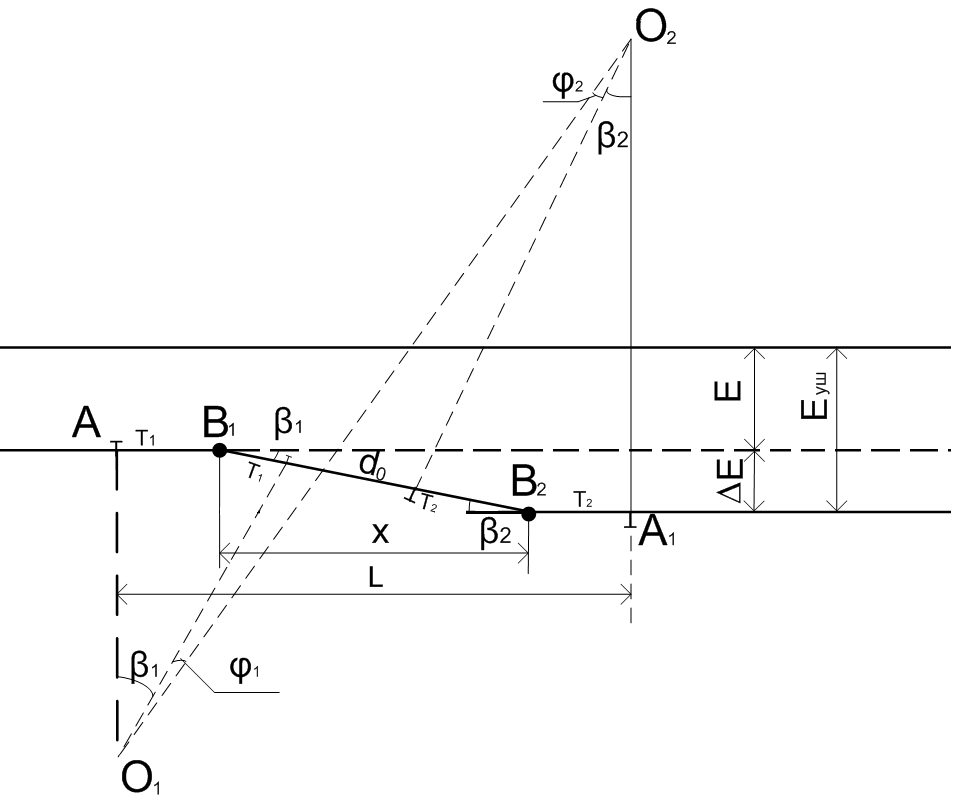 Рисунок 4 – Параллельное смещение (раздвижка) путей где Т – тангенс круговой кривой, т.е. расстояние от начала круговой кривой до вершины угла поворота ее; d0 – прямая вставка между обратными кривыми; L – общая длина (проекция) соединения между точками А и А1. Пример расчета: Дано: междупутье Е; радиус кривых R; прямая вставка d0. Определить: расписать словами β, Т, К, L. При скорости движения до 120км/ч при радиусе кривых R=4000 м, d0=75, Е=4,1м, Еуш= 5,3 м (см.рис.4) tgφ= 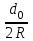 Уширение определяется:  ∆Е = Еуш – Е ∆Е = Еуш – Е |О1О2| 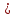 cos(β+φ) = 2R – ∆Е cos(β+φ) = 2R – ∆Е |О1О2| = 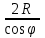   cos(β+φ) = 2R – ∆Е cos(β+φ) = 2R – ∆Е cos(β+φ) =   cos φ, приводим подобные: cos φ, приводим подобные:сos (β+φ) = (1– 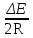 ) )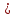 cos φ, подставим значения cos φ, подставим значенияcos (β+φ) = (1– 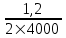 ) )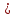 0,9999, получаем 0,9999, получаемcos (β+φ) = 0,99975 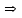 10, сумма углов 10, сумма угловβ+φ =10 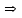 β =1– 0031’= 0029’ β =1– 0031’= 0029’К = R 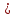 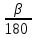 = 0,017453 = 0,017453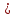 R R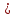 β0 β0T = R 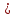 tg tg 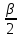 Общая длина (проекция) соединения между А и А1: L = 2T+(2T+ d0) 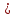 cosβ cosβtg φ= 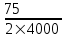 =0,009375 =0,009375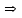 φ= 0031’ φ= 0031’К = 0,0017453*4000*0029’=20,245 м Т = 4000*tg 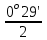 =16,5 м =16,5 мОбщая длина соединения между А и А1: L = 2T+(2T+ d0)  cosβ cosβL = 2*16,5+(2*16,5+75)*cos0029’=140,59 м X = L – 2T = 140.5 – 2*16,5 = 107,59 м. Построение раздвижки путей по данным см. в Приложении В. 5. Эпюра стрелочного перевода. Эпюра стрелочного перевода – схема взаимного расположения элементов стрелочного перевода с указанием их основных размеров. 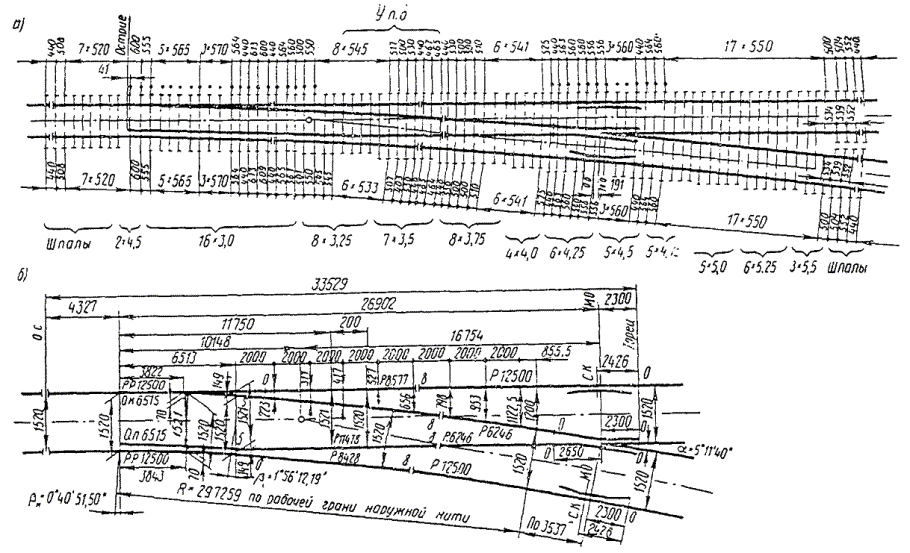 |
