Теория по теме: Анализ информационных моделей. Теория графов. 11 Класс. 1. Анализ информацонных моделей - теория. Использование и анализ информационных моделей (таблицы, диаграммы, графики)
 Скачать 3.97 Mb. Скачать 3.97 Mb.
|
|
© К. Поляков, 2009-2021 1 (базовый уровень, время – 3 мин)Тема: Использование и анализ информационных моделей (таблицы, диаграммы, графики). Что проверяется: Умение представлять и считывать данные в разных типах информационных моделей (схемы, карты, таблицы, графики и формулы). 1.3.1 Описание (информационная модель) реального объекта и процесса, соответствие описания объекту и целям описания. Схемы, таблицы, графики, формулы как описания 1.2.2. Умение интерпретировать результаты, получаемые в ходе моделирования реальных процессов. Что нужно знать: граф – это набор вершин и соединяющих их ребер; он описывается в виде таблицы (матрицы смежности или весовой матрицы) чаще всего используется взвешенный граф, где с каждым ребром связано некоторое число (вес), оно может обозначать, например, расстояние между городами или стоимость перевозки рассмотрим граф (рисунок слева), в котором 5 вершин (A, B, C, D и E); он описывается таблицей, расположенной в центре; в ней, например, число 4 на пересечении строки В и столбца С означает, что, во-первых, есть ребро, соединяющее В и С, и во-вторых, вес этого ребра равен 4; пустая клетка на пересечении строки А и столбца В означает, что ребра из А в В нет 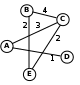 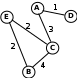
обратите внимание, что граф по заданной таблице (она еще называется весовой матрицей) может быть нарисован по-разному; например, той же таблице соответствует граф, показанный на рисунке справа от нее в приведенном примере матрица симметрична относительно главной диагонали; это может означать, например, что стоимости перевозки из В в С и обратно равны (это не всегда так) во многих задачах вес – это длина дороги из одного пункта в другой; для рассмотренного примера длина дороги из А в С равна 3, дороги из А в Е нет степень вершины – это количество рёбер, которые соединены с этой вершиной; при определении степени вершины по таблице нужно считать число непустых ячеек весовой матрицы в соответствующей строке (или столбце); в примере степень вершины А равна 2 (в первой строке две непустых ячейки со значениями 3 и 1) Пример задания:Р-10 (демо-2021). На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова протяжённость дороги из пункта Г в пункт Ж. В ответе запишите целое число – так, как оно указано в таблице. 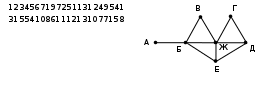 Решение: определим для каждой вершины её степень, то есть, количество ребёр, в которыми она связана; в таблице степень вершины – это количество заполненных клеток в строке (или в столбце) 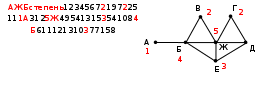 3 сопоставление степеней вершин в таблице и на рисунке позволяет сразу обнаружить в таблице вершины А (она имеет № 3), Ж (№ 4) и Б (№ 6) нас интересуют вершины Г и Ж; вершину Ж мы нашли, вершина Г имеет степень 2 и связана, кроме вершины Ж, с вершиной Д степени 3; степень 2 имеют вершины № 1 и 2, но только вершина № 1 связана, кроме Ж, с вершиной степени 3 (№ 7), поэтому вершина № 1 – это Г по таблице определяем протяжённость дороги из пункта Г в пункт Ж, она равна 9. Ответ: 9. |
