Теория по теме: Анализ информационных моделей. Теория графов. 11 Класс. 1. Анализ информацонных моделей - теория. Использование и анализ информационных моделей (таблицы, диаграммы, графики)

• Название: Использование и анализ информационных моделей (таблицы, диаграммы, графики)
• Анкор: Теория по теме: Анализ информационных моделей. Теория графов. 11 Класс
• Дата: 01.06.2022
• Размер: 3.97 Mb.
• Имя файла: 1. Анализ информацонных моделей - теория.doc
• Тип: Документы; #563649
• страница: 3 из 16

Ещё пример задания:

Р-08. На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Е. В ответе запишите целое число – так, как оно указано в таблице.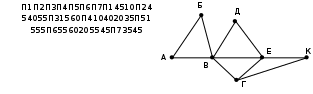



Решение:

1. 
   для того чтобы определить нужные нам вершины В и Е в весовой матрице, легче всего подсчитать степени вершин, то есть для каждой вершины найти количество рёбер, с которыми она связана (петля – ребро, которое соединяет вершину саму с собой, как кольцевая дорога, считается дважды)
   
2. 
   в весовой матрице степень вершины – это количество непустых клеток в соответствующей строке (показаны справа от таблицы на жёлтом фоне), а для изображения графа- количество пересечений небольшой окружности, проведённой около вершины, со всеми рёбрами: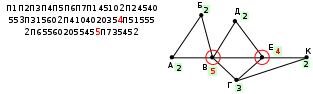
   

3. 
   по изображению графа находим, что вершина В имеет степень 5, а вершина Е – степень 4
   
4. 
   в таблице есть ровно одна вершина, степень которой 5 (это П6) и одна вершина, степень которой – 4 (П4), их соединяет ребро длиной 20 (эти ячейки выделены в весовой матрице фиолетовым фоном).
   
5. 
   Ответ: 20.
   
6. 
   Бонус: попытаемся теперь определить, как обозначены остальные вершины в таблице. Каждая из вершин Д (степени 2) и Г (степени 3) соединена с уже известными вершинами В и Е, по таблице находим, что вершина Д – это П7, а вершина Г – это П2. Тогда вершина К соединяется с Е (П4) и Г (П2), то есть К – это П1. А вот различить вершины А и Б по этим данным не удаётся.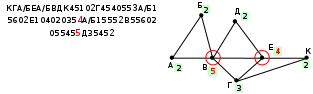
   

Ещё пример задания:

Р-07. На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта А в пункт Д. В ответе запишите целое число – так, как оно указано в таблице.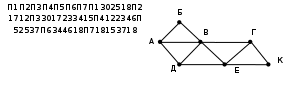



Решение:

1. 
   определим степени вершин по весовой матрице и по изображению графа (как в предыдущей задаче):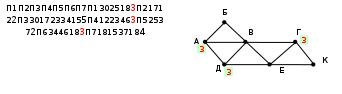
   

2. 
   по изображению графа находим, что обе интересующих нас вершины, А и Д, имеют степени 3; кроме того, степень 3 имеет еще и вершина Г
   
3. 
   в таблице тоже есть три вершины со степенью 3 (это П1, П4 и П6), но вершина П1 (это вершина Г на рисунке!) не имеет общих ребёр с вершинами П4 и П6 (а это А и Д!);
   
4. 
   таким образом, ответ – это длина ребра между вершинами П4 и П6 (эти ячейки выделены в весовой матрице фиолетовым фоном).
   
5. 
   Ответ: 46.
   
6. 
   Бонус: вершины В и Е, имеющие степени 5 и 4, это П3 и П7; с вершиной Г (П1) связана ещё вершина К, имеющая степень 2 – это П5; с Е связана ещё вершина Д – это П6; тогда П4 – это А, а П2 – это Б.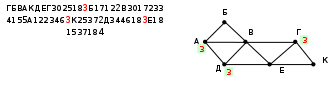
   

Ещё пример задания:

Р-06. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)

	A	B	C	D	E	F
A		2	4	8		16
B	2			3
C	4			3
D	8	3	3		5	3
E				5		5
F	16			3	5

Определите длину кратчайшего пути между пунктами A и F, проходящего через пункт E и не проходящего через пункт B. Передвигаться можно только по указанным дорогам.

Решение:

1. 
   поскольку нас интересуют только маршруты, НЕ проходящие через пункт В, столбец и строку, соответствующие этому пункту, можно удалить из таблицы:
   

   	A	C	D	E	F
   A		4	8		16
   C	4		3
   D	8	3		5	3
   E			5		5
   F	16		3	5

2. 
   дальше действуем так же, как показано при решении следующих далее разобранных задач; причем из всех маршрутов нужно оставить только те, которые проходят через пункт Е
   
3. 
   первый шаг от А (в скобках указаны длины маршрутов):
   

АС (4), AD (8)

прямой маршрут AF не рассматриваем, потому что он не проходит через пункт E

4. 
   второй шаг
   

ACD (7), ADC (11), ADE (13)

маршрут ADF не рассматриваем, потому что он не проходит через пункт E

5. 
   третий шаг:
   

ACDE (12), ADEF (18)

маршрут ADEF дошел до пункта назначения;

маршрут ADC продолжать не имеет смысла, потому что из C можно проехать только в пункты A и D, где мы уже были;

маршрут ACDF не рассматриваем, потому что он не проходит через пункт E

6. 
   четвертый шаг:
   

ACDEF(17)

7. 
   этот маршрут тоже дошел до пункта назначения, его длина меньше, чем для предыдущего, его и выбираем
   
8. 
   Ответ: 17.