курсовая работа. алгебра. Использование кейстехнологии при обучении алгебре в основной школе
 Скачать 0.93 Mb.
|
|
2.1 Учебно-тематическое планирование использования «кейс-метода» на уроках алгебры в 8 классе С целью активизации учебно-познавательной деятельности обучающихся на уроках алгебры в 8 классе нами был разработан цикл уроков с использованием «кейс-метода» (таблица 3). Таблица №3 Учебно-тематическое планирование использования «кейс-метода» на уроках алгебры в 8 классе
2.2. Конспекты уроков алгебры для 8 класса Конспект 1. Урок алгебры в 8 классе  Тема урока: Решение задач с помощью квадратных уравненийЦель урока: создать условия для активизации учебно-познавательной деятельности обучающихся и формирования опыта применения  полученных знаний по теме «Квадратные уравнения» в конкретных жизненных ситуациях [4].Основные этапы урока: 1.Мотивация к учебной деятельности (5 мин.) 2. Актуализация знаний (10 мин.) 4.Работа с кейсом (20 мин.) 5.Постановка домашнего задания (2 мин.) 6.Итог урока, рефлексия (3 мин.) Ход урока . Мотивация учебной деятельности Приветствие обучающихся. Цель урока - получить опыта применения полученных знаний по теме «Квадратные уравнения» в конкретных жизненных ситуациях. (Приветствуют учителя, показывают готовность к уроку. Делают пометки исторической справки) 10. Актуализация знаний - Ребята, сегодня у нас необычный урок. У каждого на столе лежат оценочные листы, туда вы будете отмечать набранные вами баллы, и в конце урока, суммировав эти баллы, получите оценку. Прежде чем мы начнем работать по теме урока, ответьте на блиц опрос. Блиц – опрос (вставить пропущенные слова) -Уравнение вида ах2 bx c 0, где a, b, c - заданные числа, a0, x -переменная, называется? (квадратным уравнением) [20] -По дискриминанту можно определить количество корней квадратного уравнения. Какой количество корней будет, если дискриминант больше нуля? (два корня) - Если дискриминант равен нулю? (один корень) - Если дискриминант меньше нуля? (корней нет)  - Уравнения вида a0, c0 и ах2 bx 0, где а0 и в0 называют? (неполным квадратным уравнением)-Составить квадратное уравнение, если, а=-4, в=1, с=-12 (4х2 x 12 0) -Дано уравнение3x2 7x 4 0 . Чему равен дискриминант? (1) «Кейс»: «2 водителя» Описание ситуации «Как помочь Сергею?» «Две дороги пересекаются под прямым углом. От перекрестка одновременно отъехали два велосипедиста, Сергей поехал в южном направлении, а Дмитрий – в восточном. Скорость Дмитрия была на 4 км/час больше скорости Сергея. Сергей утверждал, что через час расстояние между ними оказалось равным 20 км, а Дмитрий не поверил расчётам друга. Как помочь Сергею убедить друга?» ПРАВИЛА РАБОТЫ С КЕЙСОМ 1. Двукратное чтение кейса: один раз, чтобы иметь общее представление и второй раз, чтобы хорошо разобраться в фактах. 2. Составить список проблем, с которыми придется иметь дело. 3. Если предлагаются цифровые данные, нужно попытаться их оценить и объяснить. 4. Выявить проблему, к которой можно применить имеющиеся знания. 5. Составить основательный анализ имеющейся ситуации. 6. Поддержка предложений решения проблемы посредством основательной аргументации. - Вы разбиты на группы. У каждой группы на столе лежит «кейс» с заданием. Необходимо составить схему, таблицу, рисунок, которые дают основание для «решения» и решить кейс. Прежде чем приступить к решению кейса, запишите в тетрадь алгоритм решения текстовой задачи: 1)Выбрать величину и обозначить буквой 2) Составить уравнение, исходя из условия задачи 3) Решить уравнение 4) Соотнести найденные значения корней с условием задачи 5)Записать ответ, соответствующий вопросу задачи [17] Текстовая задача на движение. Чтобы выполнить это задание, ученик должен составить и решить уравнение по условию, правильно интерпретировать полученный результат. - В какой форме лучше записать условие задачи: рисунок, таблица, краткая запись или что-то другое? (с помощью прямого треугольника) - Как связаны между собой скорость, время и пройденный путь? (S=V*T расстояние равно скорость умноженное на время) - Вспомните теорему Пифагора для составления уравнения (квадрат гипотенузы равен сумме квадратов катетов) - Что принять за неизвестную величину – Х? (Скорость Сергея, т.е. наименьший катет) Обучающиеся решают задачу. Решение: Начертим рисунок. Изобразим прямоугольный треугольник (см. рисунок 6). 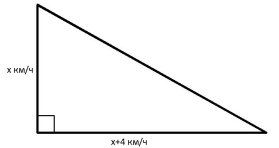 Риcунок 1 Для решения задачи применим теорему Пифагора. Итак, скорость первого велосипедиста обозначим х км/ч, скорость второго (х+4) км/ч. Первый за 1 час проехал расстояние х км/ч * 1 ч =х км, а второй (х+4)км/ч * 1 ч =х+4 км Расстояние между велосипедистами (это гипотенуза прямоугольного треугольника) через 1 час оказалось 20 км. Составим уравнение для решения задачи: x=12(км/ч)-скорость первого х+4=12+4=16(км/ч)- скорость второго - Мы приближаемся к концу урока, попрошу вас ответить на вопросы по исторической справке и ответьте на вопросы (индивидуально) - В каком веке жил Декарт? (в 17 веке) - Какие науки его интересовали? (философия, алгебра, биология и физика) - Назовите самую известную работу? (изобретение координатных прямой и плоскостей.) - Какие открытия сделал Рене Декарт? (В физиологии он ввел понятие рефлекса, закон преломления света, поясняющий образование радуги) -Что удивило вас в этом человеке? (Каждый дает свой ответ) - Крылатое высказывание Декарта? (Мало иметь хороший ум, главное хорошо его применять») Оцените себя, запишите набранный вами балл в оценочный лист. Рефлексия Заполни анкету: Постановка домашнего задания Подготовка к контрольной работе [3]. Конспект 2. Урок алгебры в 8 классе Тема: «Решение уравнений» Цель урока: показать обучающимся различные способы решения одной и той же задачи, способствовать формированию у обучающихся нахождения своего пути решения задачи, предоставить обучающемуся возможность правильно ориентироваться в ситуации выбора  Основные этапы урока:1.Мотивация к учебной деятельности (5 мин.) 2. Актуализация знаний (10 мин.) 3.Работа с кейсом (20 мин.) 4.Постановка домашнего задания (2 мин.) 5.Итог урока, рефлексия (3 мин.) Ход урока 1. Мотивация к учебной деятельности. Приветствие обучающихся. Цель урока - научиться решать уравнения различными способами. «Уравнение – это золотой ключ, открывающий все математические сезамы» С. Коваль; 1.разложение на множители способом группировки 2. выделение полного квадрата 3.сведение уравнения к квадратам в левой и правой части. 4. графический метод 5. Актуализация знаний. Разминка: (игра – запомни квадрат, упражнение на развитие зрительной памяти)  Открыть квадрат, находящийся на доске слева. 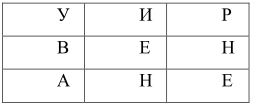 За 15 секунд обучающимся предлагается запомнить буквы и их расположение в клетках квадрата, затем квадрат убирается, а ученики должны восстановить в тетради такой же квадрат. Устный опрос:  Обучающимся предлагается расшифровать имя учёного, о котором шла речь в исторической справке. 1. Какое уравнение решается излечением квадратного корня? ( Д) 2. Какое уравнение решается вынесением общего множителя за скобки? (И ) 3. Какое уравнение можно решить, применив формулу квадрата суммы двух выражений? (О) 4. Какое уравнение решается, используя формулу разности квадратов? (Ф) 5. Какое уравнение не имеет решений (А) 6. Какое уравнение можно упростить, разделив обе части на 3? (Н) 7. Какое уравнение имеет корень = 0? (Т) Работа с кейсом. -Наш урок сегодня будет посвящён одному уравнению. Мы с вами ещё не знакомы с общими формулами решения квадратных уравнений, поэтому попробуем решить уравнение 3х2 + 2х – 1 = 0, применяя уже изученные нами методы решения. ПРАВИЛА РАБОТЫ С КЕЙСОМ 1. Двукратное чтение кейса: один раз, чтобы иметь общее представление и второй раз, чтобы хорошо разобраться в фактах. 2. Составить список проблем, с которыми придется иметь дело. 3. Если предлагаются цифровые данные, нужно попытаться их оценить и объяснить. 4. Выявить проблему, к которой можно применить имеющиеся знания. 5. Составить основательный анализ имеющейся ситуации. 6. Поддержка предложений решения проблемы посредством основательной аргументации. 7. Составить схему, таблицу, рисунок, которые дают основание для «решения». - Вы разбиты на 4 группы. У каждой команды на столе лежит «кейс»-задание. Группа решает свое задание и выбирает командира, в конце урока командир каждой команды готовит выступление, где будет показывать свой метод решения уравнения. Остальные ребята фиксируют каждый метод решения у себя в тетрадях [8]. ЗАДАНИЯ 1 ГРУППЕ: ознакомиться с литературой по данному методу, решить уравнение разложением на множители способом группировки. Проанализировать свою работу, выделить трудности решения данным способом и плюсы. ЗАДАНИЯ 2 ГРУППЕ: ознакомиться с литературой по данному методу, решить уравнение методом выделения полного квадрата. Проанализировать свою работу, выделить трудности решения данным способом и плюсы. ЗАДАНИЯ 3 ГРУППЕ: ознакомиться с литературой по данному методу, решить уравнение Метод сведения уравнения к квадратам левой и правой части. Проанализировать свою работу, выделить трудности решения данным способом и плюсы. ЗАДАНИЯ 4 ГРУППЕ: ознакомиться с литературой по данному методу, решить уравнение графическим методом Проанализировать свою работу, выделить трудности решения данным способом и плюсы. Первый способ: Разложение на множители способом группировки. 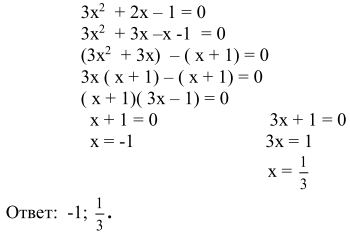 Второй способ: Метод выделения полного квадрата. 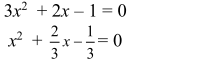 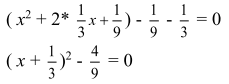 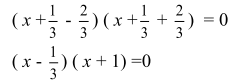 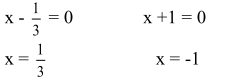  Третий способ: Метод сведения уравнения к квадратам левой и правой части. 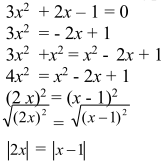 Для решения уравнения, содержащего модуль, рассмотрим следующие случаи: 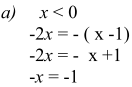   Четвертый метод: Графический способ 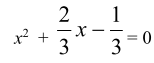 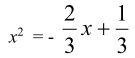  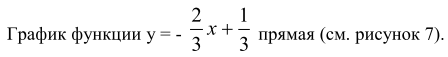  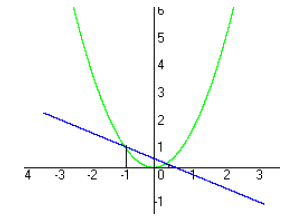  Рисунок 2  1 Ответ: -1; 3 . 4. Рефлексия. Подведение итогов урока: Анализ результатов. Определение наилучшего способа решения квадратного уравнения каждому ученику. Оценка работы групп, оценка выступление возле доски командиров. 5. Домашнее задание: Решить различными способами уравнение 2х2 - 9х + 10 = 0. Конспект 3. Урок алгебры в 8 классе  Тема урока: Решение квадратных уравненийЦель урока: создать условия для активизации учебно-познавательной деятельности обучающихся и формирования опыта применения полученных знаний по теме «Квадратные уравнения» в конкретных жизненных ситуациях. Основные этапы урока [14]: 1.Мотивация к учебной деятельность (5 мин.) 2.Актуализация знаний(5 мин.) 3.Работа с кейсом(30 мин.) 4.Постановка домашнего задания(2 мин.) 5.Рефлексия (3 мин.) Ход урока 1. Мотивация к учебной деятельности -Здравствуйте, ребята! Алгебру не зря называют «царицей наук», ей больше, чем какой-либо другой науке, свойственны: красота, изящность и точность. Одно из замечательных качеств алгебра - любознательность. Постараемся доказать это на уроке. Вы начали изучать новый большой раздел «Квадратные уравнения». Знания не только надо иметь, но и надо уметь их показать, что вы и сделаете на сегодняшнем уроке, а я вам в этом помогу. (Приветствуют учителя, показывают готовность к уроку). -Ребята, скажите, кто-нибудь из вас слышал о таком понятии как компетентность? Компетентность – это вид деятельности, который освоен очень хорошо. Вот и мы с вами для того, чтобы достигнуть поставленную цель должны овладеть следующими компетентностями: 1.Определю вид квадратного уравнения, коэффициенты уравнения. 2.Решаю три вида неполных квадратных уравнений. 3.Решаю квадратные уравнения по формуле. - Сейчас предлагаю вам определить какими вы хотите обладать компетентностями к концу нашего урока и наклеить около нее яблочко ожиданий с вашим именем. А в конце урока мы вернемся к нашим яблочкам. 2. Актуализация знаний На доске карточки ах2 + вх + с = 0, ах2 + 2кх + с = 0, х2 + рх +q = 0, Под ними хаотично расположены следующие карточки: Д = в2 – 4ас, х1 + х2 = – р, Д1 = к2 – ас, х1 • х2 = q, - Какие уравнения называют квадратными? ( Квадратным уравнением называют уравнение вида ах2 + вх + с = о, где коэффициенты а, в, с – любые действительные числа, причем, а =/= 0) -Как называют каждое из уравнений на карточках? |