Использование математической статистики в анализе авторства текста. Отчет -ПетровА.М.-Дворянов Н.А.-681-12. Использование математической статистики в анализе авторства текста по дисциплине Статистические методы анализа данных
 Скачать 0.6 Mb.
|
ВОЕННО-КОСМИЧЕСКАЯ АКАДЕМИЯ ИМЕНИ А.Ф. МОЖАЙСКОГОКафедра систем сбора и обработки информации Факультет специальных информационных технологий Курсовая работаТема: «Использование математической статистики в анализе авторства текста» по дисциплине «Статистические методы анализа данных» Выполнили: курсанты 681/12 учебной группы:рядовой Петров А.М. рядовой Дворянов Н.А. Проверил: Санкт-Петербург 2020 г.СОДЕРЖАНИЕВОЕННО-КОСМИЧЕСКАЯ АКАДЕМИЯ ИМЕНИ А.Ф. МОЖАЙСКОГО 1 ВВЕДЕНИЕ 4 ИСПОЛЬЗУЕМЫЕ МЕТОДЫ СТАТИСТИЧЕСКОГО АНАЛИЗА В РАБОТЕ 5 ХОД РАБОТЫ 6 АЛГОРИТМ РАБОТЫ ПРОГРАММЫ И ОПРЕДЕЛЕНИЯ АВТОРОВ ТЕКСТОВ 16 ВЫВОД 17 ВВЕДЕНИЕВ современном мире все активнее ставится проблема установления авторства текстов. С развитием интернета многократно увеличился рост использования различного рода научных, исследовательских работ, дипломов и диссертаций, литературных произведений людьми, авторами которых они не являлись. Нельзя не отметить актуальность определения авторства текстов и в криминалистике, ведь, зачастую, от этого может зависеть решение суда. Также данная тема важна и для историков, литературоведов, исследующих произведения, автор которых до сих пор не был установлен. В своей работе мы попытаемся определить возможность установления автора текста с помощью математической статистики. Целью данной работы является разработка программного средства для возможности распознавания авторства текста на основе биграмм (сочетаний двух букв русского языка без пробелов и служебных символов) и анализ результатов ее работы с использованием математической статистики. Для достижения нашей цели будет создана программа на языке python, разбивающая любые тексты на биграммы и переносящая результаты в excel, где, с помощью математической статистики производится вычисление критерия корреляции Пирсона, дисперсионного анализа. 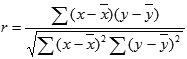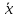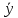ИСПОЛЬЗУЕМЫЕ МЕТОДЫ СТАТИСТИЧЕСКОГО АНАЛИЗА В РАБОТЕКритерий корреляции Пирсона В  своей работе мы использовали корреляцию Пирсона (Функция ПИРСОН в excel), где x – выборка, состоящая из частоты появления биграмм в тексте известного автора y - выборка, состоящая из частоты появления биграмм в исследуемом тексте  – среднее значение частоты появления биграмм в тексте известного автора – среднее значение частоты появления биграмм в исследуемом текстеДанную функцию используют в работе в том случае, когда необходимо отразить степень линейной зависимости между двумя массивами данных. Величина коэффициента линейной корреляции Пирсона не может превышать +1 и быть меньше чем -1. Эти два числа +1 и -1 – являются границами для коэффициента корреляции. Когда при расчете получается величина большая +1 или меньшая -1 – следовательно, произошла ошибка в вычислениях. Если коэффициент корреляции по модулю оказывается близким к 1, то это соответствует высокому уровню связи между переменными. Выбор корреляции Пирсона для определения автора исследуемого текста обусловлен тем, что независимо от вида выборки мы можем определить уровень связи между двумя выборками. ХОД РАБОТЫПолучение исходных данных Для данной курсовой работы мы выбрали по два текста у пяти разных авторов и ввели их вместе в разные текстовые документы: Александр Блок (Двенадцать; Незнакомка) – Блок.txt Максим Горький (Челкаш; Макар Чудра) – Горький.txt Сергей Есенин (Анна Снегина; Черный человек) – Есенин.txt Василий Жуковский (Сказка о царе Берендее; Спящая царевна) – Жуковский.txt Николай Некрасов (Крестьянские дети; Русские женщины) – Некрасов.txt Далее мы разработали программу, которая выполняет следующие функции: Разбивает любой текст на биграммы (наборы из двух символов русского алфавита без пробелов и служебных знаков), Выводит статистику появления биграмм в загруженном тексте в excel-файл Строит график количества биграмм в загруженном тексте (Только при запуске через редактор исходного кода, например, Visual studio code)  Рисунок 1. Фрагмент кода программы на языке Python Представление выборки Выборка представляет собой количество биграмм в загруженном тексте, отсортированных по алфавиту (начиная с «аа», заканчивая «яя»). Количество биграмм в русском алфавите равняется 33*33 = 1089 возможных вариаций. 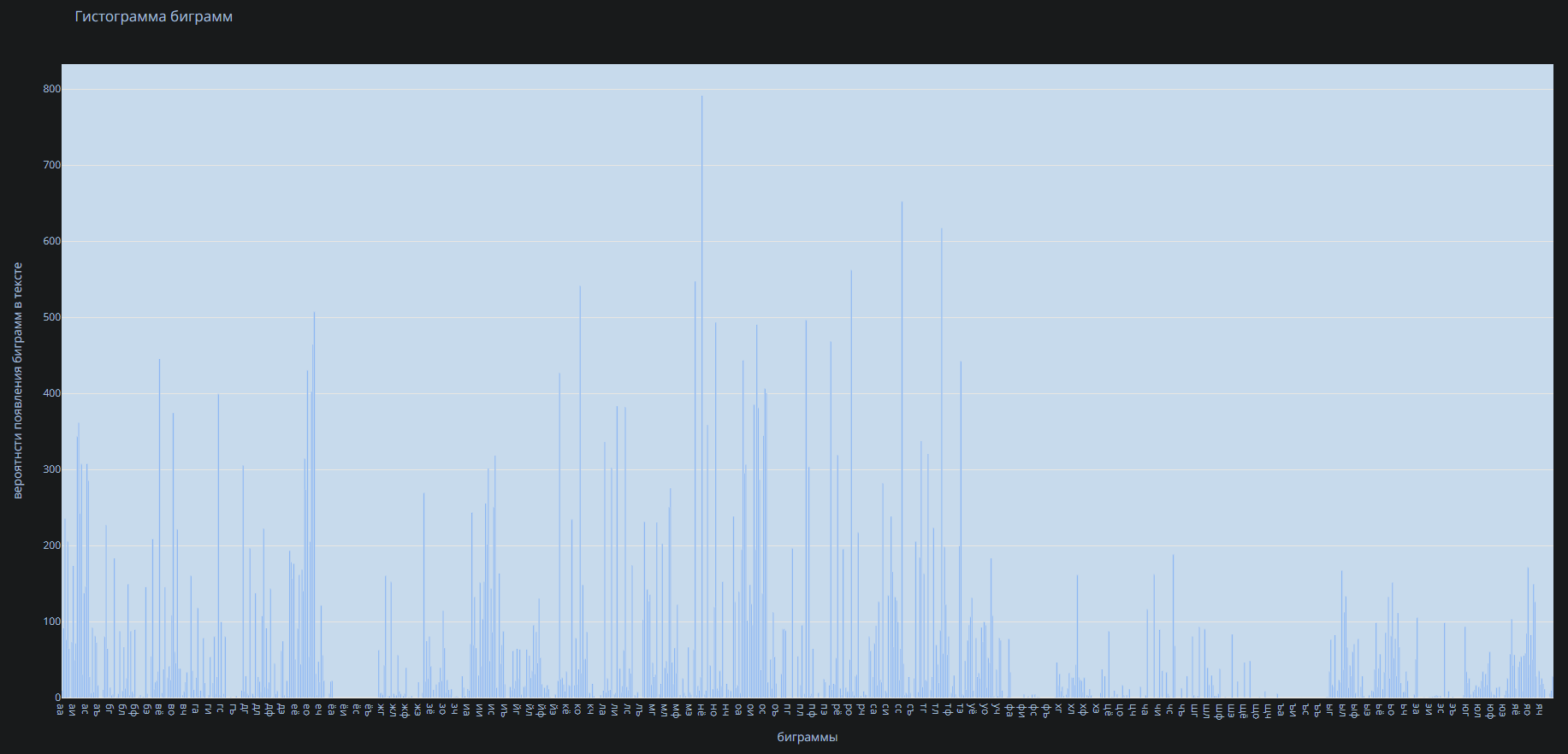 Рисунок 2. Пример гистограммы биграмм в загруженном тексте 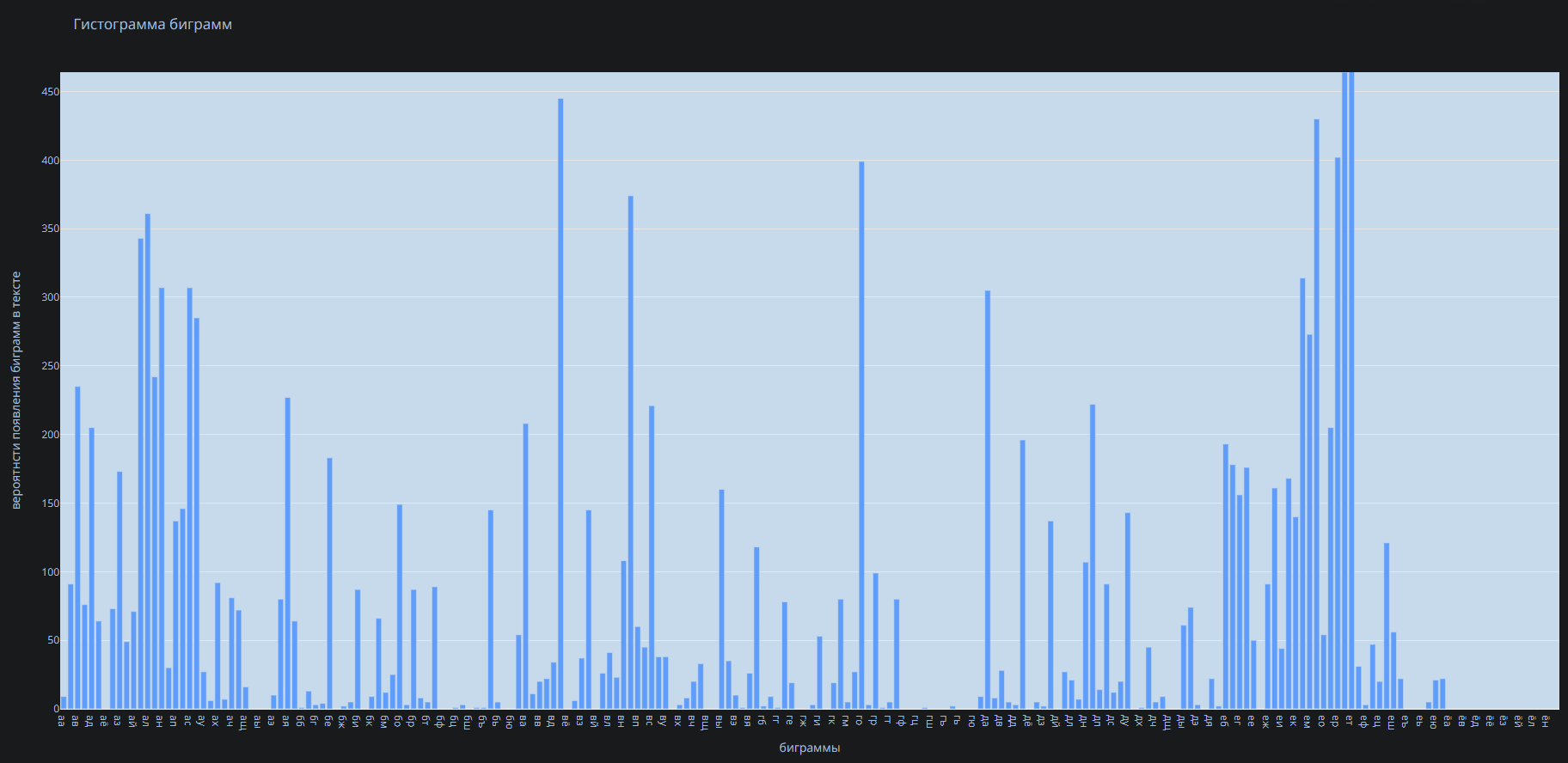 Рисунок 3. Пример гистограммы биграмм в загруженном текста в более крупном масштабе Статистический анализ выборки С помощью нашей программы, мы вычислили частоту появления биграмм для каждого автора и внесли все данные в таблицы excel. Названия листов в excel – это фамилии авторов Ячейка А1 – Названия выбранных текстов у данного автора Столбец F – Все существующие биграммы Столбец G – Количество биграмм в загруженном тексте Ячейка H1 – Сумма количества всех биграмм в загруженном тексте Столбец I – Частота появления биграмм в загруженном тексте Столбец O – Краткое описание столбцов 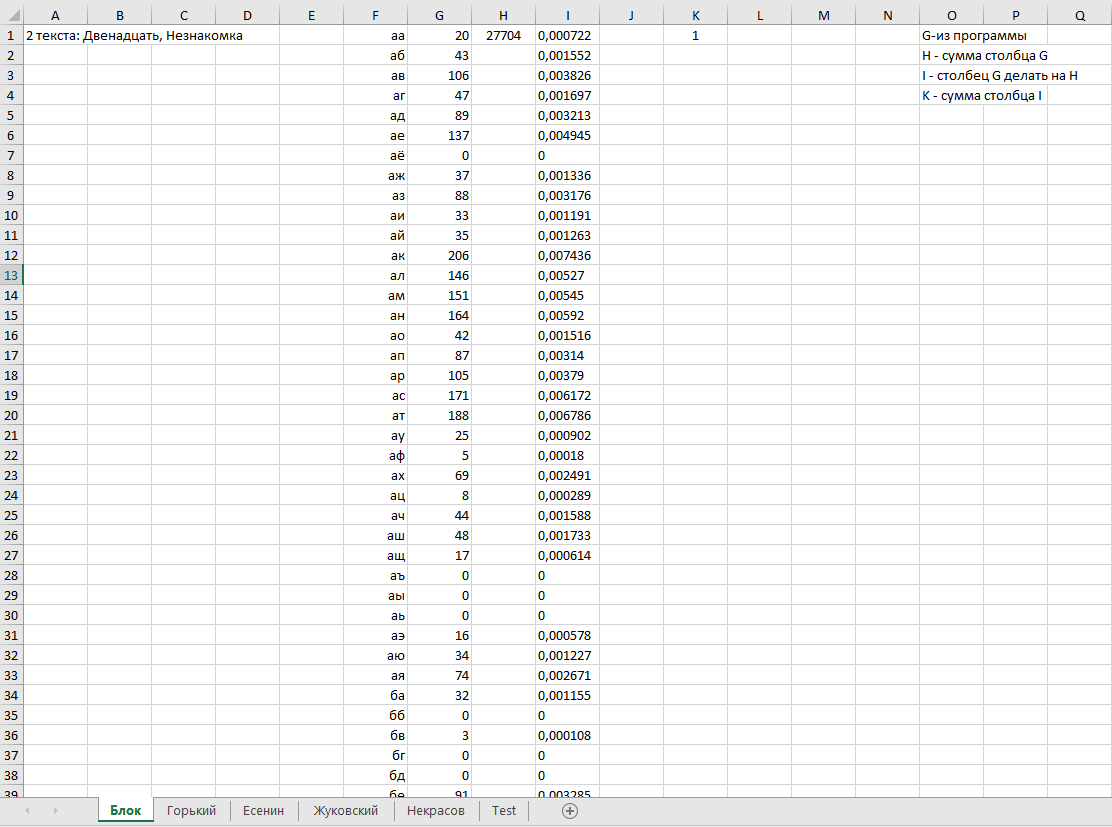 Рисунок 4. Статистика биграмм в произведениях Александра Блока 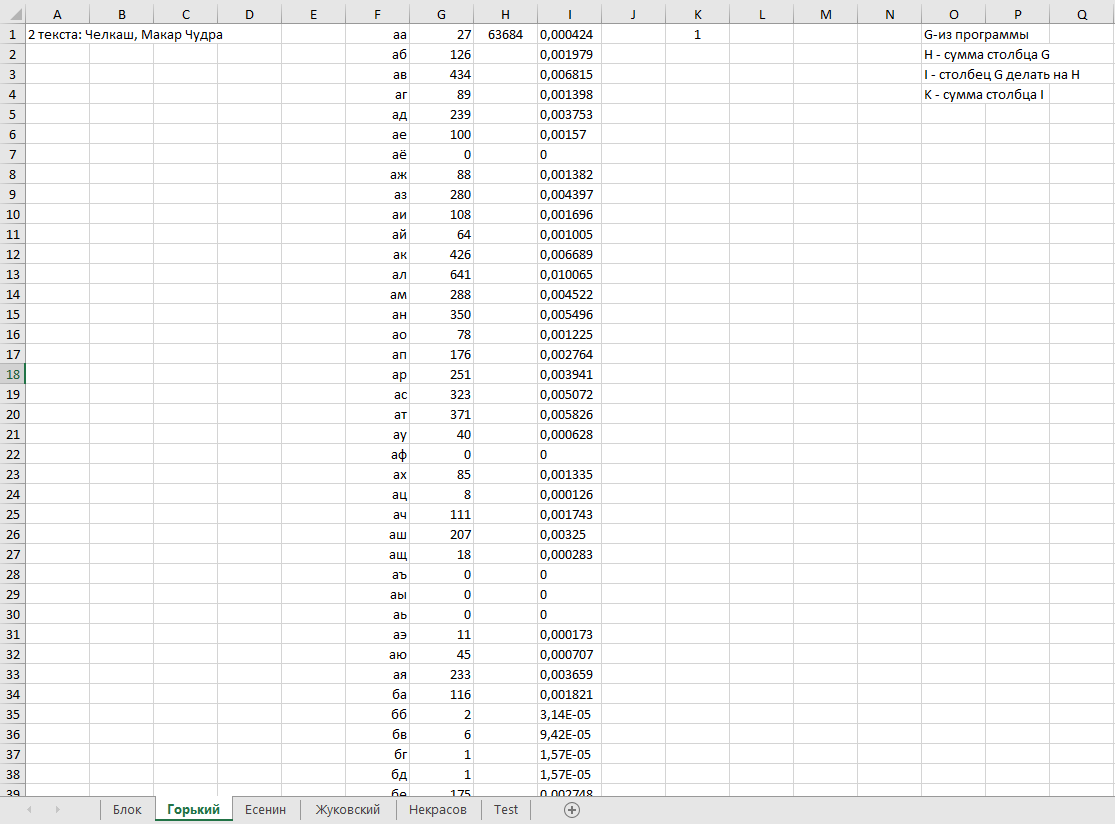 Рисунок 5. Статистика биграмм в произведениях Максима Горького 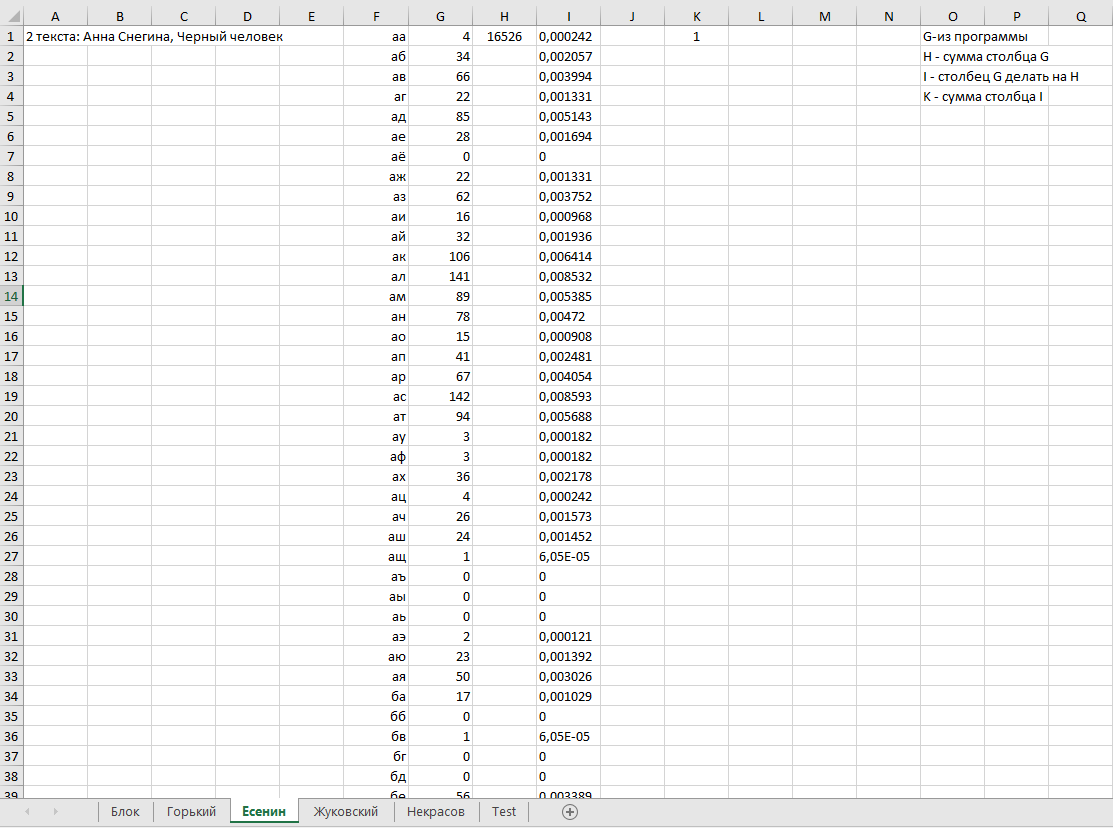 Рисунок 6. Статистика биграмм в произведениях Сергея Есенина 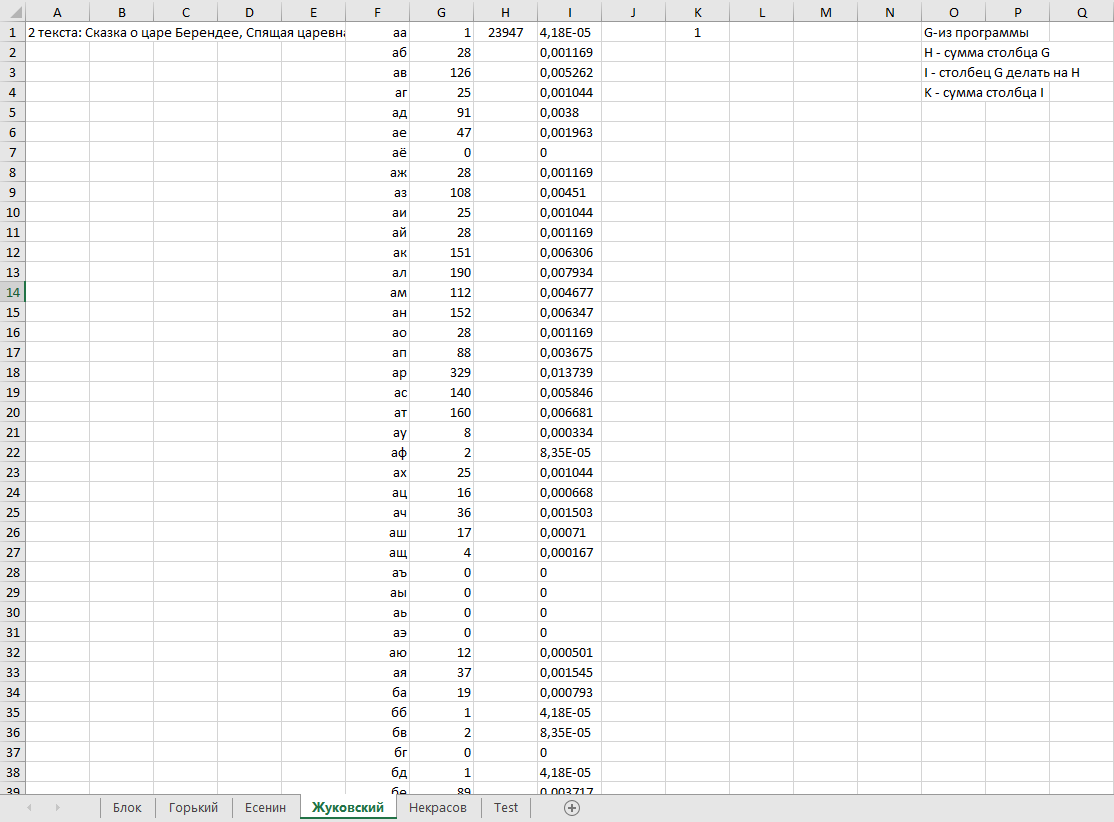 Рисунок 7. Статистика биграмм в произведениях Василия Жуковского 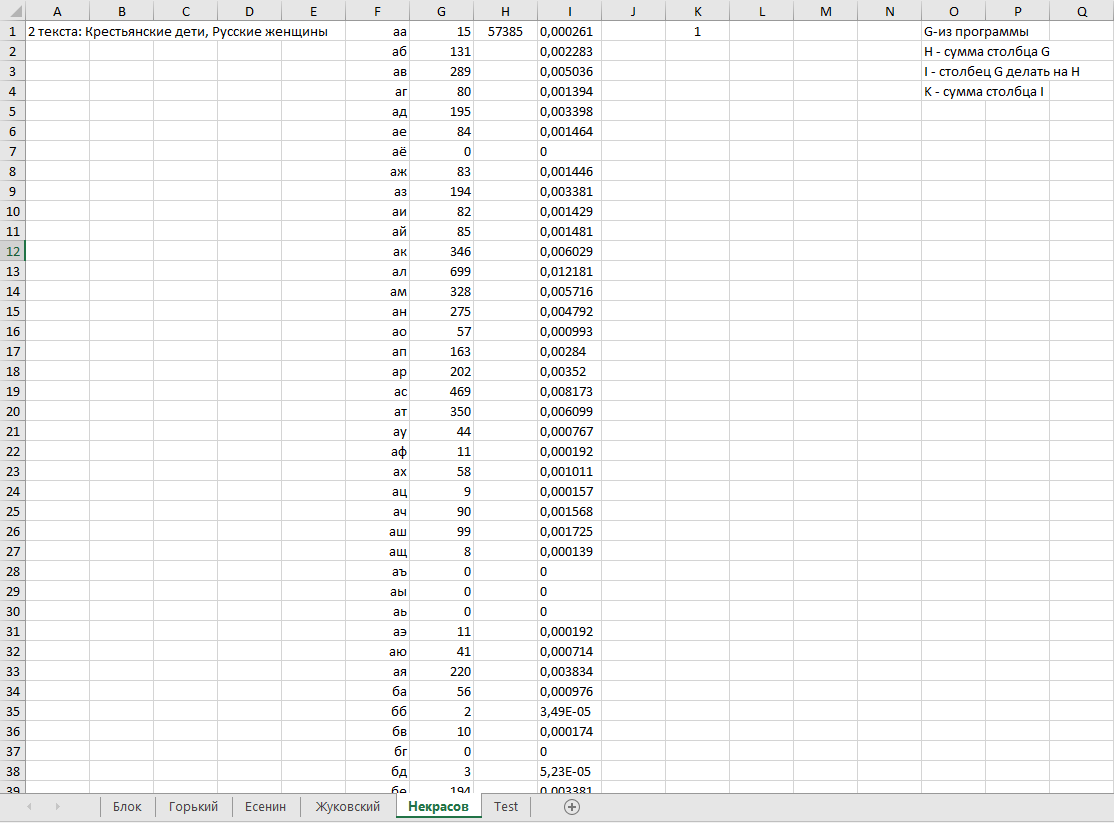 Рисунок 8. Статистика биграмм в произведениях Николая Некрасова После получения данных по исследуемым авторам, мы можем загружать любой из десяти текстов выбранных авторов для вычисления степени связи исследуемой выборки текста и исходных выборок по авторам, используем статистический критерий Пирсона в excel. Пример №1: Возьмем один из двух текстов Максима Горького - «Челкаш». Загрузим его в файл text_for_analysis.txt Запускаем программу Analyzer.exe Открываем наш excel файл, открываем лист «Test» и смотрим статистику. Таблица №1. Полученная статистика при загрузке текста М. Горького «Челкаш»
По данной таблице видно, что наивысший коэффициент корреляции Пирсона (связь) составляет 0,996266, что соответствует автору М. Горький. Пример №2: Возьмем один из двух текстов Александра Блока - «Незнакомка». Загрузим его в файл text_for_analysis.txt Запускаем программу Analyzer.exe Открываем наш excel файл, открываем лист «Test» и смотрим статистику. Таблица №2. Полученная статистика при загрузке текста А. Блока «Незнакомка»
По данной таблице видно, что наивысший коэффициент корреляции Пирсона (связь) составляет 0,99594, что соответствует автору А.Блок. Проверим поочередно каждый из десяти текстов авторов и составим таблицу результатов. Таблица №3. Результаты проверки одного из двух текстов для каждого из авторов
Как видно из таблицы, статистика точно определила авторов текстов. Теперь проверим тексты, которые не входили в исходный файл с двумя текстами, по которым составлялась статистика биграмм для каждого автора. Таблица №4. Результаты проверки текстов, не входящих в изначальную статистику для каждого из авторов
Из таблицы видно, что при вводе десяти других текстов выбранных авторов, только 70% из них определились верно. Попробуем это исправить. Составим новый текстовый документ, содержащий в себе четыре текста автора В. Жуковского: «Сказка о царе Берендее», «Спящая царевна», «Людмила», «Двенадцать спящих дев». Получим новую частоту появления биграмм для автора В. Жуковского, заменим старую статистику биграмм автора на новую. Пример №3. Возьмем текст В. Жуковского - «Людмила». Загрузим его в файл text_for_analysis.txt Запускаем программу Analyzer.exe Открываем наш excel файл, открываем лист «Test» и смотрим статистику. Таблица №5. Полученная статистика при загрузке текста В. Жуковского «Людмила»
По данной таблице видно, что наивысший коэффициент корреляции Пирсона (связь) составляет 0,934475, что соответствует автору В. Жуковский. Пример №4. Возьмем текст В. Жуковского - «Двенадцать спящих дев». Загрузим его в файл text_for_analysis.txt Запускаем программу Analyzer.exe Открываем наш excel файл и смотрим статистику Таблица №6. Полученная статистика при загрузке текста В. Жуковского «Двенадцать спящих дев»
По данной таблице видно, что наивысший коэффициент корреляции Пирсона (связь) составляет 0,983960658, что соответствует автору В. Жуковский. АЛГОРИТМ РАБОТЫ ПРОГРАММЫ И ОПРЕДЕЛЕНИЯ АВТОРОВ ТЕКСТОВДля определения автора текста нужно: Если открыт файл Data.xlsx, закрыть его! Открыть файл text_for_analysis.txt и ввести в него любой текст, сохранить файл Запустить программу Analyzer.exe и дождаться закрытия консольного окна Открыть файл Data.xlsx Открыть лист «Test» Посмотреть нужную статистику: Статистика по авторам находится в ячейках S1 – T5. Итоговый результат (наибольший коэффициент корреляции Пирсона) и соответствующий ему автор находятся в ячейках O10 – R11. Описание работы программы и файла excel: При открытии файла Analyzer.exe, происходит удаление всех лишних символов из файла text_for_analysis.txt, разбиение его на биграммы и подсчет биграмм. Все данные по биграммам выводятся в файл Data.xlsx, лист «Test», колонку G. С помощью формул происходит автоматический подсчет коэффициента корреляции Пирсона для каждого автора и загруженного текста. В отдельные ячейки выводится наибольший коэффициент корреляции Пирсона и соответствующий ему автор. ВЫВОДПосле проведенного исследования можно сделать вывод о том, что с помощью статистических методов можно с высокой вероятностью определить автора текста. Если вычислить количество биграмм для небольшого количества произведений автора вместе, то с большой вероятностью статистика количества биграмм отдельно взятого произведения правильно определит автора этого произведения. Если вычислить статистику по большому количеству произведений автора, то с большой вероятностью, ранее не добавленные в статистику произведения этого автора верно определят свою принадлежность к нему. При возникновении ошибок, можно добавлять в статистику ранее не исследованные произведения данного автора. Благодаря этому исправляются ошибки текста, который ранее определял автора неправильно, а также уменьшается вероятность появления ошибок в других, ранее не исследованных произведениях данного автора. Для определения авторства текста с высокой вероятностью, необходимо собрать в одном файле как можно больше текстов данного автора и провести подсчет биграмм в этом файле. После этого, используя коэффициент корреляции Пирсона, можно определить принадлежность текста к данному автору. |