ЦОС лабораторная работа. Исследование быстрого преобразования Фурье
 Скачать 7.85 Mb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Ижевский государственный технический университет имени М. Т. Калашникова» Факультет Приборостроительный Кафедра «Радиотехника» Работа защищена с оценкой «____________» Дата______________ Подпись__________/___________ Лабораторная работа №4 по дисциплине: «Цифровая обработка сигналов» на тему «Исследование быстрого преобразования Фурье» Вариант 6 Выполнил: студент гр. Б20-761-1 Малькин А.С. Дата, подпись Проверил: старший преподаватель Белоусов А.Ю. Ижевск, 2023 Цель работы: изучение быстрого преобразования Фурье, влияние весовых функций и объема выборки на разрешающую способность, фильтрующие свойства весовых функций, обратного преобразования Фурье. Средства, используемые при выполнении лабораторной работы: Лабораторная работа выполняется на персональном компьютере в среде «MATLAB 7.1» и «SIMULINK». Исходные данные: Эксперимент 1, задание 2,3: Весовые функции: Ханна, Блэкмана; Величина буфера: 64; Частота сигнала, Гц: 1000, 1025, 1050, 1075, 1100, 1125. Эксперимент 2, задание 2: Весовые функции: Хэмминга, Кайзера. Ход работы Собираем схему №1: 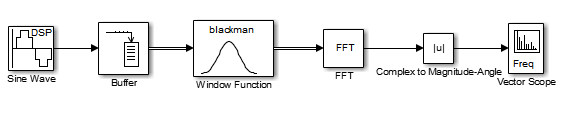 Рисунок 1 – Схема модели для задания 1 Эксперимент 1: Изучение БПФ, эффектов просачивания, влияние весовых функций на просачивание, представление спектра для реального и комплексного сигналов. Задание 1: Зададим у генератора синусоидального сигнала амплитуду 1 вольт, частоту 1КГц, частоту дискретизации 8КГц выходной сигнал как реальный. Установим величину буфера равной 64. Выберем весовую функцию прямоугольную. Изменим значение выходного сигнала генератора синусоиды на комплексный. Получим спектрограмму для различного представления по оси частот (0 –fд, - fд/2 - fд/2, 0 - fд/2). 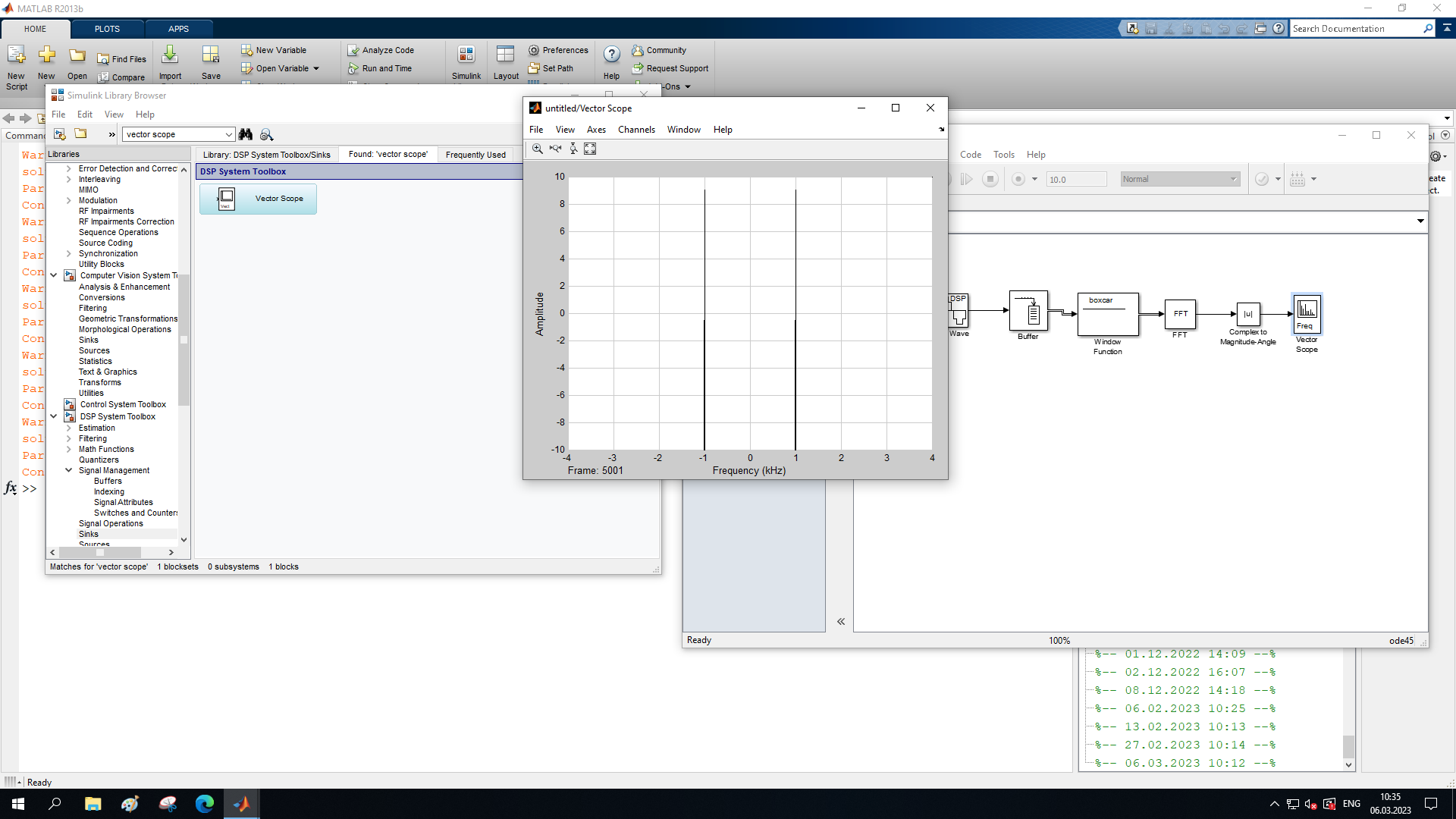 Рисунок 2 – спектрограмма для представления по оси частот (- fs/2 ; fs/2) 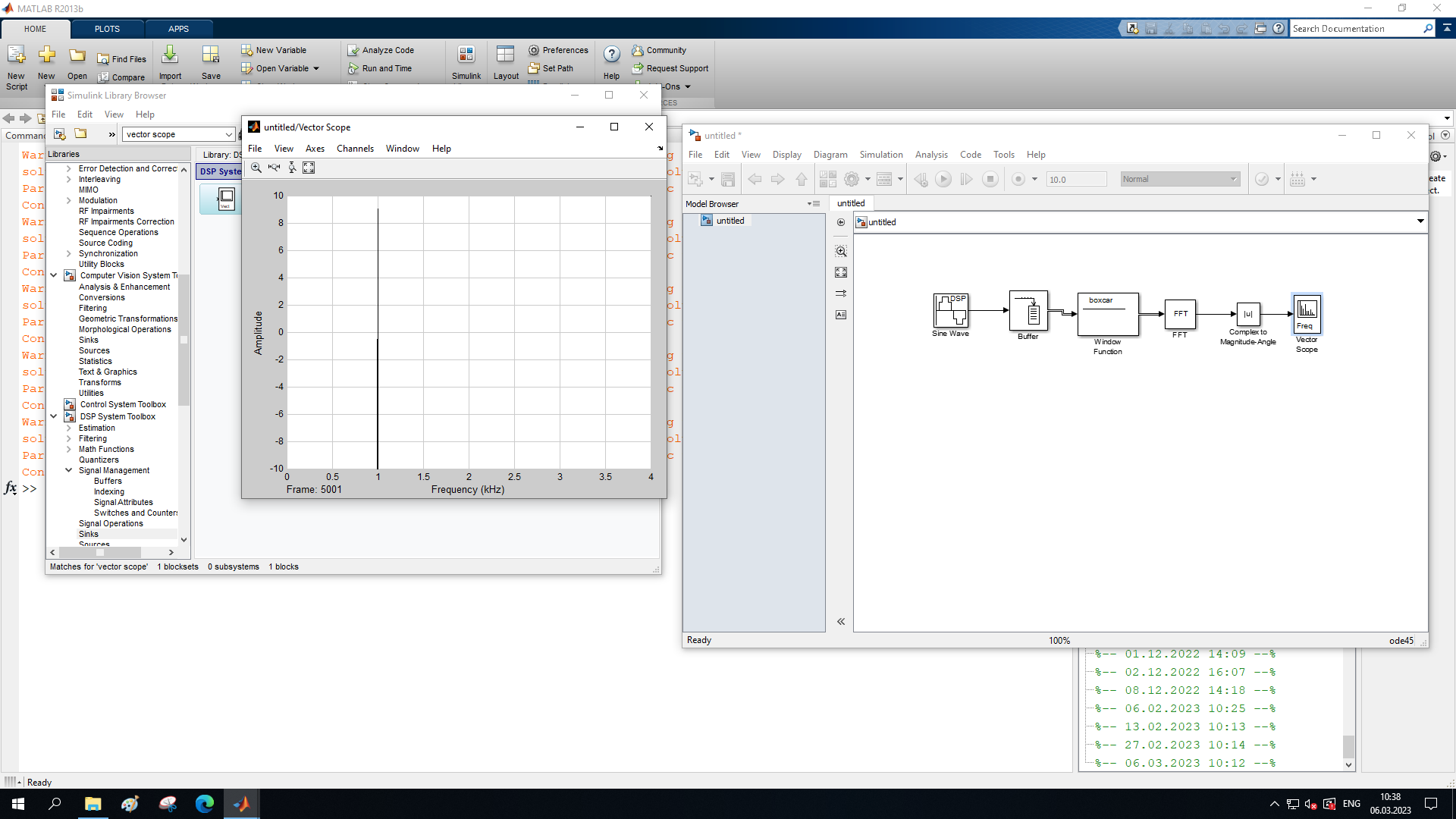 Рисунок 3 – Спектрограмма для представления по оси частот (0; fs/2) 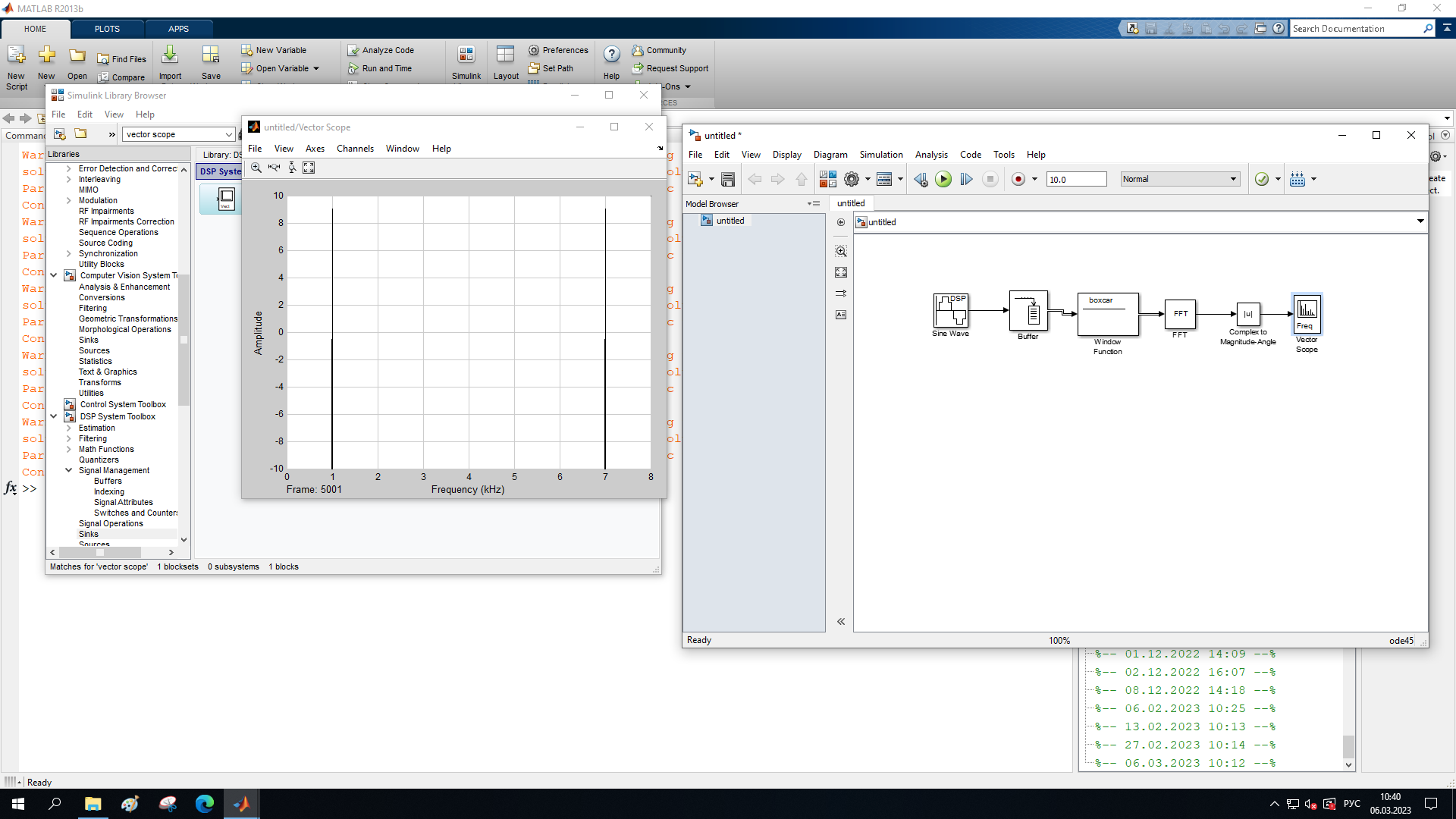 Рисунок 4 – Спектрограмма для представления по оси частот (0; fs) На сигналы с частотой ωх ≠ ωk откликаются два соседних канала на уровне главных лепестков их частотных характеристик, а на уровне боковых лепестков откликаются все каналы ДПФ, сигнал в этом случае проецируется на все бины ДПФ, т.е. присутствует на выходах всех каналов. Это явление называют размыванием спектра, дроблением или просачиванием спектра между каналами. При этом затруднительны однозначное обнаружение сигнала и оценка его параметров (амплитуды, частоты и фазы). Изменяем значение выходного сигнала генератора синусоиды на комплексный. Получим спектрограмму для различного представления по оси частот (0 –fд, - fд/2 - fд/2, 0 - fд/2). 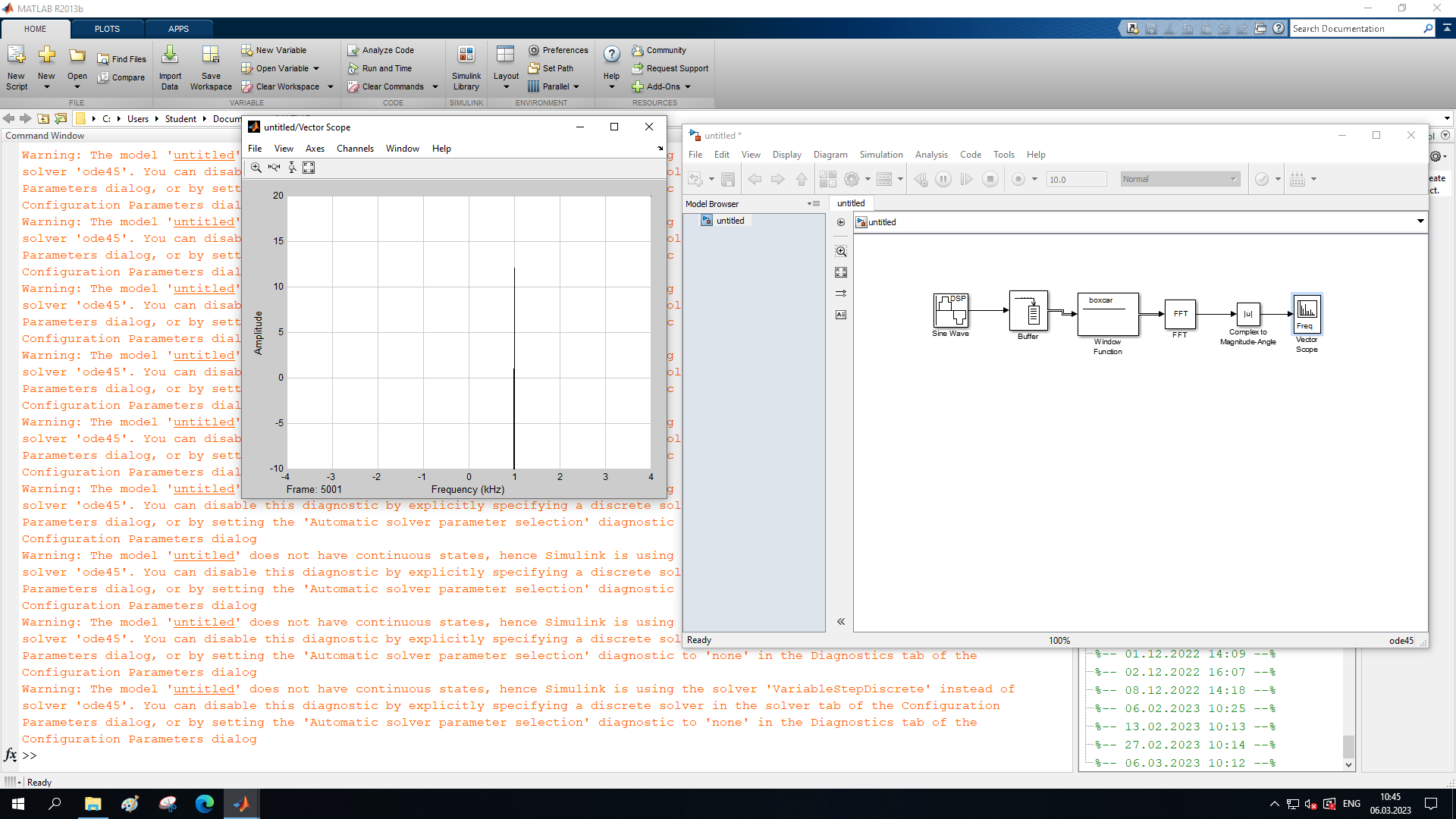 Рисунок 5 – Спектрограмма для представления по оси частот (- fs/2 ; fs/2) 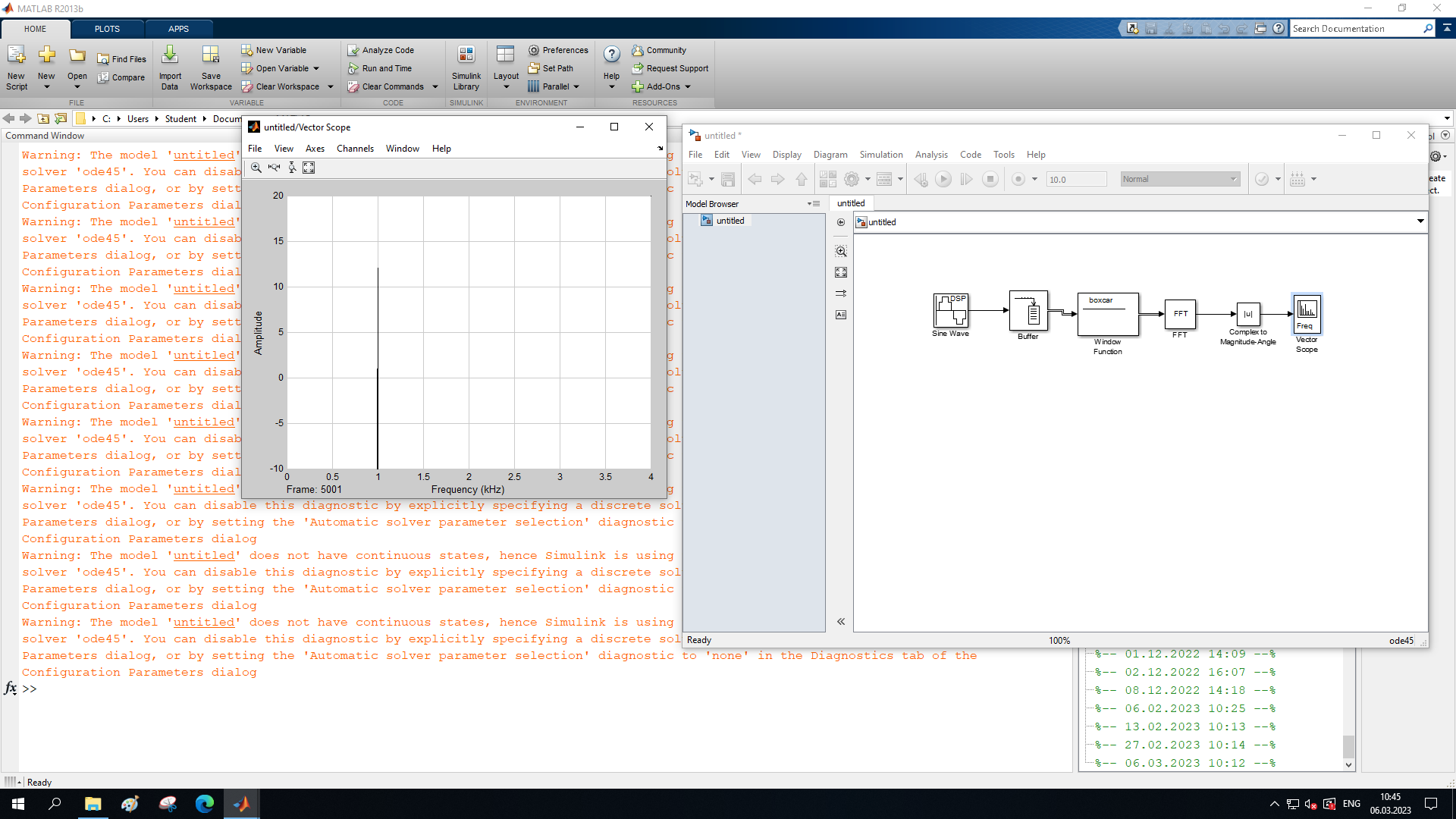 Рисунок 6 – Спектрограмма для представления по оси частот (0; fs/2) 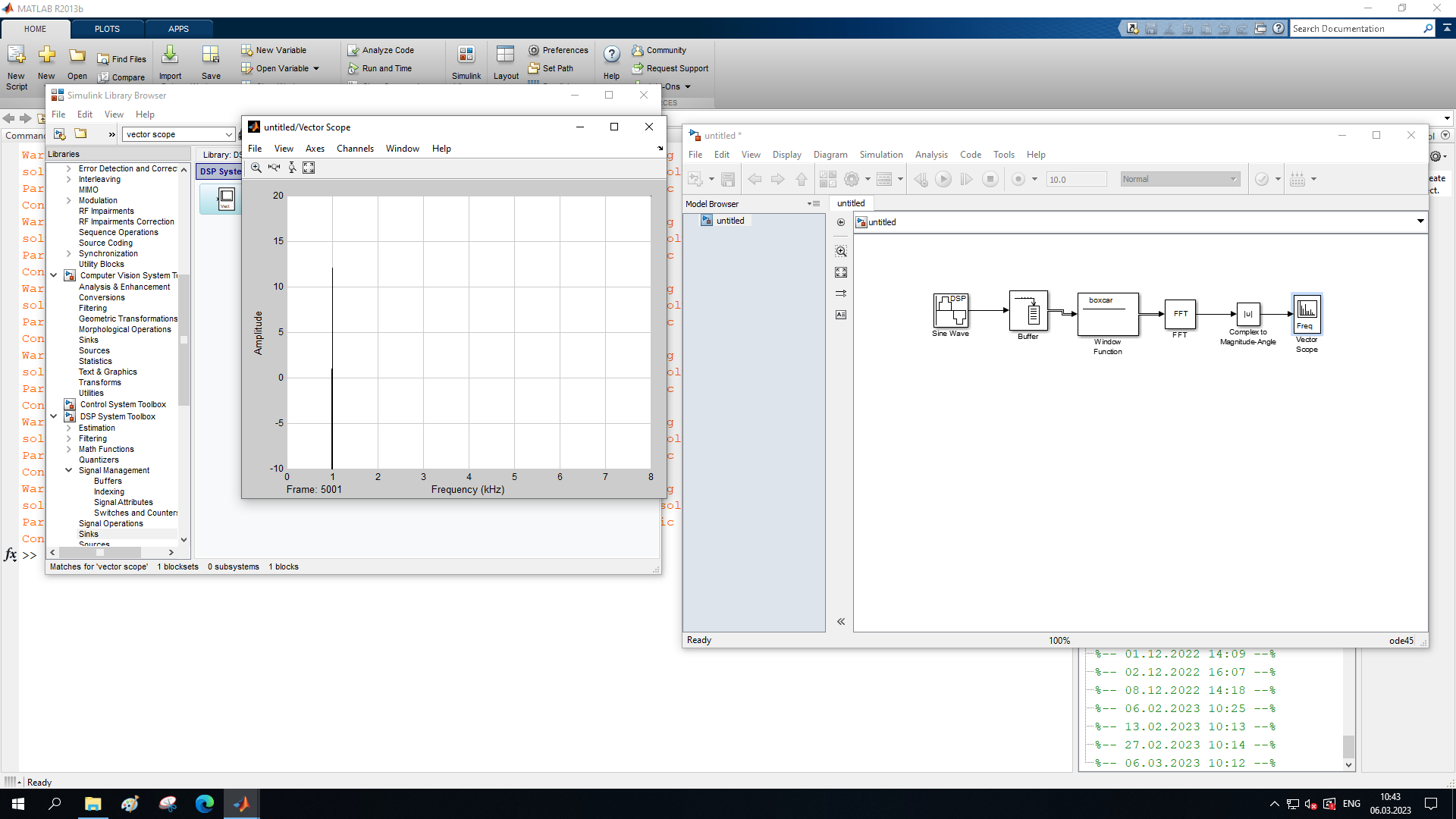 Рисунок 7 – Спектрограмма для представления по оси частот (0; fs) Для комплексного выходного сигнала генератора зададим отрицательную частоту 1КГц и для представления оси частот для векторного осциллографа (- fд/2 – fд/2) получим спектрограмму. 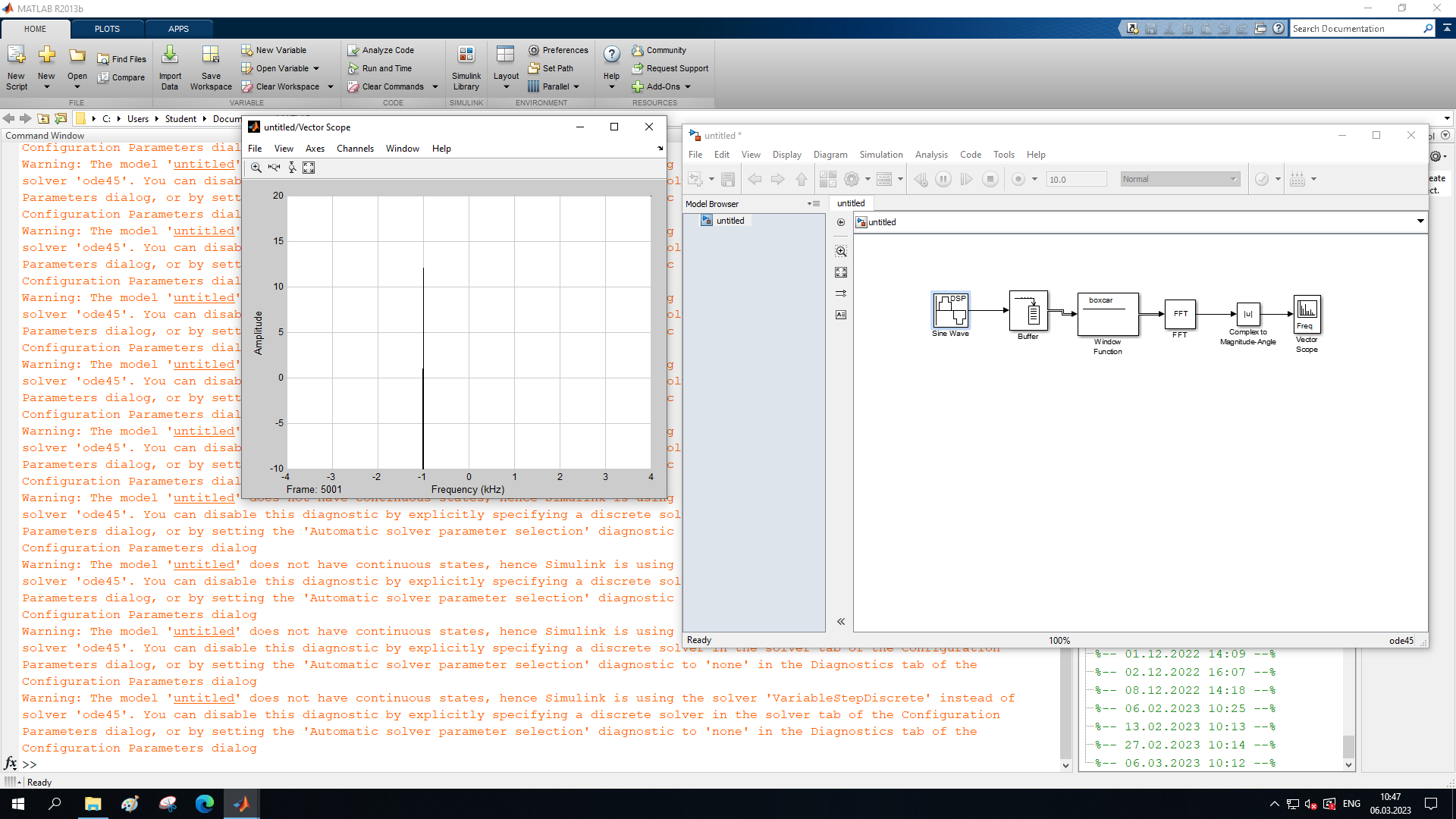 Рисунок 8 – Спектрограмма для отрицательной частоты 1кГц Однозначное разрешение комплексного гармонического сигнала анализатором спектра с прямоугольной весовой функцией имеет место только на частотах ωх=ωk, совпадающих с частотами анализа ДПФ, когда на интервале анализа укладывается целое число периодов сигнала: Tа=(N–1)Tд=kT. В этом случае сигнал присутствует только на выходе одного канала или, как говорят, проецируется на 1 бин ДПФ. При этом возможно однозначное обнаружение и оценка параметров сигнала по вычисленному значению ДПФ X (jωk). Задание 2: Для буфера равным 64, представления оси частот для векторного осциллографа (-fд/2 – fд/2) и функции Ханна получим спектрограммы для значения частот 1000, 1025, 1050, 1075, 1100, 1125 Гц. На рисунке 9 представлены спектрограммы сигналов функции Ханна при частоте 1000 Гц и 1025Гц. 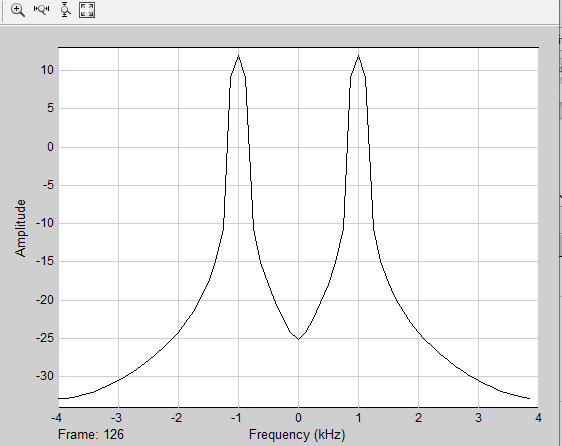  Рисунок 9 - Спектрограмма сигнала при частоте 1000 Гц (слева) и 1025 Гц (справа) соответственно На рисунке 10 представлены спектрограммы сигналов функции Ханна при частоте 1050 Гц и 1075Гц. 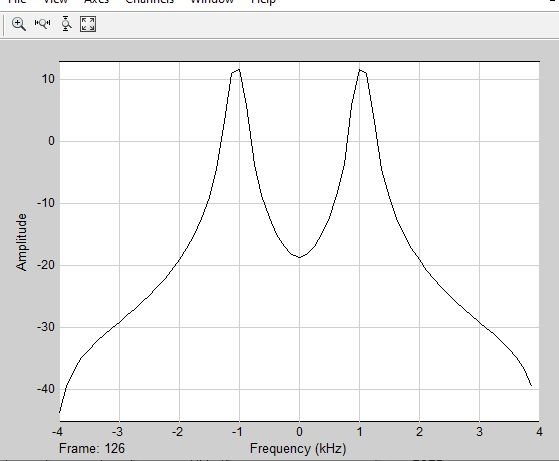 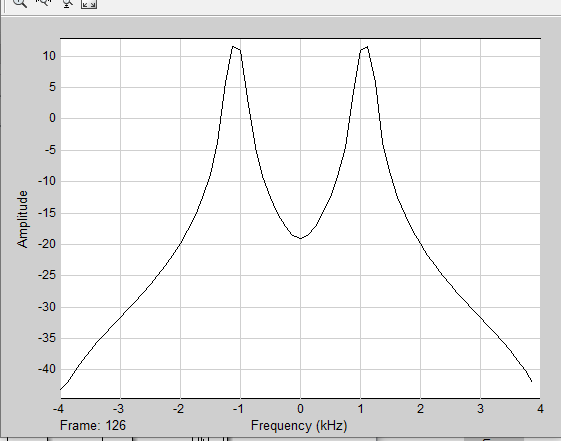 Рисунок 10 - Спектрограмма сигнала при частоте 1050 Гц (слева) и 1075 Гц (справа) соответственно На рисунке 11 представлены спектрограммы сигналов функции Ханна при частоте 1100 Гц и 1125 Гц 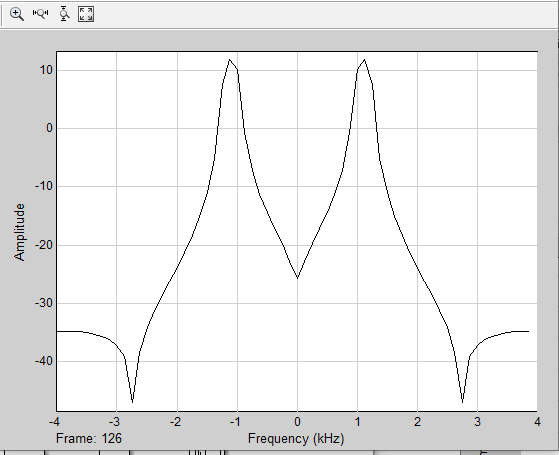 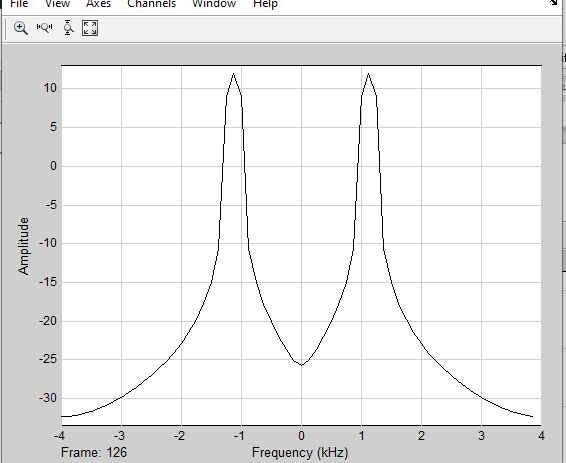 Рисунок 11 - Спектрограмма сигнала при частоте 1100 Гц (слева) и 1125 Гц (справа) соответственно Задание 3: Повторим задание 2 для весовой функции Блэкмана На рисунке 12 представлены спектрограммы сигналов функции Блэкмана при частоте 1000 Гц и 1025Гц. 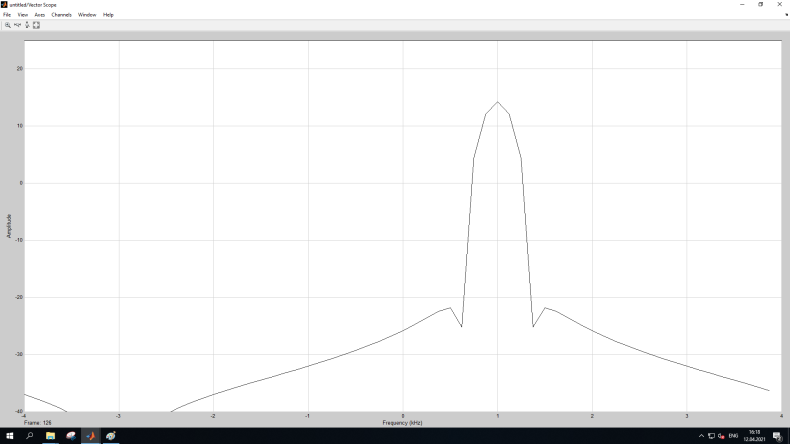 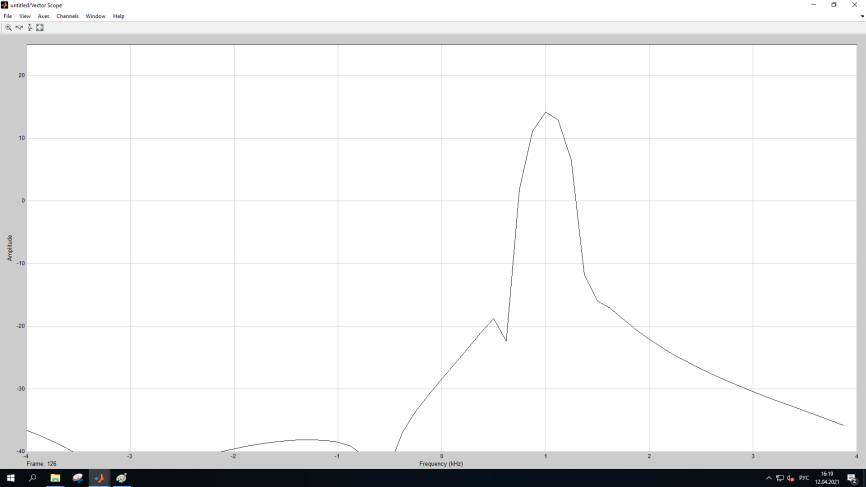 Рисунок 12 – Спектрограмма сигнала при частоте 1000 Гц (сверху) и 1025 Гц (снизу) соответственно На рисунке 13 представлены спектрограммы сигналов функции Блэкмана при частоте 1050 Гц и 1075 Гц 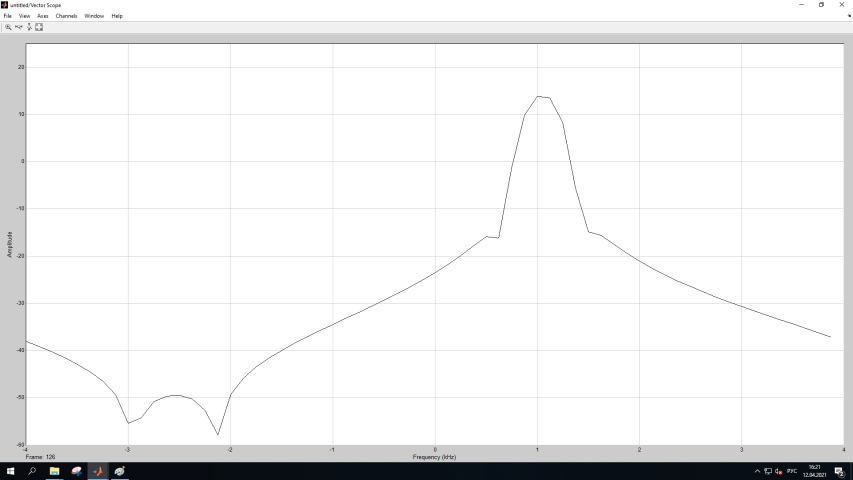 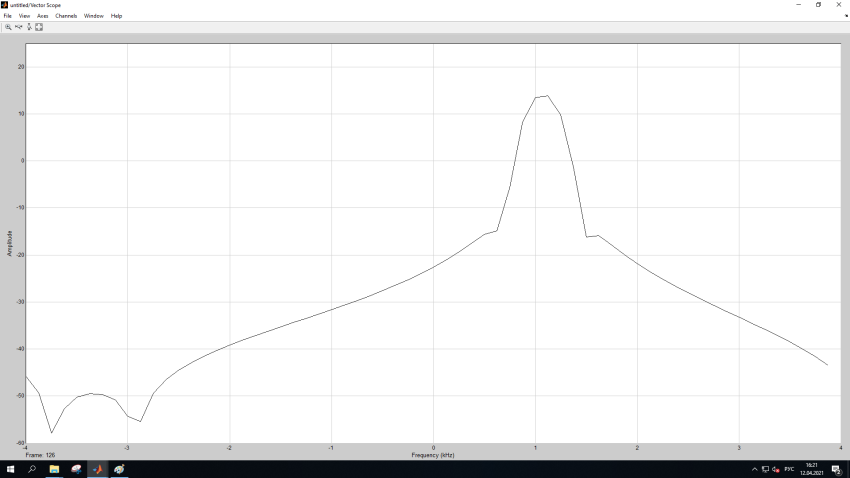 Рисунок 13 – Спектрограмма сигнала при частоте 1050 Гц (сверху) и 1075 Гц (снизу) соответственно На рисунке 14 представлены спектрограммы сигналов функции Блэкмана при частоте 1100 Гц и 1125 Гц 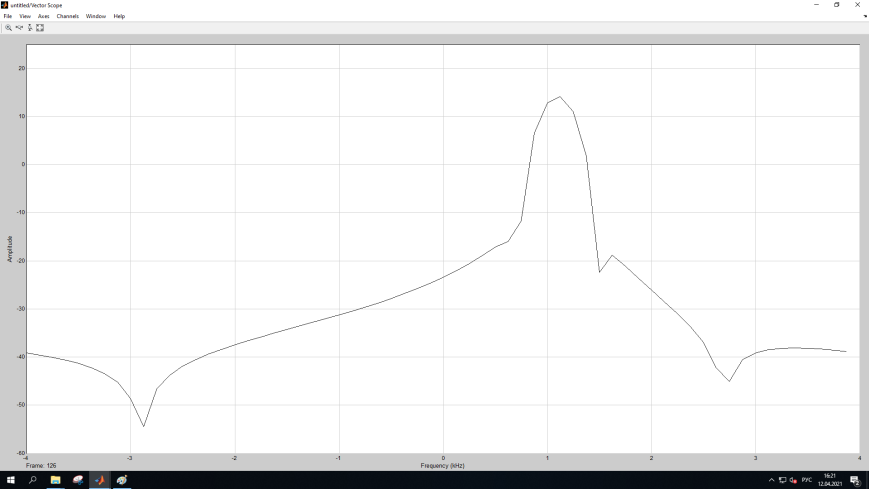 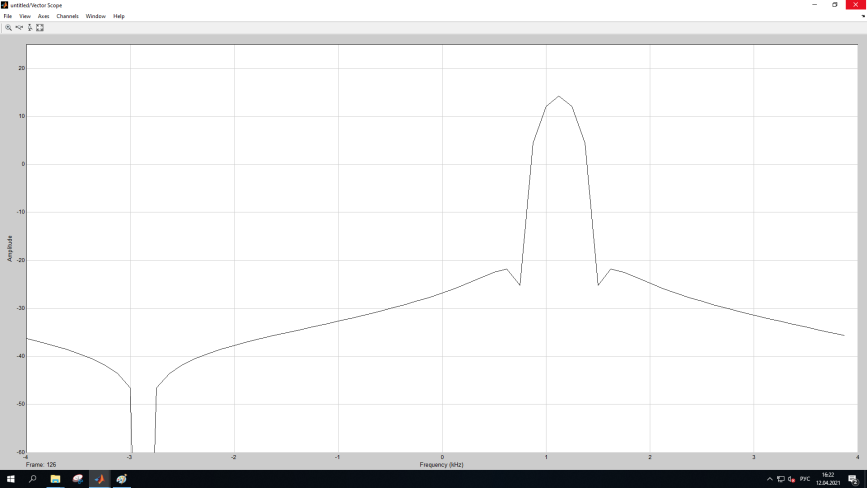 Рисунок 14 – Спектрограмма сигнала при частоте 1100 Гц (снизу) и 1125 Гц (сверху) соответственно Эксперимент 2: Изучение разрешающей способности от времени анализа (объема выборки) и используемой весовой функции. Задание 1: Соберем схему, приведенную на рисунке 15 Зададим частоты генераторов 1100Гц и 1200Гц, амплитуду 1 вольт, частоту дискретизации 8КГц, весовую функцию прямоугольную, представления оси частот для векторного осциллографа (-fд/2 – fд/2), время моделирования 10 секунд. Задавая величину буфера 64, 128, 512,1024, 16384, 65536 получим спектрограммы. 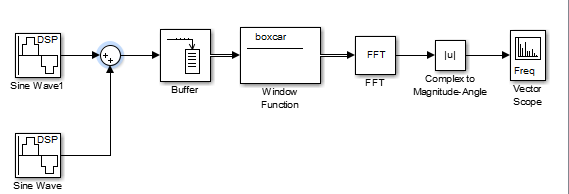 Рисунок 15 – Схема модели для задания 2 На рисунке 16 представлены спектрограммы сигналов Прямоугольной функции при величине буфера 64 и 128 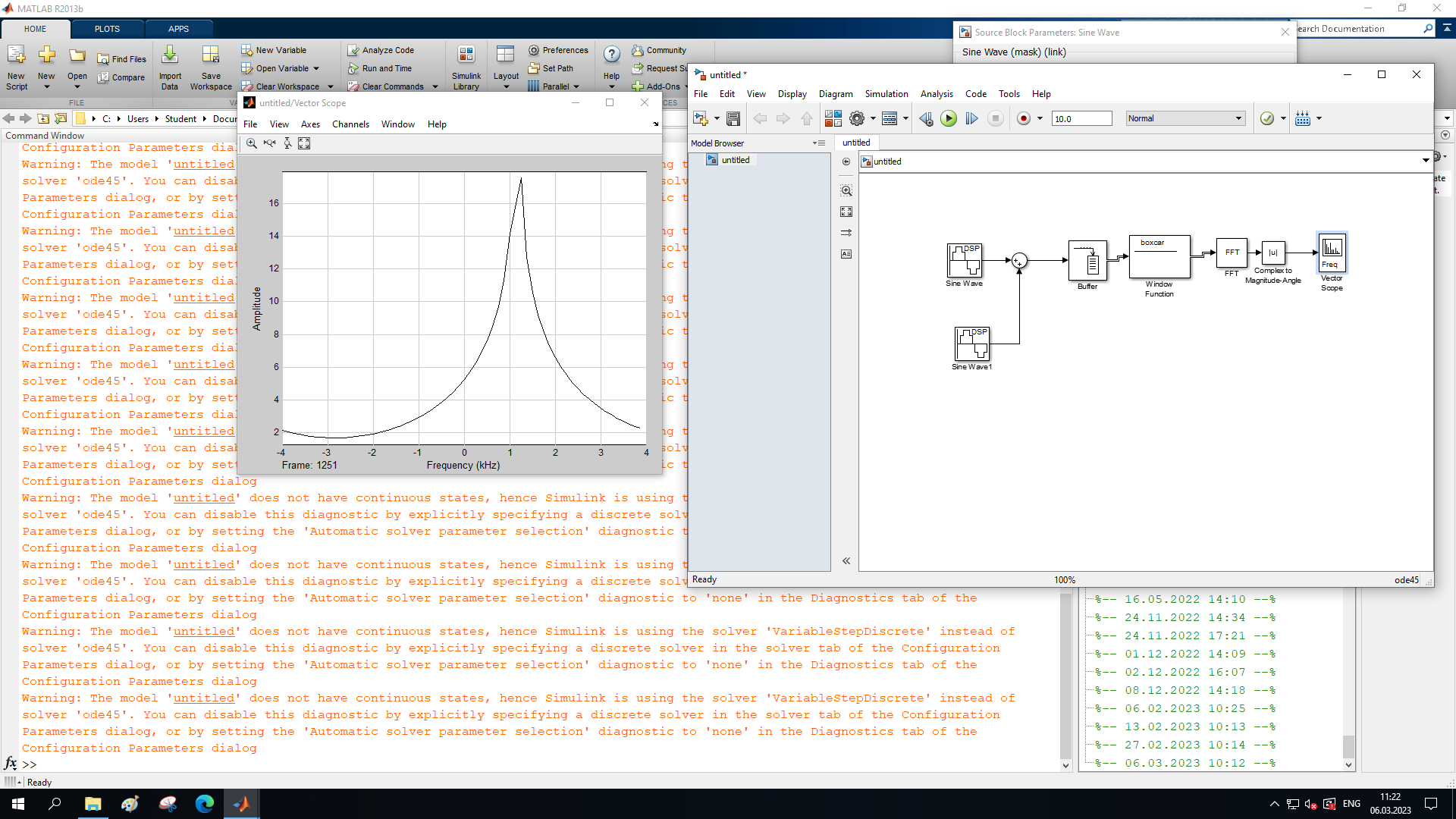 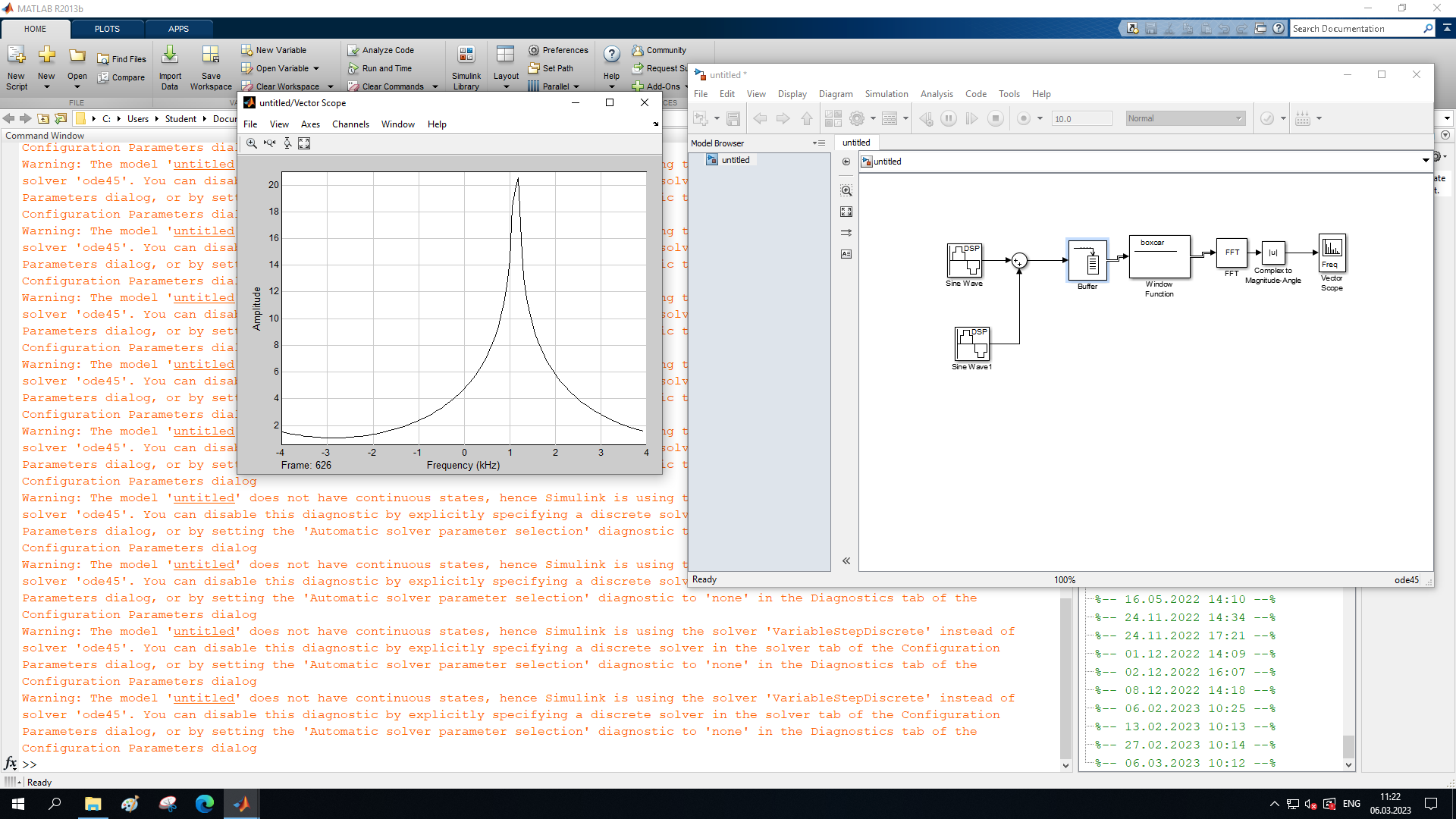 Рисунок 16 – Спектрограмма сигнала при величине буфера 64 (сверху) и 128 (снизу) соответственно На рисунке 17 представлены спектрограммы сигналов Прямоугольной функции при величине буфера 512и 1024 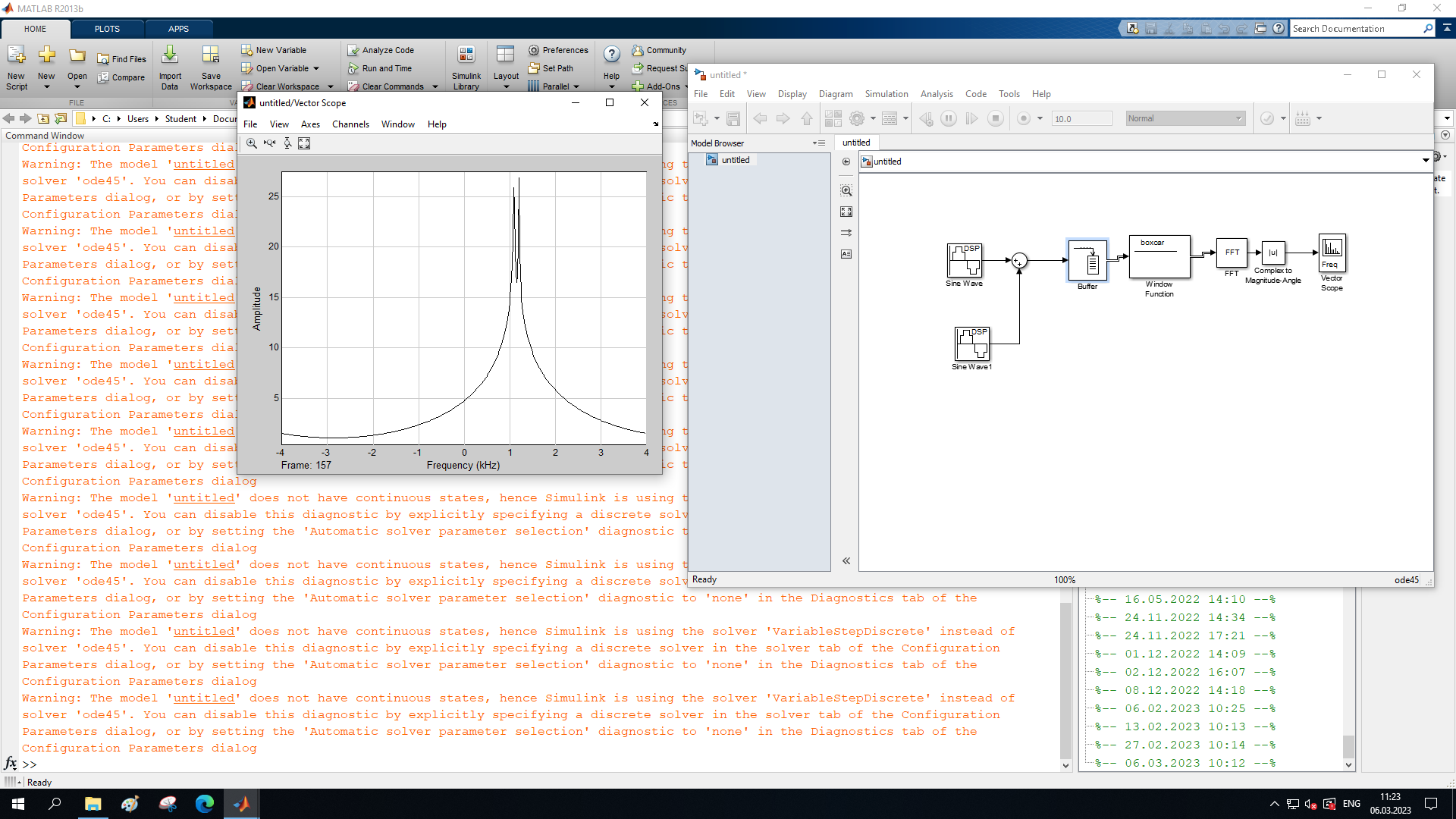 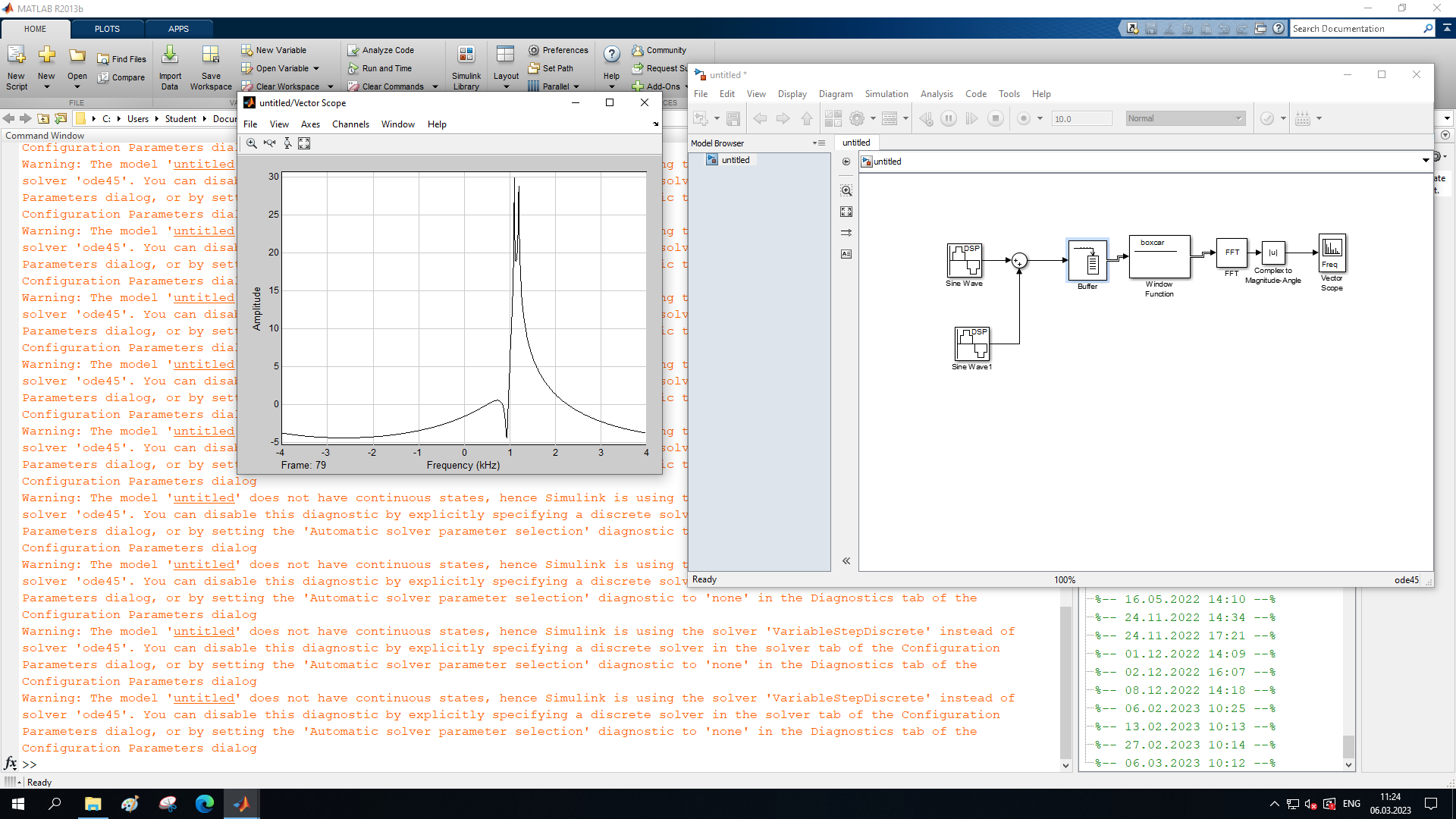 Рисунок 17 – Спектрограмма сигнала при величине буфера 512 (сверху) и 1024 (снизу) соответственно На рисунке 18 представлены спектрограммы сигналов Прямоугольной функции при величине буфера 16384 и 65536 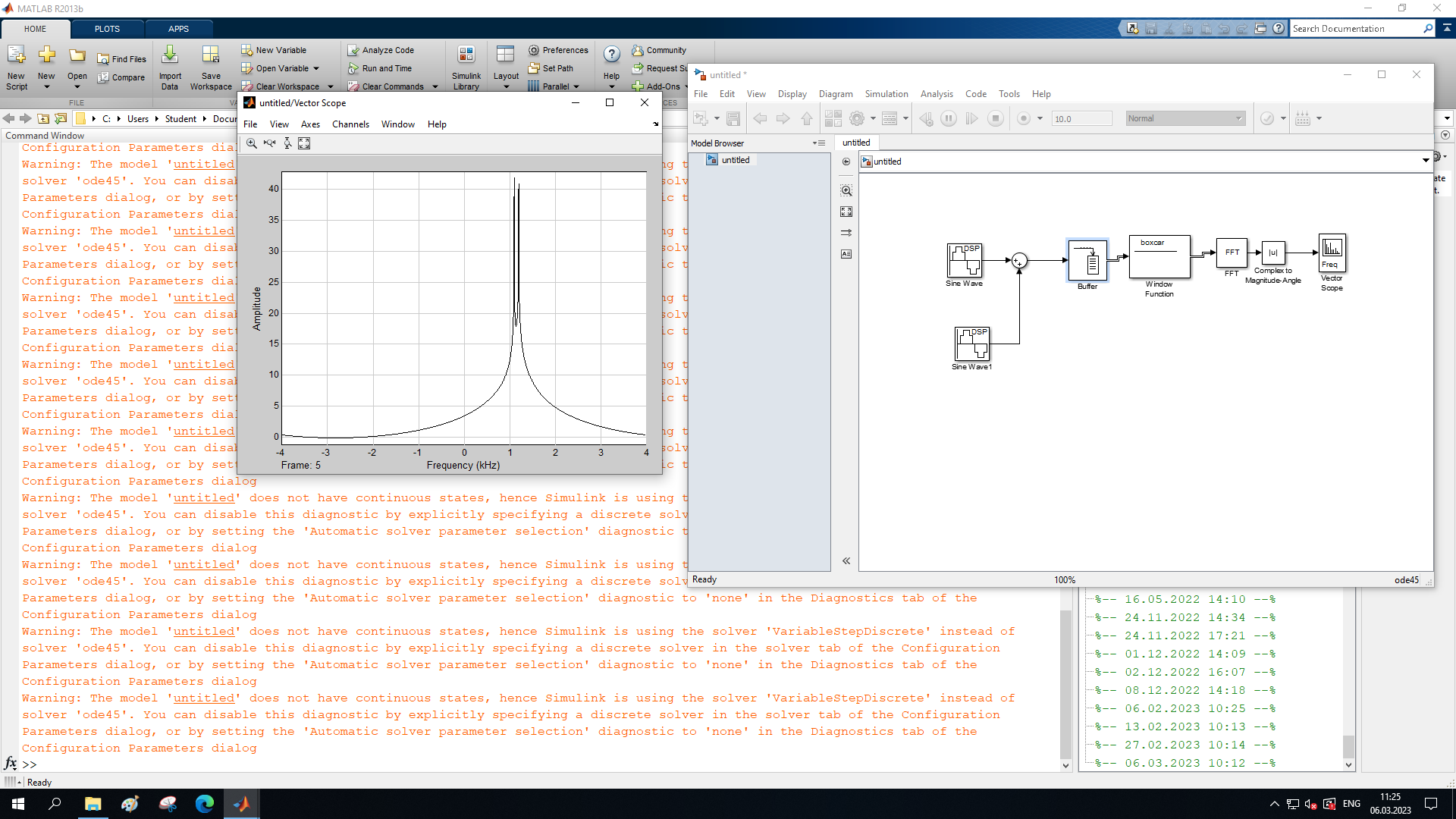 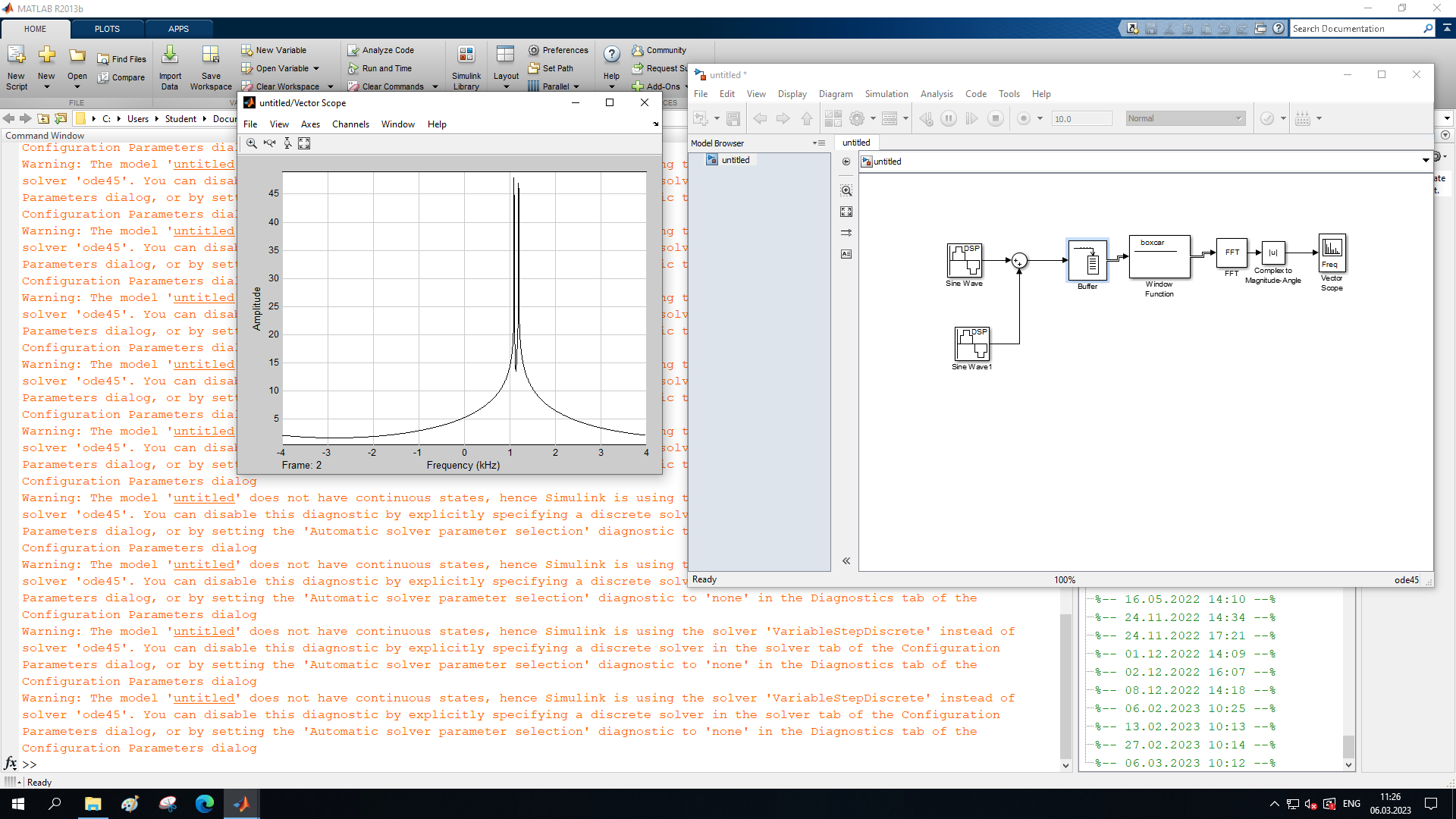 Рисунок 18 – Спектрограмма сигнала при величине буфера 16384 (сверху) и 65536 (снизу) соответственно Задание 2: Повторим задание 1 для весовой функции Блэкмана и Кайзера. На рисунке 19 представлены спектрограммы сигналов функции Кайзера при величине буфера 64 и 128   Рисунок 19 – Спектрограмма сигнала при величине буфера 64 (слева) и 128 (справа) соответственно На рисунке 20 представлены спектрограммы сигналов функции Кайзера при величине буфера 512 и 1024  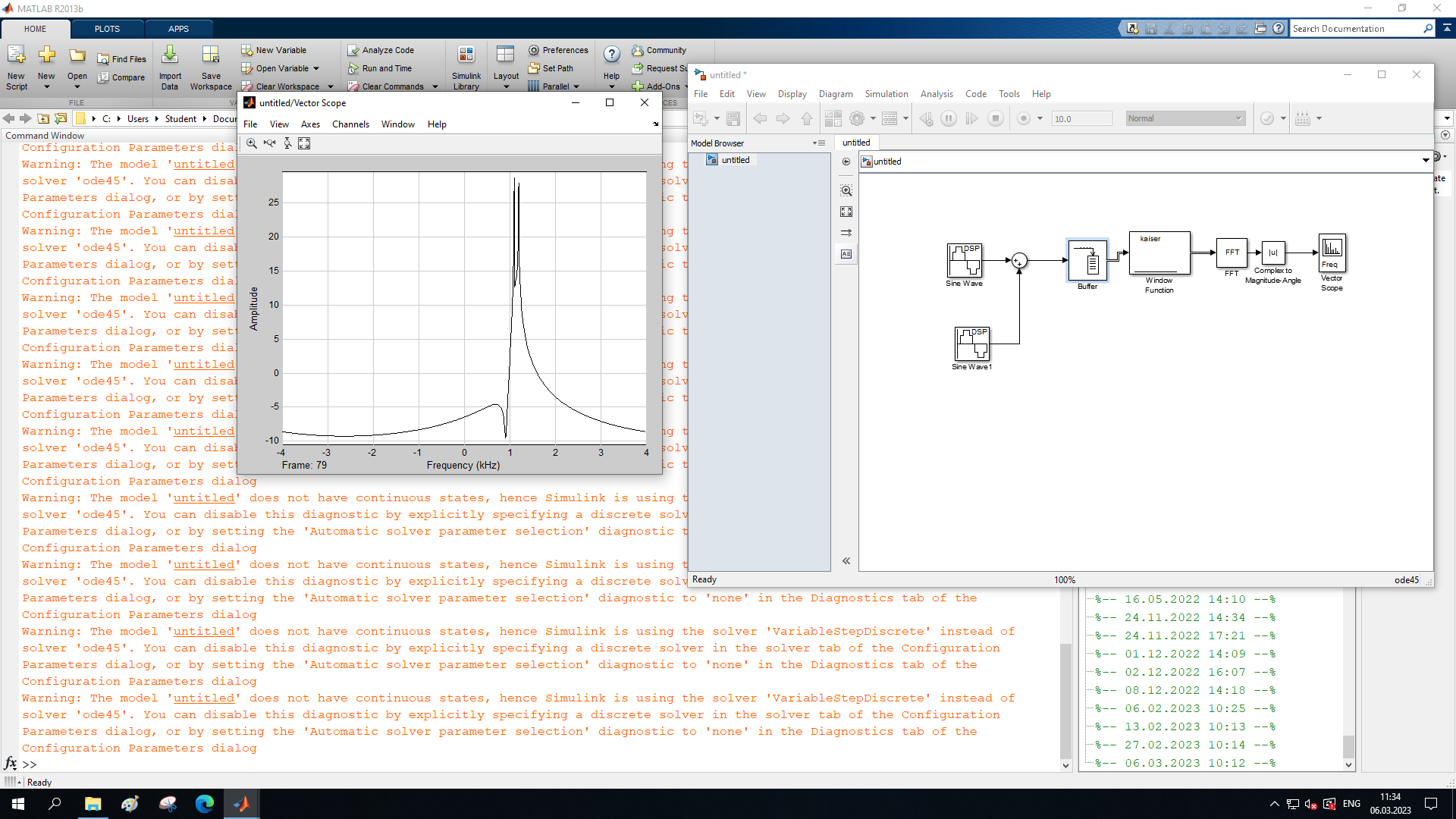 Рисунок 20 – Спектрограмма сигнала при величине буфера 512 (слева) и 1024 (справа) соответственно На рисунке 21 представлены спектрограммы сигналов функции Кайзера при величине буфера 16384 и 65536  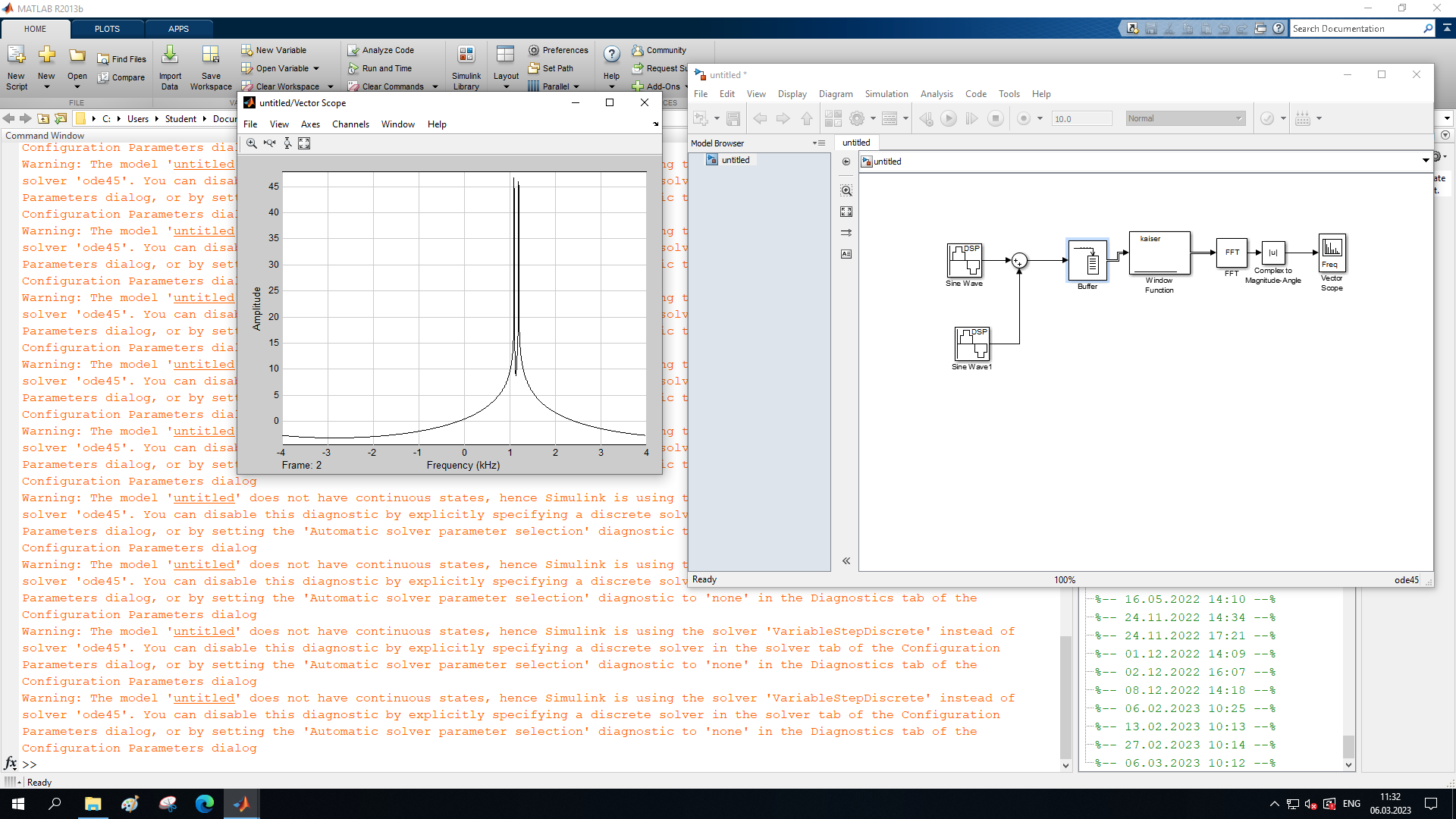 Рисунок 21 – Спектрограмма сигнала при величине буфера 16384 (слева) и 65536 (справа) соответственно На рисунке 22 представлены спектрограммы сигналов функции Блэкмана при величине буфера 64 и 128 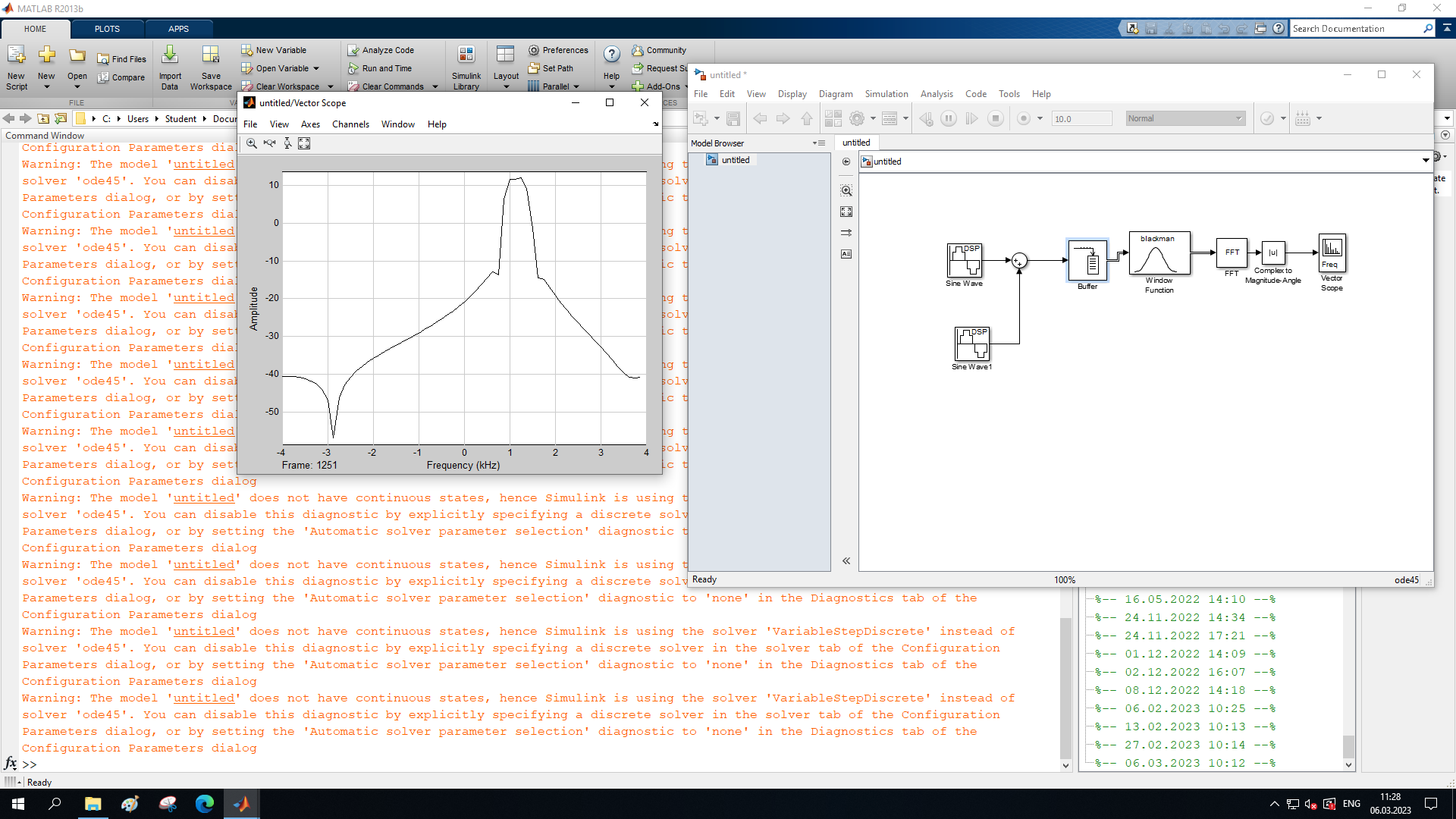 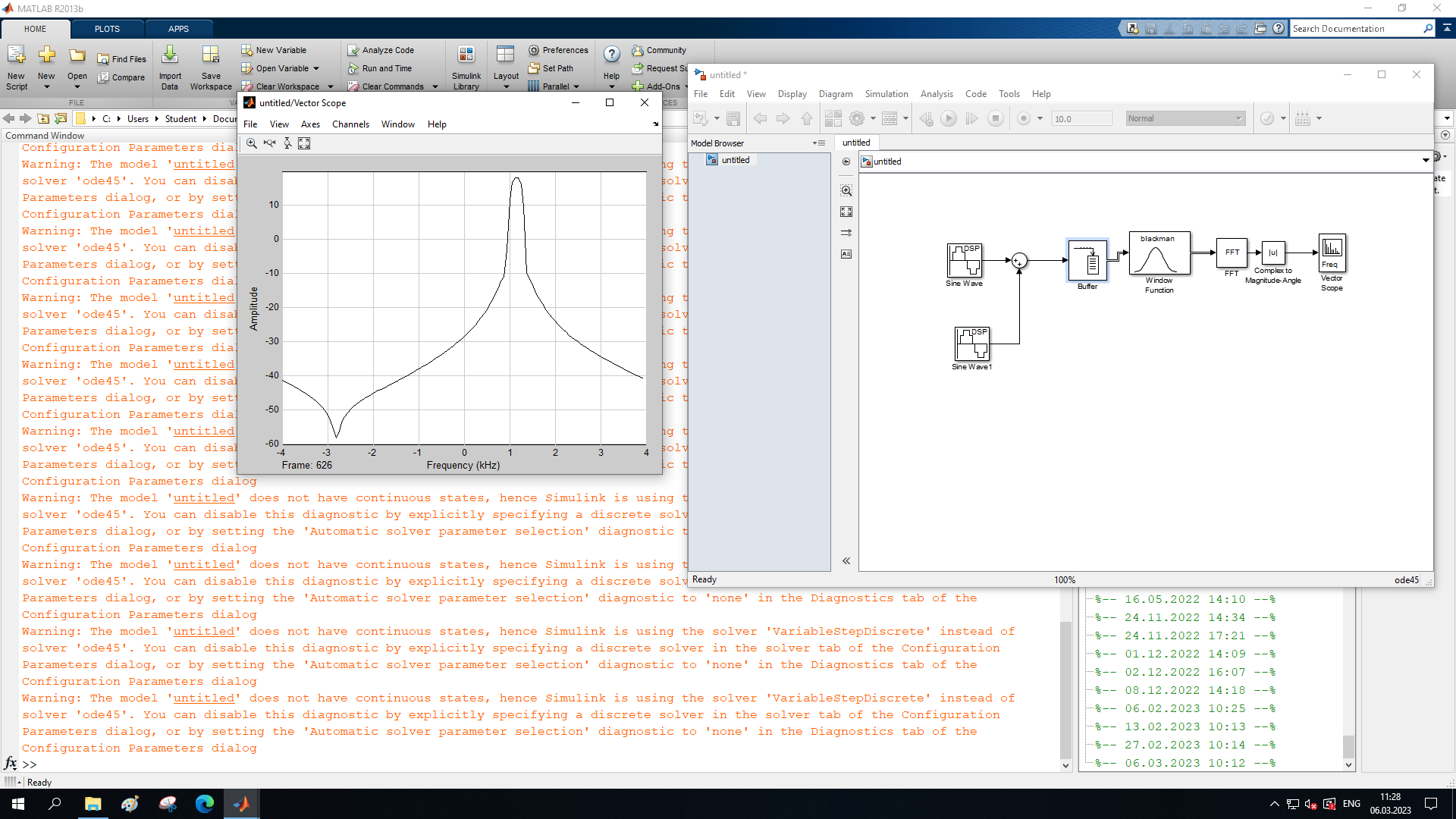 Рисунок 22 – Спектрограмма сигнала при величине буфера 64 (слева) и 128 (справа) соответственно На рисунке 23 представлены спектрограммы сигналов функции Блэкмана при величине буфера 512 и 1024 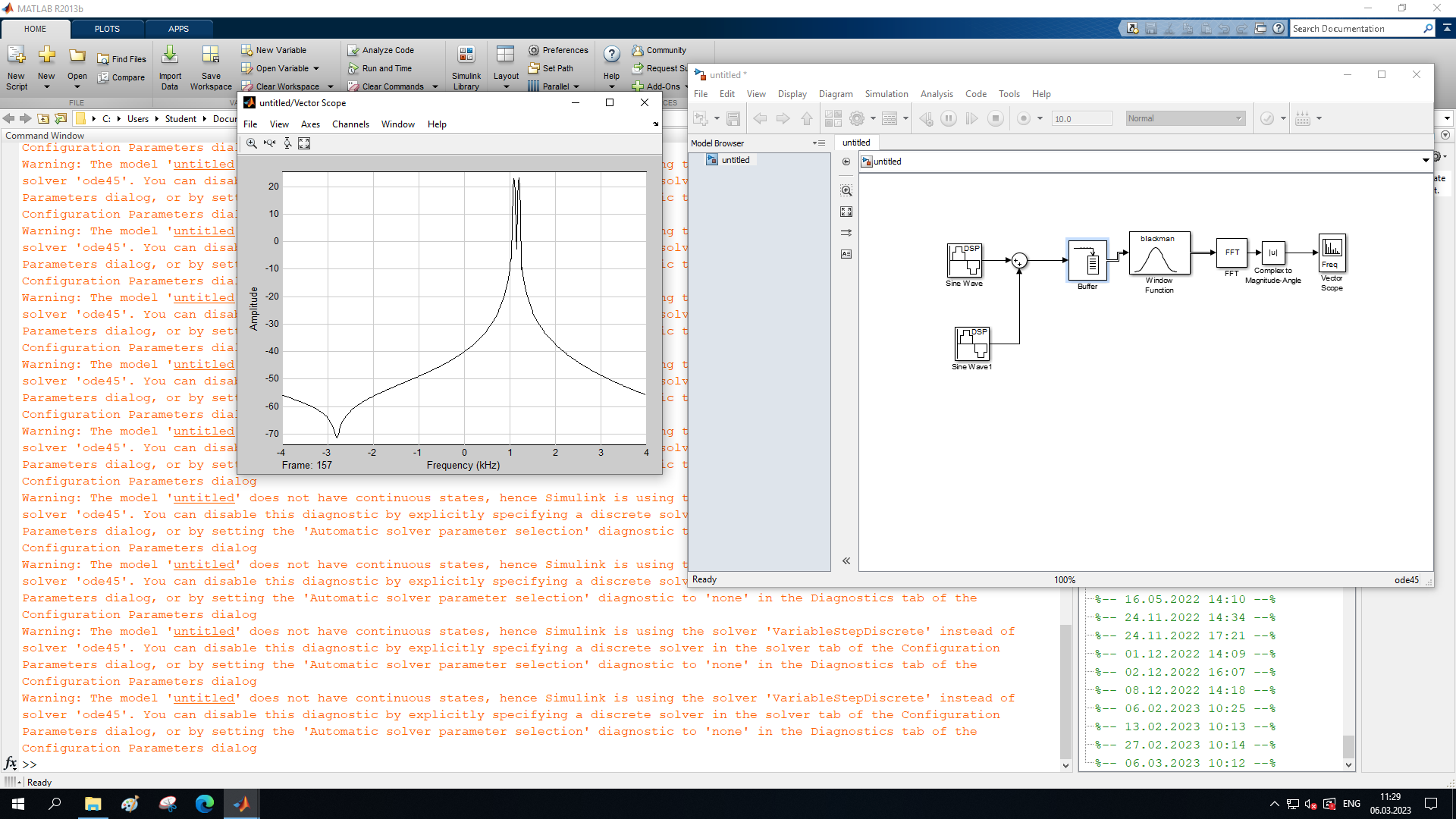 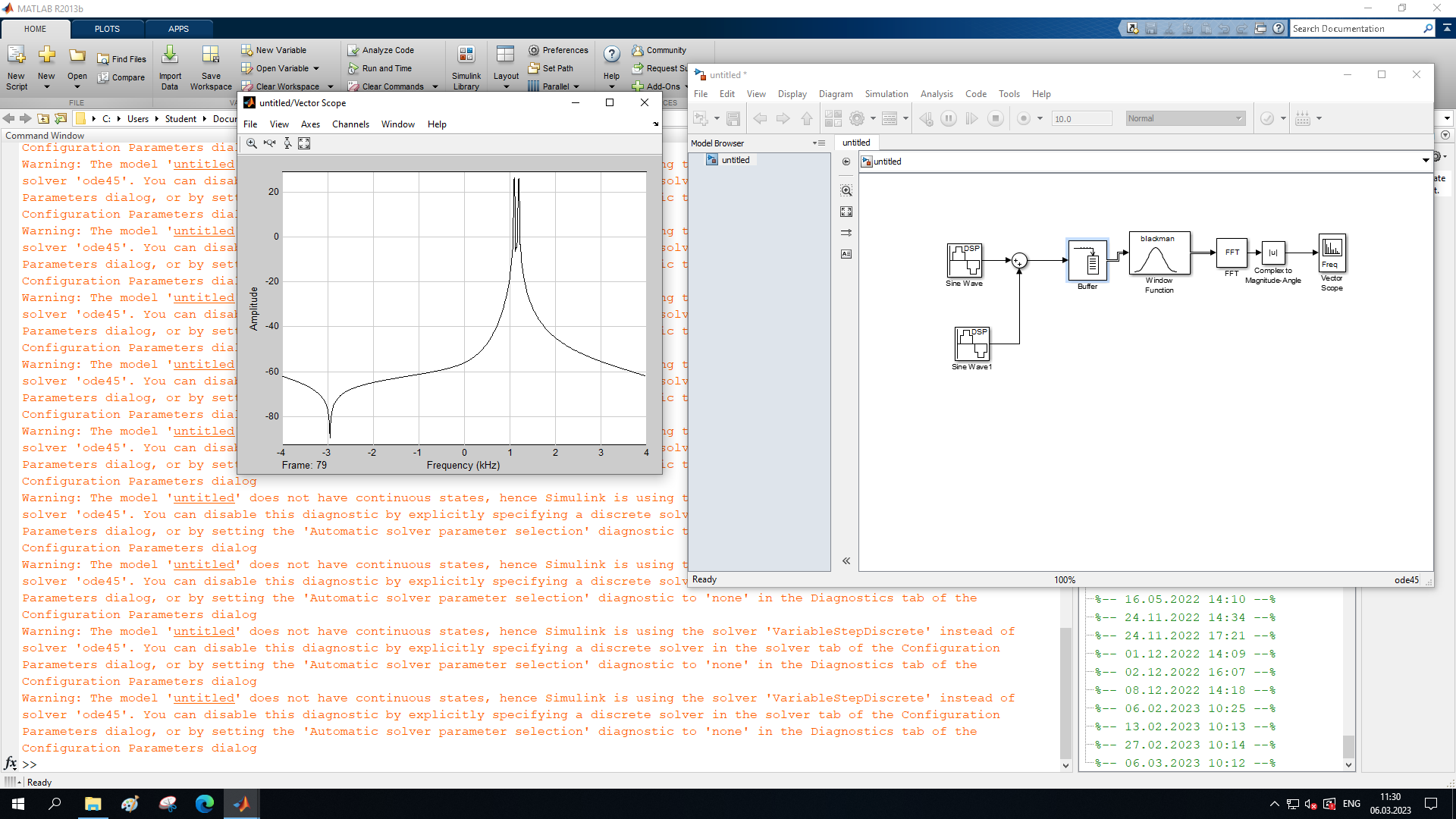 Рисунок 23 – Спектрограмма сигнала при величине буфера 512 (сверху) и 1024 (снизу) соответственно На рисунке 24 представлены спектрограммы сигналов функции Блэкмана при величине буфера 16384 и 65536  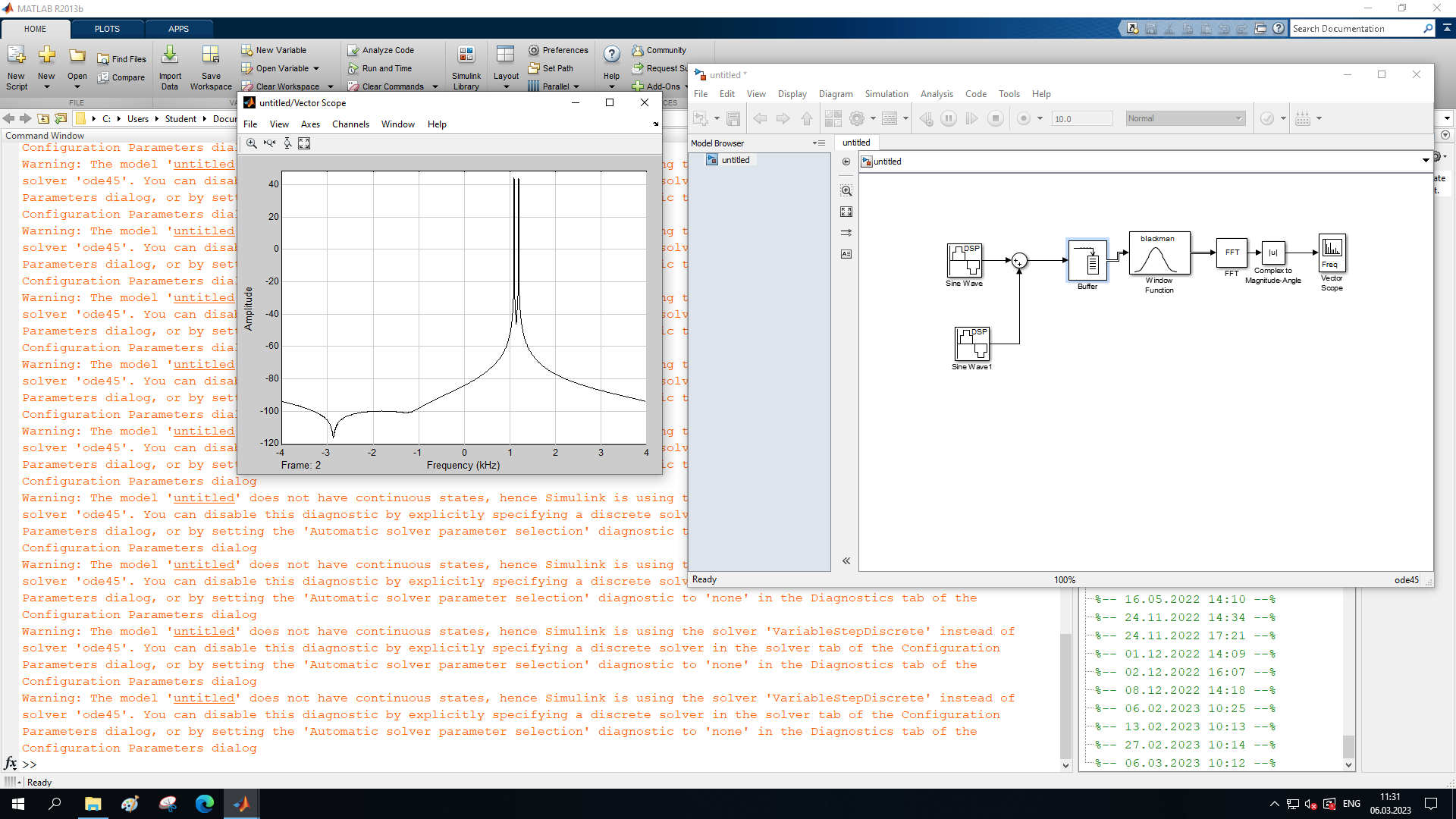 Рисунок 24 – Спектрограмма сигнала при величине буфера 16384 (сверху) и 65536 (снизу) соответственно; Использование разных весовых функции приводит к изменению разрешающей способности анализатора спектра. Высокий уровень боковых лепестков и обусловленное им сильное взаимное влияние каналов анализатора спектра является основным недостатком прямоугольной весовой функции. Особенно оно существенно при разрешении нескольких одновременно действующих сигналов или при наличии сосредоточенных помех, существенно искажающих результаты анализа. Эти недостатки преодолеваются при использовании весовых функций, имеющих меньший уровень боковых лепестков. Однако при этом возрастает ширина главного лепестка Δfгл = DfД/N, где D > 2 (D – де-фактор непосредственной связи с весовой функцией). Это приводит к увеличению числа каналов с перекрывающимися главными лепестками частотных характеристик и ухудшению разрешающей способности анализатора спектра. Эксперимент 3: Изучение обратного преобразования Фурье. Соберем схему, приведенную на рисунке 25. Схема по сравнению со схемами, используемыми в экспериментах 1 и 2 дополнительно содержит блоки обратного преобразования Фурье, преобразования комплексного сигнала в реальный и блока, преобразующего данные из массива в последовательные отсчеты. Зададим частоты генераторов 1100Гц и 1200Гц, амплитуду 1 вольт, частоту дискретизации 8кГц, весовую функцию прямоугольную, представления оси частот для векторного осциллографа (- fд/2 - fд/2), время моделирования 10 секунд. 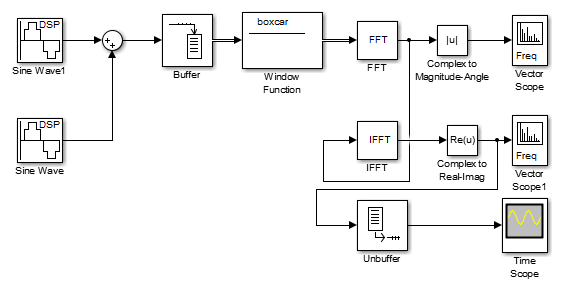 Рисунок 25 – Схема модели для задания 3 На рисунке 26 представлены спектрограммы и осциллограмма сигналов Прямоугольной функции после БПФ и ОБПФ при величине буфера 64.  Рисунок 26 – Спектрограмма сигнала после БПФ (левый), ОБПФ (правый) , осциллограмма (средний) соответственно Проводим моделирование данной схемы для функций Кайзера и Блэкмана. На рисунке 27 представлены спектрограммы и осциллограмма сигналов функции Кайзера после БПФ и ОБПФ при величине буфера 64. 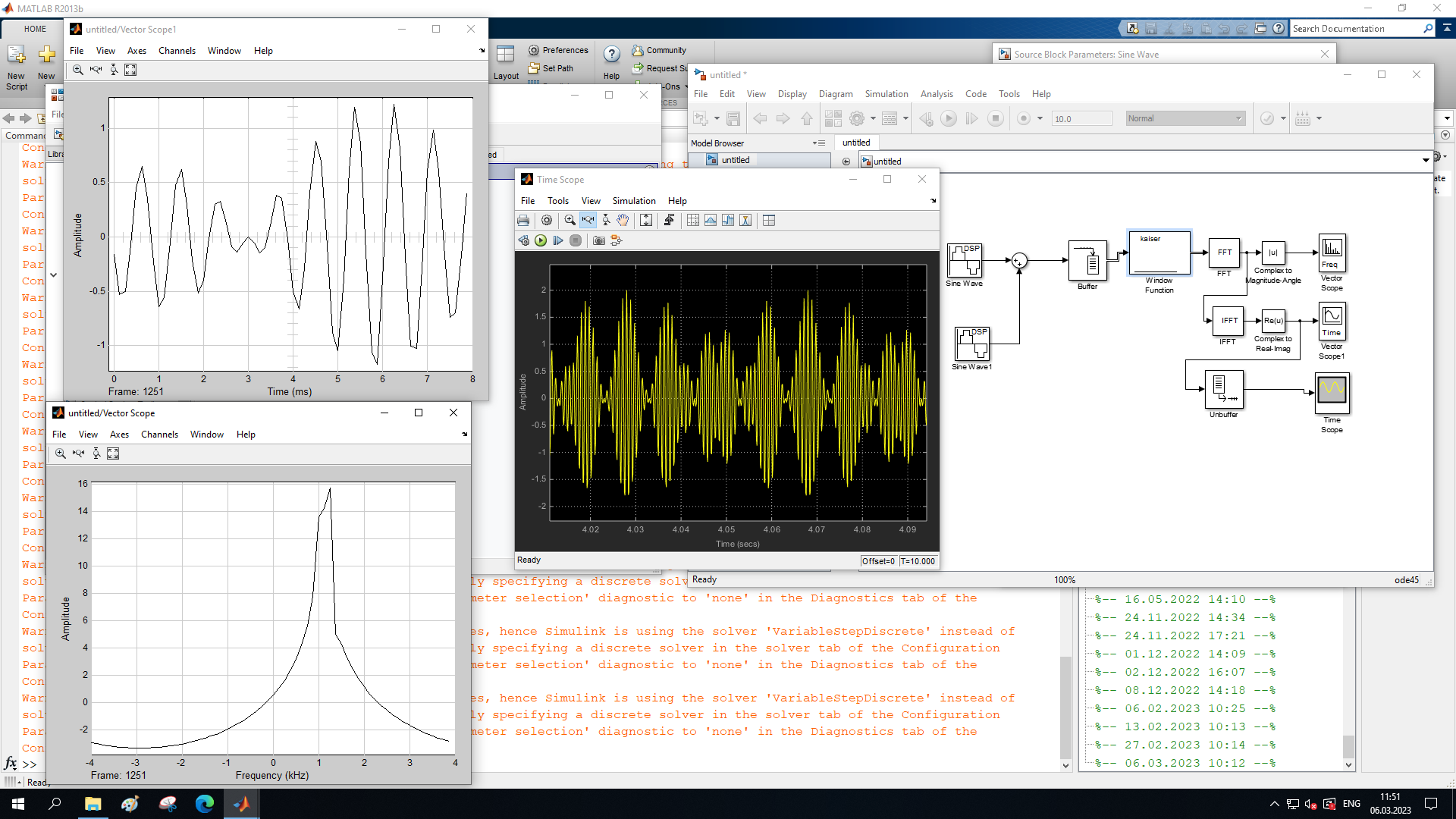 Рисунок 27 – Спектрограмма сигнала после БПФ (левый), ОБПФ (правый) , осциллограмма (средний) соответственно На рисунке 28 представлены спектрограммы и осциллограмма сигналов функции Блэкмана после БПФ и ОБПФ при величине буфера 64. 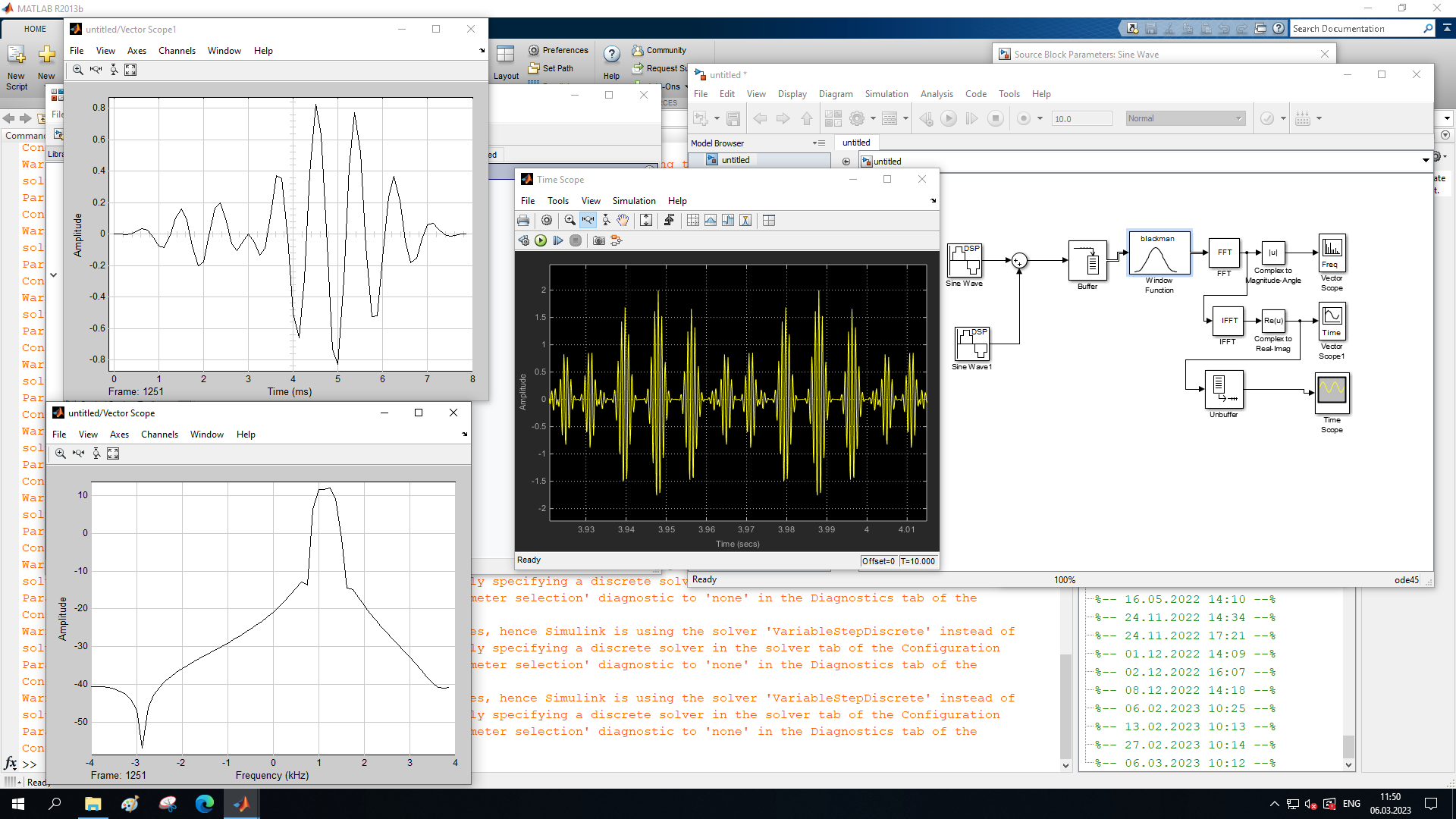 Рисунок 28 – Спектрограмма сигнала после БПФ (левый), ОБПФ (правый) , осциллограмма (средний) соответственно Вывод: В ходе лабораторной работы изучены БПФ, эффекты просачивания и влияние весовых функций на просачивание, изучена разрешающая способность используемых весовых функций в зависимости от времени анализа, рассмотрена процедура обратного преобразования Фурье. Контрольный вопрос: 3. Каковы основные параметры анализаторов спектра на основе ДПФ? Анализатор спектра на основе ДПФ В основе анализаторов спектра, использующих ДПФ, лежит базовая структура, приведенная на рис. 4. Она реализует базовые операции анализатора спектра – взвешивание и вычисление ДПФ. Ее выходом является вектор ДПФ входной в общем случае не ограниченной по длине последовательности x(n), усеченной весовой функцией w(n) конечной длины N:
k=0,1, …N–1. Здесь 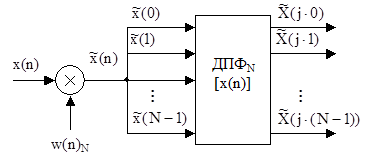 – преобразуемая входная последовательность ДПФ; ωk=k×ωд/N или fk=k×fд/N – частоты анализа, называемые также бинами ДПФ: 1 бин равен шагу дискретизации сигнала в частотной области fд/N. Анализатор имеет N разнесенных по частоте на 1 бин (fд/N) каналов анализа с центральными частотами ωk (fk), при этом значения k=0,1,…N–1 соответствуют номеру канала, номеру бина или номеру частотной выборки ДПФ  . Весовая функция представляет окно, через которое наблюдается входной сигнал, длиной ее определяется время анализа Tа=N×Tд или время наблюдения сигнала. Рис. 4. Структурная схема анализатора спектра на основе ДПФ Умножению или взвешиванию во временной области соответствует свертка в частотной, поэтому вычисляемое ДПФ фактически является дискретизированной сверткой истинного спектра анализируемого сигнала X(j×ω) с частотной характеристикой (спектром) весовой функции W(j×ω):  , где * – символ свертки, т.е. содержит систематическую (методическую) погрешность анализа. Она является следствием ограничения сигнала по длительности, искажающего результаты спектрального анализа. |
,