Лабораторные работы 6.5 - 6.10. Исследование эффекта холла в полупроводниках

• Название: Исследование эффекта холла в полупроводниках
• Дата: 14.03.2022
• Размер: 112.85 Kb.
• Имя файла: Лабораторные работы 6.5 - 6.10.docx
• Тип: Исследование; #395377
• страница: 1 из 4

.

Лабораторная работа № 6.10

ИССЛЕДОВАНИЕ ЭФФЕКТА ХОЛЛА В ПОЛУПРОВОДНИКАХ

ЦЕЛЬ РАБОТЫ

1. 
   Изучить теорию эффекта Холла.
   
2. 
   Исследовать зависимость э.д.с. Холла U_x
   

от величины индукции

внешнего магнитного поляB и силы тока I, протекающего через об- разец.

3. 
   Определить концентрацию основных носителей заряда n
   

движность  .

и их по-

КРАТКАЯ ТЕОРИЯ

Эффектом Холла называют явление возникновения э.д.с. в помещённом в магнитное поле полупроводнике, по которому протекает электрический ток. Пусть полупроводник имеет форму параллелепипеда длиной lи сечением

a bи по нему протекает ток Iперпендикулярно сечен_→ию. Полупроводник

находится в однородном магнитном поле с индукцией B, направление кото- рой перпендикулярно направлению тока и указано на рис.10.1.





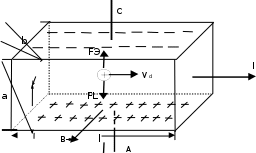
Рисунок 10.1 – Механизм возникновения холловской ЭДС
Опыт показывает, что между точками Aи C,расположенными на нижней и верхней гранях образца, возникает разностьпотенциалов,названнаяэ.д.с.

Холла_→,которая возрастает с увеличением тока Iи вектора магнитной индук-

ции B: ^U_x ^{I B}. Объясняется возникновение U_х смещением движущихся за-

рядов к верхней или нижней грани образца под действием силы Лоренца. Ес- ли основными носителями заряда являются дырки, то силой Лоренца (рис.10.1) они отклоняются к нижней грани образца, и там накопится поло-

жительный заряд, а на верхней останется не скомпенсированный отрицатель- ный заряд. Если основными носителями заряда являются электроны, то они будут также отклоняться и накапливаться на нижней грани, создавая на ней отрицательный заряд. (Вспомните правило левой руки, по которому в данном случае определяем направление силы Лоренца).

Величина силы Лоренца определяется соотношением:


F

d

L
^→  qv^→  B^→, (1)

где q- заряд носителя,

v^→ - его дрейфовая скорость. Смещение носителей

d _{→ →}

заряда в поперечном (по отношению v_dи B) направлении прекратится тогда,

когда сила Лоренца уравновесится силой F_ээлектрического поля, создавае-


d
мого сместившимися зарядами. Если Bv^→ , то:

qv_d  B qE_x. (2)

Дрейфовая скорость может быть выражена из формулы для плотности дрейфового тока:

v_d

jq n

. (3)

Если плотность тока Jодинакова во всех точках сечения a b, то:

j ^Ia b

. (4)

После подстановки уравнений (4) и (3) в формулу (2) получим:

E <sup>1

x</sup> qn

 ^IB. (5)

ab

Считая возникшее поле однородным, найдем холловское напряжение на

контактах АС, используя связь напряженности

U_x:

E_x и разности потенциалов

U_x E_x

a  ¹

qn

 ^IB Rb ^x

 ^IB. (6)

b

Величина R   ¹

называетсяпостояннойХолла.

x _qn

Предложенный вывод выражения для U_x

нагляден, но недостаточно

строг. Не был учтён статистический характер распределения носителей заря- да по скоростям. Это значит, что уравнение (2) не может выполняться одно- временно для всех электронов (или дырок), имеющих различные по величине и направлению скорости. Поэтому стационарное состояние наступает не то- гда, когда сила Лоренца уравновешивает силу электрического поля Холла для каждого электрона, а тогда, когда ток, созданный холловским электриче- ским полем U_x , компенсирует ток, созданный действием силы Лоренца. Од- нако результат строгой теории эффекта Холла для атомарных полупроводни- ков Ge и Si практически не отличается от полученного нами. В нашей лабо- раторной работе используется датчик, Холла изготовленный из кремния.

Итак, измеренное значение напряжения Холла U_xи знание условий экспе- римента (размеры образца, величина тока I, вектор магнитной индукции B^→ )

дают возможность определить знак и концентрацию носителей заряда в по-

лупроводнике. А параллельное измерение удельной электропроводности  :

  q n _n

(7)

того же образца позволяет вычислить и подвижность носителей заряда  :

 ^    Rq n ^x

. (8)

Подвижность электрона _n

и подвижность дырки  _p

численно равна ско-

рости, которую приобретает электрон или дырка, в электрическом поле напряженностью равной единице, т.е.:

  ^Un;

n _E

  ^{Up. (9)}

p _E

Подвижность электрона и дырки является одной из основных характери- стик полупроводника, по которой можно судить о степени “загрязнения” ма- териала неконтролируемыми примесями.

Метод определения концентрации и подвижности носителей заряда по холловской э.д.с. и удельной проводимости является классическим методом научного исследования полупроводников.

ОПИСАНИЕ УСТАНОВКИ

Лабораторная работа выполняется при комнатной температуре с исполь- зованием постоянного тока через образец и магнитного поля электромагнита. Принципиальная схема измерительной установки изображена на рис.10.2.
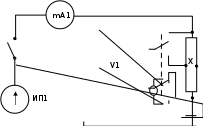
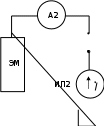
Рисунок 10.2 – Принципиальная схема измерительной установки
ИП 1, ИП 2 – источники питания схемы; mA1 – миллиамперметр для из- мерения силы тока через образец; V1 – вольтметр для измерения холловского напряжения и падения напряжения на образце; X – полупроводниковый об- разец для исследования эффекта Холла; ЭМ – электромагнит; A2 –амперметр для измерения силы тока через электромагнит.

Геометрические размеры образца кремния указан_→ы на стенде. В условиях

нашего эксперимента вектор магнитной индукции Bпрямо пропорционален