Исследование функции с помощью производных Точками экс. Исследование функции с помощью производных. Точками экстремума функции являются точки, в которых функция определена и проходя через которые производная меняет знак. Если в точке x 0
 Скачать 95.43 Kb. Скачать 95.43 Kb.
|
|
19. Задача об оптимальном распределении ресурсов: построение модели Пусть на некотором предприятии изготавливаются n видов продукции из s видов сырья. Известно, что на изготовление одной еденицы продукции j-го вида нужно aij единиц сырья i-го вида. В распоряжении предприятия имеется bi единиц сырья i-го вида. Известно так же, что на каждой единице продукции j-о вида предприятие получает сj единиц прибыли. Требуется определить, сколько единиц х1, х2…хn Каждого вида должно изготовить предприятие, чтобы обеспечить себе максимальную прибыль. Общая задача линейного программирования f(x)=с1х1+ с2х2+…+сnхn ->mах или <-c,x> inf а11х1 + а12х2 +... + а1nхn<=b1, а21х1 + а22х2 +... + а2nхn<=b2, ……………………………… am1х1 + аm2х2 +... + аmnхn<=bm, x1>=0 ,x2>=0, …, xn>=0 где аik, bk, ci - заданные числа. А вот как выглядят запись общей задаче линейного программировании:  xk≥0 ,k=1,2,…,n xk≥0 ,k=1,2,…,n20.Задача об оптимальном распределении ресурсов: графическая интерпретация решения и его устойчивость. Графический метод целесообразно применять для решения задачи линейного программирования, содержащих 2-е переменные, когда ограничения выражены неравенствами. В этом случае ЗЛП имеет вид: 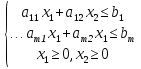 Каждое неравенство ограничений определяет полуплоскость с граничными прямыми 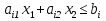 . .В результате построения всех прямых, входящих в систему ограничений, будет получено множество допустимых решений, которое может быть представлено следующими видами:1)Выпуклый многоугольник;2)Выпуклая многоугольная неограниченная область;3)Пустая область;4)Луч;5)Отрезок;6)Единственная точка. Целевая функция определяет на плоскости семейство параллельных прямых, каждый из которых соответствует определенное значение z. Для нахождения оптимального решения графическим способом необходимо знать направление наискорейшего возрастания целевой функции. Это направление показывает вектор градиента целевой функции, который выглядит 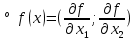 . Тогда ЗЛП можно сформировать так: найти такое значение z, при котором прямя . Тогда ЗЛП можно сформировать так: найти такое значение z, при котором прямя 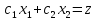 пересекает допустимое множество , причем в этой области пересечения целевая функция должна достигать своего максимального значения. пересекает допустимое множество , причем в этой области пересечения целевая функция должна достигать своего максимального значения.Алгоритм решения ЗЛП графическим методом:1)Построить допустимое множество решений;2)Построить график целевой функции, проходящей через начало координат;3)Построить вектор градиента целевой функции 4)Передвигать график целевой функции в направлении вектора градиента до тех пор, пока он не коснется крайней (угловой) точки множества решений и буде оптимальным решением. Теорема: Если ЗЛП имеет оптимальное решение, то целевая функция принимает оптимальное значение в одной из угловых точек множества допустимых решений ( или многогранника решений). Если линейная (целевая) функция принимает оптимальное значение более чем в одной угловой точке, то она принимает его в любой точке отрезка, соединяющего эти угловой точки. 21. Предмет, цель и задачи теории прогнозирования. Основные методы статистического прогнозирования. Прогноз-это научно-обоснованное суждение, о возможных состояниях объекта в будущем или об альтернативных путях и сроках их достижения. Прогнозирование-процесс разработки прогноза. МОТП-раздел математики, занимающийся разработкой и применением статистических методов для измерения взаимосвязи между различными переменными и построение на их основе научно-обоснованных суждений. Объектом МОТП являются все системы и сферы жизнедеятельности человека, где необходимы прогнозы. Предметом МОТП является количественная оценка взаимосвязи между случайными событиями, признаками, показателями также проверка теоретических моделей реальных процессов для получения прогнозов. Целью МОТП является оценка точечных и интервальных прогнозов деятельности генеральной совокупности объектов системы на основании расчетов по данным выборочной совокупности или реализации случайных процессов. Основными методами являются: парная линейная регрессия, парная нелинейная регрессия, множественная регрессия, временной анализ рядов, системы одновременных уравнений. Модель парной регрессииy=f(x)+E Линейная Нелинейная Степенная Экспоненциальная Парная регрессия применяется, когда можно выделить мощный фактор х, который сильно влияет на изменение у. Модель множественной регрессии Линейная Нелинейная Применяется для долгосрочных и среднесрочных прогнозов. Когда на у влияют сильно несколько факторов. Анализ временных рядов Временной ряд-значение показателя за время. Аддитивная модель y=T+S+C+E Мультипликативная модель y=T*S*C*E T-трендовая часть, S-сезонность, C-цикличность компонента, E-случайное отклонение. Системы одновременных уравнений Независимые Системы взаимосвязанных уравнений Рекурсивные уравнения 22. Метод наименьших квадратов (МНК) в оценке параметров модели прогнозирования, его графическая интерпретация. Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b  т.е. при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. Необходимое условие: производная F равна нулю. т.е. при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. Необходимое условие: производная F равна нулю. 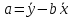 ; ;  Составим определитель: Составим определитель: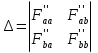 , если , если 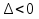 экстремумов нет. Если экстремумов нет. Если  есть экстремумы. Если есть экстремумы. Если  необходимы дополнительные исследования. Если необходимы дополнительные исследования. Если  – точка максимума. Если – точка максимума. Если 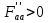 – точка минимума. Замечания: 1)Уравнение прямой линии a+bx проходит через точки ( – точка минимума. Замечания: 1)Уравнение прямой линии a+bx проходит через точки ( ) 2)Дисперсия не равна нулю. Графическая интерпретация МНК: Из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной. 23. Оценка качества модели прогнозирования. Коэффициент детерминации. Качество модели прогнозирования проверяется с помощью коэффициента детерминации. 1) ) 2)Дисперсия не равна нулю. Графическая интерпретация МНК: Из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной. 23. Оценка качества модели прогнозирования. Коэффициент детерминации. Качество модели прогнозирования проверяется с помощью коэффициента детерминации. 1) – общая сумма квадратов отклонений изучаемого показателя от его среднего значения. 2) – общая сумма квадратов отклонений изучаемого показателя от его среднего значения. 2)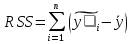 – сумма квадратов отклонений, объясняемая регрессией. 3) – сумма квадратов отклонений, объясняемая регрессией. 3)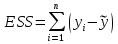 – остаточная сумма отклонений, объясняемая другими факторами. Общее соотношение: TSS=RSS+ESS R2= – остаточная сумма отклонений, объясняемая другими факторами. Общее соотношение: TSS=RSS+ESS R2=  , R2 = [0,1] Если R21, значит доля объясняемой дисперсии велика, тогда ESS0. , R2 = [0,1] Если R21, значит доля объясняемой дисперсии велика, тогда ESS0.Если R2 0, тогда фактор Х слабо объясняет изменения. Если RSS гораздо больше, чем ESS, то уравнение регрессии статистически значимо. Сумма квадратов отклонений имеет определенное число степеней свободы связано с числом наблюдений показателя у (количество точек) и числом определенных по ним констант. Чтобы проверить качество выдвигаются гипотезы: Н0 – уравнение не значимо; Н1 – уравнение значимо, проверяется при помощи критерия Фишера. Fнабл=  (n-2), Fкр=F(;m;n-m-1), m-количество переменных, n-количество точек. Vкр=(Fкр;+∞), если Fнабл>Fкр, то принимается Н1 24.Факторные модели в экономических исследованиях. В факторных моделях предполагается, что доходность ценной бумаги реагирует на изменение различных факторов (индексов)Для попыток точно оценить ожидаемость доходности, дисперсии, ковариации ценных бумаг используют так называемые многофакторные модели. Это объясняется тем, что фактические доходности по ценным бумагам по ценным бумагам оказываются чувствительными к изменению индекса рынка, к уровню процентных ставок, инфляции, темпам прироста ВВП и т.д. В случае k факторов (F1,F2, …, Fk) каждая ценная бумага будет обладать чувствительностями (b1, b2, …, bk) в следующей k-факторной модели. (n-2), Fкр=F(;m;n-m-1), m-количество переменных, n-количество точек. Vкр=(Fкр;+∞), если Fнабл>Fкр, то принимается Н1 24.Факторные модели в экономических исследованиях. В факторных моделях предполагается, что доходность ценной бумаги реагирует на изменение различных факторов (индексов)Для попыток точно оценить ожидаемость доходности, дисперсии, ковариации ценных бумаг используют так называемые многофакторные модели. Это объясняется тем, что фактические доходности по ценным бумагам по ценным бумагам оказываются чувствительными к изменению индекса рынка, к уровню процентных ставок, инфляции, темпам прироста ВВП и т.д. В случае k факторов (F1,F2, …, Fk) каждая ценная бумага будет обладать чувствительностями (b1, b2, …, bk) в следующей k-факторной модели. 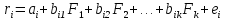 , где ai – ожидаемая доходность ценной бумаги i при условии, что каждый фактор имеет нулевое значение. ξ – случайная ошибка с нулевым математическим ожиданием и некоррелированная с факторами (F1,F2, …, Fk). Причем разным ценным бумагам соответствуют различные случайные ошибки, имеющие нулевую совместную ковариацию. Примером однофакторной модели может служить рыночная модель. Здесь , где ai – ожидаемая доходность ценной бумаги i при условии, что каждый фактор имеет нулевое значение. ξ – случайная ошибка с нулевым математическим ожиданием и некоррелированная с факторами (F1,F2, …, Fk). Причем разным ценным бумагам соответствуют различные случайные ошибки, имеющие нулевую совместную ковариацию. Примером однофакторной модели может служить рыночная модель. Здесь 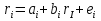 , (1) где ri - доходность ценной бумаги i за данный период, rI - доходность на рыночный индекс I за этот же период, случайная величина. ai, bi - коэффициенты смещения, или нулевой фактор, и коэффициент наклона, или чувствительность к фактору, соответственно. ξi – случайная погрешность. Случайная погрешность показывает, что факторная модель не очень точно объясняет доходности ценных бумаг. На практике все инвесторы явно или неявно применяют факторные модели, потому что невозможно рассматривать взаимосвязь каждой ценной бумаги, с другой в отдельности. Согласно однофакторной модели (1) ожидаемая доходность ценной бумаги может быть записана в виде , (1) где ri - доходность ценной бумаги i за данный период, rI - доходность на рыночный индекс I за этот же период, случайная величина. ai, bi - коэффициенты смещения, или нулевой фактор, и коэффициент наклона, или чувствительность к фактору, соответственно. ξi – случайная погрешность. Случайная погрешность показывает, что факторная модель не очень точно объясняет доходности ценных бумаг. На практике все инвесторы явно или неявно применяют факторные модели, потому что невозможно рассматривать взаимосвязь каждой ценной бумаги, с другой в отдельности. Согласно однофакторной модели (1) ожидаемая доходность ценной бумаги может быть записана в виде  ,(2) где ,(2) где 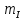 -ожидаемое значение фактора. Дисперсия ценной бумаги равняется -ожидаемое значение фактора. Дисперсия ценной бумаги равняется  - дисперсия фактора, - дисперсия фактора,  - дисперсия случайной ошибки. Первое слагаемое в формуле (2) называется факторным риском, а второе – нефакторным риском. Ковариация любых двух ценных бумаг - дисперсия случайной ошибки. Первое слагаемое в формуле (2) называется факторным риском, а второе – нефакторным риском. Ковариация любых двух ценных бумаг  учитывая, что ri, ξi, ξj – независимые, т.е. учитывая, что ri, ξi, ξj – независимые, т.е. 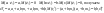 25.Текущая стоимость ценных бумаг с фиксированным доходом. К ценным бумагам с фиксированным доходом относятся: облигации, привилегированные акции, векселя. Рассмотрим безрисковые ценные бумаги на примере облигаций. Рассмотрим облигацию с номиналом N, купонной процентной ставкой С, сроком до погашения n. Будем считать, что среднерыночный безрисковый процент равен i. Текущей стоимостью облигации называется современное значение потока платежей, генерируемого данной облигацией:  где где  - дисконтирующий множитель. Текущая стоимость в случае нулевых купонов, когда обладатель облигации не получает процентный платеж, определяется: - дисконтирующий множитель. Текущая стоимость в случае нулевых купонов, когда обладатель облигации не получает процентный платеж, определяется: 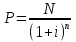 В случае, когда проценты начисляются за весь срок и выплачиваются одной суммой вместе с номиналом, текущая стоимость определяется по формуле: В случае, когда проценты начисляются за весь срок и выплачиваются одной суммой вместе с номиналом, текущая стоимость определяется по формуле:  Полной доходностью будем называть решение предыдущих уравнений относительно процентной ставки i, если вместо текущей стоимости в уравнении поставить рыночную стоимость. Полной доходностью будем называть решение предыдущих уравнений относительно процентной ставки i, если вместо текущей стоимости в уравнении поставить рыночную стоимость.26.Применение теории вероятностей в финансовом анализе. Применительно к задачам финансовой математики модель теории вероятностей предполагает, что, в частности , будущая стоимость ценной бумаги S1=S(ω) является случайной величиной, т.е. функции элементарных исходов ω. Тогда доходность  . Также является случайной величиной, как функция от случайной величины. Изменчивость доходности ценной бумаги может быть охарактеризована величиной дисперсии доходности . Также является случайной величиной, как функция от случайной величины. Изменчивость доходности ценной бумаги может быть охарактеризована величиной дисперсии доходности  , где ρ – случайная доходность. , где ρ – случайная доходность.  - математическое ожидание или среднее значение доходности. Интуитивно риск инвестиции представляет собой нечто вроде вероятности нежелательного события, когда цена или доходность некоторой ценной бумаги сильно отклоняется от прогнозируемого значения. Эта вероятность может быть оценена через среднее квадратическое отклонение σ. - математическое ожидание или среднее значение доходности. Интуитивно риск инвестиции представляет собой нечто вроде вероятности нежелательного события, когда цена или доходность некоторой ценной бумаги сильно отклоняется от прогнозируемого значения. Эта вероятность может быть оценена через среднее квадратическое отклонение σ. 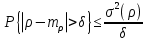 . Это неравенство известно, как неравенство Чебышева. Оно позволяет оценить сверху вероятность неблагоприятных событий. Видно, что оценка вероятности больших отклонений от среднего значения пропорциональна дисперсии. В силу этого в финансовой математике в качестве меры риска часто принимают дисперсию σ2 или среднеквадратическое отклонение σ. . Это неравенство известно, как неравенство Чебышева. Оно позволяет оценить сверху вероятность неблагоприятных событий. Видно, что оценка вероятности больших отклонений от среднего значения пропорциональна дисперсии. В силу этого в финансовой математике в качестве меры риска часто принимают дисперсию σ2 или среднеквадратическое отклонение σ. |
