Исследование функции с помощью производных Точками экс. Исследование функции с помощью производных. Точками экстремума функции являются точки, в которых функция определена и проходя через которые производная меняет знак. Если в точке x 0
 Скачать 95.43 Kb. Скачать 95.43 Kb.
|
|
1.Исследование функции с помощью производных. Точками экстремума функции являются точки, в которых функция определена и проходя через которые производная меняет знак. Если в точкеx0 есть экстремум, то f'(x0) = 0 либо значения f'(x0) не существует. – если вторая производная f‘’(x) < 0 на интервале, то график функции f(x) является выпуклым на данном интервале; – если вторая производная f ‘’(x) > 0 на интервале, то график функции f(x) является вогнутым на данном интервале. Если в точкеx0 есть перегиб графика функцииy=f(x), то:f ‘’(x0) = 0 либо значенияf ‘’(x0) не существует. Если вторая производнаяy=f ‘’ (x) при переходе через точкуx0 меняет знак, то в данной точке существует перегиб графика функции y=f(x) . Асимптота – это прямая, к которой неограниченно близко приближается график функции при удалении его переменной точки в бесконечность. чтобы установить наличие вертикальной асимптотыx=αв точкеx=αдостаточно показать, что хотя бы один из односторонних пределов 2. Понятие о неопределенном и определенном интеграле. Интегрирование заменой переменных. Вычислить неопределённый интеграл означает восстановить функцию по известной производной этой функции. Восстановленная таким образом функция F(x) называется первообразной для функции f(x). Неопределённым интегралом функции f(x) называется совокупность всех её первообразных. При этом употребляется запись ∫f(x)dx, где знак ∫ называется знаком интеграла, функция f(x) – подынтегральной функцией, а f(x)dx – подынтегральным выражением. Таким образом, если F(x) – какая-нибудь первообразная для f(x) , то ∫f(x)dx=F(x)+C. Замена переменной. Пусть функция x=φ(t) определена и дифференцируема на некотором промежутке Ти пусть Х– множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Хфункция f(x) имеет первообразную, то на множестве Т справедлива формула ∫f(x)dx=∫f[φ(t)]φ’(t)dt (1) Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где a не= b) называется приращение какой-нибудь её первообразной на этом отрезке. При этом употребляется запись 3.Способы представления решения СЛАУ: метод Гаусса, правило Крамера, матричный способ. 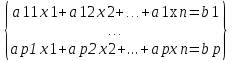 x1,x2,..,xn-неизвестные переменные ,аig,i=1,..p,g=1,n-коэффициенты,b1,b2,..bn-свободные члены. Такую форму записи СЛАУ называют координатой. Решением СЛАУ называют набор значений неизвестных переменных х1= α1,х2=α2,..,хn=αn,обращающий все уравнения системы в тождества.Матричное уравнение А*Х=В при данных значениях неизвестных переменных так же обращается в тождество А*Х=В.Если система уравнений имеет хотя бы одно решение,то она называется совместной.Если система не имеет решений, то она несовместна. Если СЛАУ имеет единственное решение, то ее называют определенной, если решений больше,тонеопределенной.Если свободные члены всех уравнений системы равны нулю b1=b2=..=bn=0, то система называетсяоднородной,в противном случае неоднородной.Если число уравнений системы равно числу неизвестных переменных и определить ее основной матрицы не равен нулю,то такие СЛАУ называется элементарными. Решение СЛАУ методом Крамера.Пусть нам требуется решить СЛАУ x1,x2,..,xn-неизвестные переменные ,аig,i=1,..p,g=1,n-коэффициенты,b1,b2,..bn-свободные члены. Такую форму записи СЛАУ называют координатой. Решением СЛАУ называют набор значений неизвестных переменных х1= α1,х2=α2,..,хn=αn,обращающий все уравнения системы в тождества.Матричное уравнение А*Х=В при данных значениях неизвестных переменных так же обращается в тождество А*Х=В.Если система уравнений имеет хотя бы одно решение,то она называется совместной.Если система не имеет решений, то она несовместна. Если СЛАУ имеет единственное решение, то ее называют определенной, если решений больше,тонеопределенной.Если свободные члены всех уравнений системы равны нулю b1=b2=..=bn=0, то система называетсяоднородной,в противном случае неоднородной.Если число уравнений системы равно числу неизвестных переменных и определить ее основной матрицы не равен нулю,то такие СЛАУ называется элементарными. Решение СЛАУ методом Крамера.Пусть нам требуется решить СЛАУ  Пусть Пусть 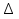 -определитель основной матрицы системы. -определитель основной матрицы системы.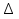 x1, x1, -определитель матриц,которые получаются из А заменой 1го,2го и т.д. столбцов соответственно на столбец свободных членов.Неизвестные переменные вычисляются по формулам метода Крамера,как -определитель матриц,которые получаются из А заменой 1го,2го и т.д. столбцов соответственно на столбец свободных членов.Неизвестные переменные вычисляются по формулам метода Крамера,как , , ..так находится решение СЛАУ. Решение СЛАУ матричным методом.Пусть СЛАУ задана в матричном виде А*Х=В,где А с размерностью n*n и ..так находится решение СЛАУ. Решение СЛАУ матричным методом.Пусть СЛАУ задана в матричном виде А*Х=В,где А с размерностью n*n и  ,т.к. ,т.к.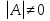 ,то матрица А-обратима,т.е.существует обратная матрица А-1 .Если обе части уравнения А*Х=В умножить на А-1 ,то А-1*А*Х= А-1 *В ,то матрица А-обратима,т.е.существует обратная матрица А-1 .Если обе части уравнения А*Х=В умножить на А-1 ,то А-1*А*Х= А-1 *В 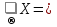 А-1 *В . Решение СЛАУ методом Гаусса. Рассм.систему А-1 *В . Решение СЛАУ методом Гаусса. Рассм.систему 1 шаг-прямой ход метода Гаусса составляем расширенную матрицу 1 шаг-прямой ход метода Гаусса составляем расширенную матрицу 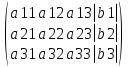 C помощью элементарных преобразований приводим матрицу к ступенчатому виду: C помощью элементарных преобразований приводим матрицу к ступенчатому виду: 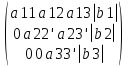 2шаг-обратный ход метода Гаусса по ступенчатой матрице выписываем систему, откуда находим x1,x2,x3. 2шаг-обратный ход метода Гаусса по ступенчатой матрице выписываем систему, откуда находим x1,x2,x3.  X3 X3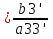 ; X2 ; X2 ; X1 ; X1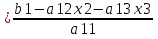 4.Определитель матрицы. Его свойства и правила вычисления. Определителем n-го порядка называется число, которое вычисляется по теореме Лапласса: любой определитель равен сумме произведений элементов любой строки или столбца на их алгебраическое дополнение:  . Алгебраическим дополнением элемента aij матрицы А называется число - . Алгебраическим дополнением элемента aij матрицы А называется число -  где где  определитель матрицы получающийся из исходной матрицы А путем вычеркивания i–ой строки и j–го столбца.Свойства определителя: 1.Определитель не меняется при транспонировании; 2.Если какая-то строка определителя состоит из нулей, то такой определитель равен нулю. Аналогично для столбца. 3.При перестановке двух строк определителя, он меняет знак. 4.Определитель содержащий две одинаковые строки равен нулю. 5.Если элементы некоторой строки умножить на некоторое число, то сам определитель умножается на это число 6.Определитель содержащий две пропорциональные строки равен нулю. 7.Определитель порядка n можно представить в виде суммы двух определителей. 8.Если одна из строк определителя есть линейная комбинация его других строк, то такой определитель равен нулю. 9.Определитель не меняется, если к элементам одной из строк прибавляются соответствующие элементы других строк, умноженных на одно и тоже число. Правила вычисления определителей: 1.Для определителей 1,2,3 порядков есть специальные формулы, указанные выше. 2.Для определителя порядка n применяется теорема Лапласса. 3.Занулить элементы, стоящие под главной диагональю и перемножить элементы, стоящие на главной диагонали. 5.Собственные вектора и собственные значения матрицы. Пусть дана матрица А Собственным вектором матрицы А называется ненулевой вектор, для которого выполняется равенство АХ=λХ, а число λ называется собственным значением. Для нахождения λ составляют характеристическое уравнение определитель матрицы получающийся из исходной матрицы А путем вычеркивания i–ой строки и j–го столбца.Свойства определителя: 1.Определитель не меняется при транспонировании; 2.Если какая-то строка определителя состоит из нулей, то такой определитель равен нулю. Аналогично для столбца. 3.При перестановке двух строк определителя, он меняет знак. 4.Определитель содержащий две одинаковые строки равен нулю. 5.Если элементы некоторой строки умножить на некоторое число, то сам определитель умножается на это число 6.Определитель содержащий две пропорциональные строки равен нулю. 7.Определитель порядка n можно представить в виде суммы двух определителей. 8.Если одна из строк определителя есть линейная комбинация его других строк, то такой определитель равен нулю. 9.Определитель не меняется, если к элементам одной из строк прибавляются соответствующие элементы других строк, умноженных на одно и тоже число. Правила вычисления определителей: 1.Для определителей 1,2,3 порядков есть специальные формулы, указанные выше. 2.Для определителя порядка n применяется теорема Лапласса. 3.Занулить элементы, стоящие под главной диагональю и перемножить элементы, стоящие на главной диагонали. 5.Собственные вектора и собственные значения матрицы. Пусть дана матрица А Собственным вектором матрицы А называется ненулевой вектор, для которого выполняется равенство АХ=λХ, а число λ называется собственным значением. Для нахождения λ составляют характеристическое уравнение  АХ=λХ Получили систему линейных однородных уравнений. СЛОУ будет иметь ненулевое решение, если определитель системы равен нулю, т.е. АХ=λХ Получили систему линейных однородных уравнений. СЛОУ будет иметь ненулевое решение, если определитель системы равен нулю, т.е.  6.Алгоритм решения линейного неоднородного дифференциального уравнения первого порядка. Задача Коши. Линейным дифференциальным уравнением 1-го порядка называется уравнение  потому что у и у’ входят в него линейно. потому что у и у’ входят в него линейно.  (ЛОДУ) (ЛОДУ)  (ЛНДУ). Для того, чтобы проинтегрировать ЛНДУ 1-го порядка, необходимо проинтегрировать соответствующее ему ЛОДУ 1-го порядка (т.е. решив промежуточную задачу, записав ноль в правой части), а затем применить метод Лагранжа. Интегрирование ЛОДУ Всякое ЛОДУ 1-го порядка интегрируется разделением переменных: (ЛНДУ). Для того, чтобы проинтегрировать ЛНДУ 1-го порядка, необходимо проинтегрировать соответствующее ему ЛОДУ 1-го порядка (т.е. решив промежуточную задачу, записав ноль в правой части), а затем применить метод Лагранжа. Интегрирование ЛОДУ Всякое ЛОДУ 1-го порядка интегрируется разделением переменных: Метод Лагранжа (метод вариации постоянной) В формуле (2) считать, что С является неизвестной функцией. Варьируем постоянную Найдем такую функцию С(х), чтобы формула (2) являлась решением ЛНДУ (1). Подставляем Закон является всеобщим и действует для всех ЛНДУ любого порядка Задача Коши.Для того, чтобы из бесконечного числа решений выделить одно, необходимо дополнительное условие. Для ДУ 1-го порядка в нормальной форме: Таким дополнительным условием является условие Коши y(x0)=y0 – условие Коши. А такая задача называется задачей Коши: y'=f(x,y), y(x0)=y0, где x0, y0 – любые числа, начальные условия функции. 7.Алгоритм решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами. Задача Коши.Пусть дано ДУ:  *. Для каждого такого уравнения можно записать соответствующее однородное уравнение: *. Для каждого такого уравнения можно записать соответствующее однородное уравнение: 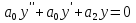 . Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения. . Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения.  . Найдем . Найдем 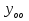 . Рассмотрим лоду. Составляем характеристическое уравнение . Рассмотрим лоду. Составляем характеристическое уравнение 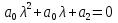 . Пусть λ1,λ2 корни уравнения, причем среди них могут быть и кратные. Возможны следующие случаи: а) λ1,λ2 - вещественные и различные Тогда ФСР уравнения (1) имеет вид . Пусть λ1,λ2 корни уравнения, причем среди них могут быть и кратные. Возможны следующие случаи: а) λ1,λ2 - вещественные и различные Тогда ФСР уравнения (1) имеет вид  и общим решением однородного уравнения будет и общим решением однородного уравнения будет  . б) λ1,λ2 - вещественные и кратные. ФСР . б) λ1,λ2 - вещественные и кратные. ФСР  , общее решение , общее решение . в) λ1,λ2 – комплексные. . в) λ1,λ2 – комплексные.   . ФСР . ФСР  , ,  . Общее решение . Общее решение  2) Найдем 2) Найдем  а) метод подбора. Общий вид правой части f(x) уравнения (*), при котором возможно применить метод подбора, следующий: а) метод подбора. Общий вид правой части f(x) уравнения (*), при котором возможно применить метод подбора, следующий:   - многочлены степени e и m соответственно. В этом случае частное решение уравнения (*) ищется в виде - многочлены степени e и m соответственно. В этом случае частное решение уравнения (*) ищется в виде  ] где ] где  , ,   многочлены от х к-ой степени общего вида с неопределенными коэффициентами, а S – кратность корня характеристического уравнения. б) принцип суперпозиции/ При нахождении частных решений ЛНДУ удобно пользоваться принципом суперпозиции. Теорема. Если yk(x) ест решение уравнения многочлены от х к-ой степени общего вида с неопределенными коэффициентами, а S – кратность корня характеристического уравнения. б) принцип суперпозиции/ При нахождении частных решений ЛНДУ удобно пользоваться принципом суперпозиции. Теорема. Если yk(x) ест решение уравнения  , k=1,2. То функция , k=1,2. То функция  является решением уравнения является решением уравнения  . в) задача Коши. Как известно з.К. для ЛНУ . в) задача Коши. Как известно з.К. для ЛНУ 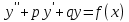 , состоит: в нахождении решения этого уравнения, удовлетворяющего начальным условиям: , состоит: в нахождении решения этого уравнения, удовлетворяющего начальным условиям: 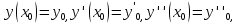 8. Классическое определение вероятности. Основные формулы комбинаторики. Геометрическое определение вероятности. Вероятностью события называется численная мера объективной возможности наступления этого события. Два события называются совместными, если наступление одного из них не исключает возможность наступление другого. События А1, А2,…,Аnявляются исходами одного испытания называются равновозможными, если в результате испытания по условиям симметрии ни одно из этих событий не являются объективно более возможным. Вероятность события, эксперимент по воспроизведению, которого можно разложить на равновозможные исходы, равна отношению числа исходов, благоприятствующих этому событию к общему числу исходов, т.е. P(A)=m/n, m-общее число исходов, n-число исходов, благоприятствующих событию. Сочетаниями Сnm называется соединение, состоящее из m элементов и отличающиеся друг от друга состоянием элементов. Число сочетаний из n по m равно числу способов выбора m элементов из n. Cnm=n!/m!(n-m)!. РазмещениямиAnm называется соединение, состоящее из m элементов и отличающиеся друг от друга либо составом элементов, либо порядок их следования. Anm=n!/(n-m)!. Перестановками Рn называется соединение, состоящее из n элементов и отличающееся друг от друга порядком следования элементов. Рn=n!.Если в сочетании некоторые элементы могут повторятся, то их называют сочетания с повторениями. 8. Классическое определение вероятности. Основные формулы комбинаторики. Геометрическое определение вероятности. Вероятностью события называется численная мера объективной возможности наступления этого события. Два события называются совместными, если наступление одного из них не исключает возможность наступление другого. События А1, А2,…,Аnявляются исходами одного испытания называются равновозможными, если в результате испытания по условиям симметрии ни одно из этих событий не являются объективно более возможным. Вероятность события, эксперимент по воспроизведению, которого можно разложить на равновозможные исходы, равна отношению числа исходов, благоприятствующих этому событию к общему числу исходов, т.е. P(A)=m/n, m-общее число исходов, n-число исходов, благоприятствующих событию. Сочетаниями Сnm называется соединение, состоящее из m элементов и отличающиеся друг от друга состоянием элементов. Число сочетаний из n по m равно числу способов выбора m элементов из n. Cnm=n!/m!(n-m)!. РазмещениямиAnm называется соединение, состоящее из m элементов и отличающиеся друг от друга либо составом элементов, либо порядок их следования. Anm=n!/(n-m)!. Перестановками Рn называется соединение, состоящее из n элементов и отличающееся друг от друга порядком следования элементов. Рn=n!.Если в сочетании некоторые элементы могут повторятся, то их называют сочетания с повторениями.  nm=Cn+m-1m. Если в размещениях элементы могут повторяться, их называют размещения с повторениями. Аnm=nm. Геометрическое определение вероятностей. Если эксперимент по воспроизведению некоторого события можно разложить на бесконечное число равновозможных исходов, то вероятности таких событий определяется по геометрической схеме. Вероятность события Р(А)=m(G)/n(S), m(G)-мера благоприятствующее событию А; n(S)-мера всей области. В качестве меры области может выступать длина отрезка, площадь фигуры, объем тела. Требования к применению геометрической схемы определения вероятности: 1) исходные области должны быть замкнуты; 2) области должны быть измеримы. nm=Cn+m-1m. Если в размещениях элементы могут повторяться, их называют размещения с повторениями. Аnm=nm. Геометрическое определение вероятностей. Если эксперимент по воспроизведению некоторого события можно разложить на бесконечное число равновозможных исходов, то вероятности таких событий определяется по геометрической схеме. Вероятность события Р(А)=m(G)/n(S), m(G)-мера благоприятствующее событию А; n(S)-мера всей области. В качестве меры области может выступать длина отрезка, площадь фигуры, объем тела. Требования к применению геометрической схемы определения вероятности: 1) исходные области должны быть замкнуты; 2) области должны быть измеримы.9. Простые и сложные события. Основные теоремы теории вероятностей: теорема сложения, теорема умножения. Событием называется всякий факт, который может произойти или не произойти при выполнении определенного комплекса условий. Сложным называется событие, если его нельзя разложить на более простые. Суммой 2-х событий А и В называется событие С, которое состоит в наступлении либо события А, либо – В: С=А+В. Произведением 2-х событий А и В называется событие С, состоящее в наступлении событий А и В одновременно. Под отрицанием события А понимают наступление противоположному к нему события. Свойства: 1)А+В=В+А 2)А+(В+С)=(А+В)+С 3)А*В=В*А 4) А*(В*С)=(А*В)*С 5)(А+В)*С=А*С+В*С 1.А+А=Ω 2.А*А=А 3.А*А=0 4.А+0=А 5.А*0=0 Теорема сложения: вероятность суммы 2-х событий равна сумме вероятностей этих событий без вероятности их совместного наступления. Р(А+В)=Р(А)+Р(В)-Р(А*В) Теорема сложения (для не совместных событий): вероятность суммы несовместных событий равна сумме вероятностей этих событий. Следствие 1: сумма вероятностей событий, образующих полную группу, равна 1. Следствие 2. Сумма вероятностей противоположных событий равна 1. 2 события наз-ся зависимыми, если вероятность наступления одного из них зависит от наступления другого события. 2 события наз-ся независимыми, если вероятность наступления одного из них не зависит от наступления другого события. Под условной вероятностью события А понимают вероятность этого события, вычисленную при условии, что другое событие состоялось Р(А/В) или РВ(А). Теорема умножения (для зависимых событий): вероятность произведения 2-х событий равна произведению вероятности одного из них на условную вероятность другого. Р(А*В)=Р(А)* Р(В/А)= Р(В)*Р(А/В) Теорема умножения (для независимых событий): вероятность произведения 2-х независимых событий событий равна произведению вероятностей этих событий. |
