Исследование функции с помощью производных Точками экс. Исследование функции с помощью производных. Точками экстремума функции являются точки, в которых функция определена и проходя через которые производная меняет знак. Если в точке x 0
 Скачать 95.43 Kb. Скачать 95.43 Kb.
|
|
10.Формула полной вероятности. Формула Байеса. Рассмотрим события Н1,Н2,..Нn образующие полную группу событий(гипотезы).Некоторое событие А можно наступить совместно с одним из событий Н1,Н2,..Нn,тогда А=А*Н1+А*Н2+..+А*Нn, т.к. Н1,Н2,..Нn попарно несовместные события,то Р(А)=Р(А*Н1)+Р(А*Н2)+..+Р(А*Нn)=P(Н1)*Р(А/H1)+P(H2)*P(A/H2)+..+P(Hn)*P(A/Hn)=∑P(Hi)*P(A/Hi) P(A)=∑P(Hi)*P(A/Hi) – ф-ла полной вероятности ,в правой части выделим i-оеслагаемой,т.е. P(Hi/A)= 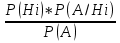 -ф-ла Бейеса. По формуле Бейеса осуществляется переоценка вероятности гипотез при наступившем событии А. 11. Статистические гипотеза и общая схем ее проверки. Виды критической области. Ошибки 1 и 2 рода. Статистической гипотезой называется любое предположение относительно параметров генеральной совокупности и ее законов распределения. Статистическая гипотеза называется параметрической, если в ней сформулировано предположение относительно значения параметров распределения при условии, что задан ЗР. Статистическая гипотеза называется параметрической, если в ней сформулированы предположения относительно вида ЗР генеральной совокупности. Существуют основная (нулевая Н0) и конкурирующая (альтернативная Н1) гипотезы. Статистическая гипотеза называется основной, если она утверждает, что различие между сравнительными параметрами отсутствует, а имеющиеся различия объясняются случайными колебаниями выборки. Конкурирующей называется гипотеза по смыслу противоречивающая основной H0: M(x)=M(y), H1: [M(x)M(y), M(x)>M(y), M(x) -ф-ла Бейеса. По формуле Бейеса осуществляется переоценка вероятности гипотез при наступившем событии А. 11. Статистические гипотеза и общая схем ее проверки. Виды критической области. Ошибки 1 и 2 рода. Статистической гипотезой называется любое предположение относительно параметров генеральной совокупности и ее законов распределения. Статистическая гипотеза называется параметрической, если в ней сформулировано предположение относительно значения параметров распределения при условии, что задан ЗР. Статистическая гипотеза называется параметрической, если в ней сформулированы предположения относительно вида ЗР генеральной совокупности. Существуют основная (нулевая Н0) и конкурирующая (альтернативная Н1) гипотезы. Статистическая гипотеза называется основной, если она утверждает, что различие между сравнительными параметрами отсутствует, а имеющиеся различия объясняются случайными колебаниями выборки. Конкурирующей называется гипотеза по смыслу противоречивающая основной H0: M(x)=M(y), H1: [M(x)M(y), M(x)>M(y), M(x)По способу получения результата:1)процедурные; 2)непроцедурные. Машинно-зависимые языки, в зависимости от их близости к машинным языкам, делятся на три группы: 1) Машинные языки (языки нулевого уровня) 2) Ассемблер языки (языки первого уровня или языки типа 1:1, послед нее означает, что одна ассемблерная команда после транс ляции порождает ровно одну машинную команду); 3) Макроассемблеры (языки второго уровня или языки типа 1:n). Аналогично, машинно-независимые языки включают следующие группы языков (одна из классификаций): 1) Процедурные языки (третий уровень): Си, С++, Паскаль, ФОРТРАН, БЭЙ СИК и др. Процедурные языки требуют детальной разработки алго ритма решения и, по существу, являются языками для записи алгоритмов реше ния задач. 2) Проблемные языки (четвертый уровень) или языки типа "заполни бланк". Это языки описания задач, специализированные языки. Используя подобный язык программирования, пользователь со общает только, какую задачу надо ре шить и с какими данными. 3) Универсальные языки (пятый уровень): ПЛ/1, АЛГОЛ-68, Ада и др. 4) Скриптовые языки -языки программирования, разработанные для записи «сценариев», последовательностей операций, которые пользователь может вы полнять на компьютере. 13. Понятие алгоритма, его свойства и формулы представления. Алгоритм - заранее заданное понятное и точное предписание возможному исполнителю совершить определенную последовательность действий для получения решения задачи за конечное число шагов. Это — не определение в математическом смысле слова, а, скорее, описание интуитивного понятия алгоритма, раскрывающее его сущность. Алгоритм-это точное предписание, определяющее вычис лительный процесс, ведущий от варьируемых исходных данных к искомому результату. Качество алгоритма определяется его свойствами (характе ристиками).К основным свойствам алгоритма относятся следу ющие:1)Понятность для исполнителя. Исполнитель алгоритма должен понимать, как его выполнять. Иными словами, имея алгоритм и произвольный вариант исходных данных, исполнитель должен знать, как надо действовать для выполнения этого алгоритма 2)Массовость. Предполагается, что алгоритм может быть пригоден для решения всех задач данного типа. Например, алго ритм для решения системы линейных алгебраических уравнений должен быть применим к системе, состоящей из произвольного числа уравнений.3)Результативность. (и/или конечность) (Это свойство означает, что алгоритм должен приводить к получению результата за конечное число шагов) состоит в том, что за конечное число шагов алгоритм либо должен приводить к решению задачи, либо после конечного числа шагов останавливаться из-за невозможности получить решение с выдачей соответствующего сообщения, либо неограниченно продолжаться в течение времени, отведенного для исполнения алгоритма, с выдачей промежуточных результатов.4)Определенность (детерминированность). Предписания, входящие в алгоритм, дол жны быть четкими и однозначными. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.5) Дискретность (прерывность). Описываемый алгоритмом процесс и сам алгоритм могут быть разбиты на отдельные элементарные эта пы, возможность выполнения которых на ЭВМ у пользователя не вызывает сомнений. Утверждения и вопросы могут быть использованы в алгоритмах только как подчиненные пред ложения в составе предписания.6)Эффективность. Количество шагов и сами шаги алгоритма должны быть такими, чтобы решение могло быть найдено за конечное и, более того, приемлемое время.Исполнитель алгоритма — это некоторая абстрактная или реальная (техническая, биологическая или биотехническая) система, способная выполнить действия, предписываемые алгоритмом. 14. Общие принципы разработки программного обеспечения. Программы различаются по назначению, выполняемым функциям, формам реализации. Однако можно полагать, что существуют некоторые общие принципы, которые следует использовать при разработке программ. Частотный принцип. Принцип основан на выделении в алгоритмах и данных особых групп по частоте использования. Для действий, наиболее часто встречающихся при работе программ, создаются условия их быстрого выполнения. К часто используемым данным обеспечивается наиболее быстрый доступ. «Частые» операции стараются делать более короткими. Следует отметить, что лишь не более 5 % операторов программы оказывают ощутимое влияние на скорость выполнения программы. Этот факт позволяет значительную часть операторов программы кодировать без учета скорости вычислений, обращая основное внимание при этом на «красоту» и наглядность текстов. Принцип модульности. Под модулем в данном контексте понимают функциональный элемент рассматриваемой системы, имеющий оформление, законченное и выполненное в пределах требований системы, и средства сопряжения с подобными элементами или элементами более высокого уровня данной или другой системы. Способы обособления составных частей программ в отдельные модули могут различаться существенно. В значительной степени разделение системы на модули определяется используемым методом проектирования программ. Принцип функциональной избирательности. Этот принцип является логическим продолжением частотного и модульного принципов и используется при проектировании программ. В программах выделяется некоторая часть важных модулей, которые постоянно должны быть в состоянии готовности для эффективной организации вычислительного процесса. Эту часть в программах называют ядром или монитором. При формировании состава монитора требуется учесть два противоречивых требования. В состав монитора, помимо чисто управляющих модулей, должны войти наиболее часто используемые модули. Количество модулей должно быть таким, чтобы объем памяти, занимаемой монитором, был не слишком большим. Программы, входящие в состав монитора, постоянно хранятся в оперативной памяти. Остальные части программ постоянно хранятся во внешних запоминающих устройствах и загружаются в оперативную память только при необходимости, перекрывая друг друга также при необходимости. Принцип генерируемости. Основное положение этого принципа определяет такой способ исходного представления программы, который бы позволял осуществлять настройку на конкретную конфигурацию технических средств, круг решаемых проблем, условия работы пользователя. Принцип функциональной избыточности. Этот принцип учитывает возможность проведения одной и той же работы различными средствами. Особенно важен учет этого принципа при разработке пользовательского интерфейса для выдачи одних и тех же данных разными способами вызова из-за психологических различий в восприятии информации. Принцип «по умолчанию». Применяется для облегчения организации связей с системой как на стадии генерации, так и при работе с уже готовыми программами. Принцип основан на хранении в системе некоторых базовых описаний структур, модулей, конфигураций оборудования и данных, определяющих условия работы с программой. Эту информацию программа использует в качестве заданной по умолчанию, если пользователь забудет или сознательно не конкретизирует её. 15. Итерационные методы решения линейных алгебраических уравнений: метод Зейделя. СЛАУ-система m линейных алгебраических уравнений с n неизвестными вида: 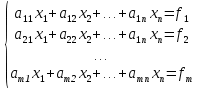 (1) (1)m-количество уравнений, n-количество неизвестных, x1…xn-неизвестные, которые надо найти, a11…amn-коэффициенты системы, fm-свободные члены. 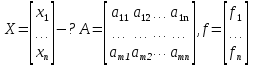 СЛАУ (1) в матричном виде Аx=f СЛАУ (1) в матричном виде Аx=fИтерационные методы устанавливают процедуру многократного уточнения определенного начального приближения к решению. Верхним индексом в скобках обозначается номер итерации(совокупность повторяющихся действий). Идея метода Зейделя при нахождении i-й компоненты (k+1)-го приближения сразу используються уже найденные компоненты (k+1)-го приближения с меньшими номерами 1,2,…,i-1.Применим для n*n систем. Рассмотрим стационарную схему 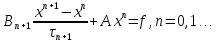 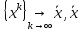 - точное решение - точное решениеА=А1+D+А2 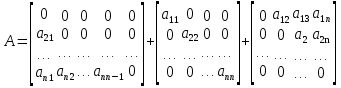 Bn+1=D+A1 , τn+1=1, (D+A1)(xn+1-xn)+Axn=f Bn+1=D+A1 , τn+1=1, (D+A1)(xn+1-xn)+Axn=f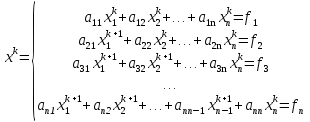 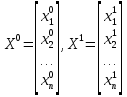 … …Теорема 1 (достаточное условие сходимости) 1. А=АТ (матрицы симметричны) 2.А>0 (Ах,х)>0, любого х≠0 Если 1,2 выполняются тогда метод Зейделя сходиться. 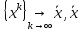 - точное решение - точное решение1. Преобразовать систему Ax=b к виду x=αx+β одним из описанных способов. 2. Задать начальное приближение решения 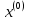 произвольно или положить произвольно или положить 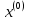 =β, а также малое положительное число e (точность). Положить k=0. 3. Произвести расчеты по формуле (10.15) или (10.16) и найти =β, а также малое положительное число e (точность). Положить k=0. 3. Произвести расчеты по формуле (10.15) или (10.16) и найти 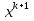 . 4. Если выполнено условие окончания . 4. Если выполнено условие окончания 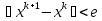 , процесс завершить и в качестве приближенного решения задачи принять , процесс завершить и в качестве приближенного решения задачи принять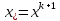 . Иначе положить k=k+1 и перейти к пункту 3. 16. Интерполяция многочленами: метод Лагранжа Интерполяция – определение промежуточных значений функции по известному дискретному набору значений функции. . Иначе положить k=k+1 и перейти к пункту 3. 16. Интерполяция многочленами: метод Лагранжа Интерполяция – определение промежуточных значений функции по известному дискретному набору значений функции.
f(xs), xs≠xi, i=0,1…n 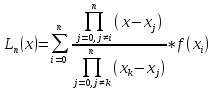 -Интерполяционная формула Лагранжа -Интерполяционная формула Лагранжа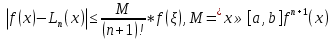 , , М- точная верхняя грань Теорема Если f(x)-многочлен n-степени, тоf(x)=Ln(x) 17.Разностные схемы для уравнения теплопроводности. Рассмотрим смешанную краевую задачу -начальное распределение температуры , - распределение температуры на концах рассматриваемого отрезка в любой момент времени. Введем равномерную сетку ωn и ωτ: . h, τ – шаги по направлению x, t. Узел сетки имеет координаты ( 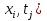 . Декартово произведение: . Декартово произведение: 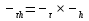 . Слоем называется множество узлов из . Слоем называется множество узлов из 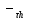 при фиксированном t. Существуют и основные схемы решения уравнения теплопроводности. 1) Явная схема. ДУ (1) заменяется сеточнымна 4-х точечном шаблоне вида: тогда уравнение (1) примет вид: при фиксированном t. Существуют и основные схемы решения уравнения теплопроводности. 1) Явная схема. ДУ (1) заменяется сеточнымна 4-х точечном шаблоне вида: тогда уравнение (1) примет вид: Начальные и граничные условия примут вид: Схема связывает 2 слоя и называется двухслойной. 2)Неявная схема Начальные и граничные условия примут вид: 3)Трехслойная схема Начальные и граничные условия примут вид: 4)Симметричная или шеститочечная Начальные и граничные условия примут вид: 18. Этапы принятия решений и решения проблем (1-5 этапы): информация, варианты, критерии, анализ вариант, процедура принятия решения. 1 этап. Осмысление и очерчивание проблемы. Необходимым условием к успеху является установление хороших человеческих отношений между держателем проблемы и исследователем. Осмыслением и очерчиванием проблемы является сбор информации,относящиеся к проблеме. 2 этап. Выявление возможных вариантов решения проблемы. Некоторое множество вариант как бы сами собой попадают в поле зрения. Этому способствует прошлый теоретический опыт. Теоретический опыт-образование. Для модельного описания вариант необходимо выделить управляемые и неуправляемые элементы(переменные). Управляемые и неуправляемые переменные могут быть качественными и некачественными. Лицо принимающее решение выбирает только один конкретный вариант наблюдения. Но есть иные варианты достижения цели. Поэтому на поиск вариант, которые сразу не бросились в глаза стоит потратить дополнительное время и силы. 3 этап. Определение критерия(-ев) оценки вариант. Следует всегда помнить, что неправильно выбранный критерий обязательно приведет к оптимальному решению. Критерий должен отражать суть работы. 4 этап. Анализ вариант по выбранному критерию. Анализ бывает двух типов: 1) качественный (применяется в случае отсутствия или недостаточного объема числовой информации. Информацию собирают в мнениях, ощущениях и предпочтениях); 2) количественный (применяется в случае достаточного объема числовой информации. При этом информация бывает двух типов: а) конкретная «о самом себе»; б) нечеткая, статистическая о влиянии внешней среды. Замечание: 1) качественный анализ всегда предшествует количественному; 2) любой анализ всегда проводится при некоторых допущениях, не искажающих решаемую проблему; 3) любой анализ всегда приближен, т.к. сказывается субъективизм всех предыдущих этапов. 5 этап. Процедура окончательного выбора перспективного решения проблем. Любая организация имеет иерархическую систему управления. Иерархическая структура управления порождается объективной потребностью в распределении обязанностей между людьми при решении общей задачи. Принятое решение закрепляется приказом. На его основе на нижних слоях системы управления издаются указы, распоряжения. Все это занимает время. Прежде чем выбранный вариант решения начнет реализовываться на практике. Принятое решение сразу не отменить. |
