Контрольная работа по ВМТС. Исследование и оптимизация системы автоматического регулирования частоты вращения вала двигателя постоянного тока. Задачи работы

• Название: Исследование и оптимизация системы автоматического регулирования частоты вращения вала двигателя постоянного тока. Задачи работы
• Анкор: Контрольная работа по ВМТС
• Дата: 05.02.2023
• Размер: 247.62 Kb.
• Имя файла: Контрольная работа по ВМТС.docx
• Тип: Исследование; #921092

Цель работы
Исследование и оптимизация системы автоматического регулирования частоты вращения вала двигателя постоянного тока.
Задачи работы

1. 
   Построение структурной схемы (модели САР)
   
2. 
   Построение частотных характеристик САР
   
3. 
   Анализ устойчивости и предварительная коррекция САР
   
4. 
   Оценка качества регулирования
   

Исходные данные
N – номер варианта; N = 6.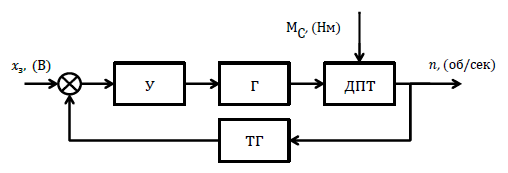



Рисунок 1 – функциональная схема системы
У – усилитель; Г – генератор постоянного тока; Д – двигатель постоянного тока; ТГ – тахогенератор; М_c – момент сопротивления на валу двигателя; n – частота вращения вала двигателя.
Параметры элементов

У (усилитель) – усилительное, пропорциональное звено: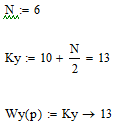


Г (генератор) – апериодическое звено: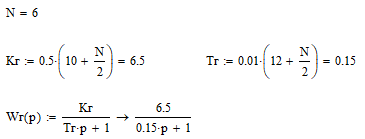


Д – двигатель постоянного тока. Модель двигателя по управлению – апериодическое звено второго порядка: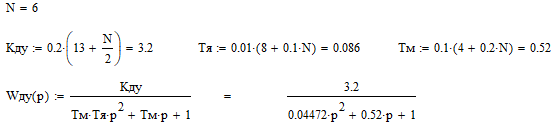


Д – двигатель по возмущению, моменту нагрузки, имеет параметры и передаточную функцию: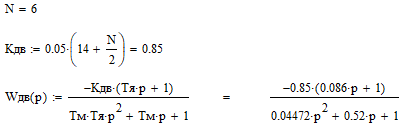


ТГ – пропорциональное звено: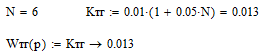


Ход работы
Зная ПФ отдельных элементов, составляем структурную схему САР: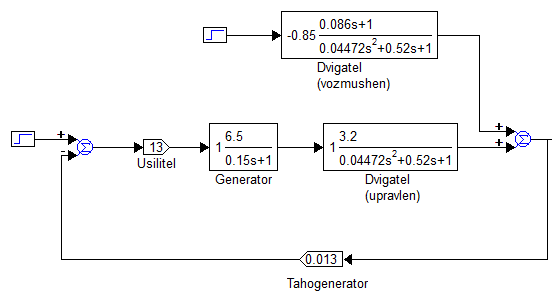



Рисунок 2 – Структурная схема САР
Выполним моделирование и определим основные показатели качества переходного процесса по каналу управления (Входное воздействие по каналу возмущения равно 0):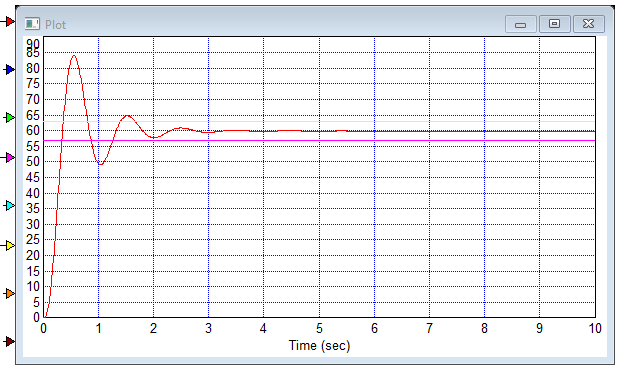



Рисунок 3 – Переходная характеристика нескорректированной замкнутой САР
Установившееся значение переходной характеристики составляет:

h(∞) ≈60об/сек.

Быстродействие САР характеризуется временем регулирования t_p,которое определяется моментом последнего входа переходной функции в 5% коридор около установившегося значения переходной функции. В нашем случае время регулирования t_p составляет 1,3 с.

Точность регулирования в переходном режиме характеризуется показателем качества, называемым перерегулирование – отношение разницы максимального значения переходной характеристики и установившегося значения переходной характеристики к установившемуся значению переходной характеристики (обычно указывается в процентах):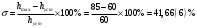


Точность работы САР в установившемся режиме тоже может быть оценена по рисунку. Учитывая величину коэффициента усиления тахогенератора, равную 0.013, можно сказать, что при безошибочной работе САР установившееся значение выходного сигнала (частоты вращения вала) составило бы 1/0,013 = 76,923 об/сек. На самом деле, как видно на рисунке 3, у исходной САР установившееся значение выходного сигнала составляет 60 об/сек. Относительная величина ошибки регулирования, при отслеживании постоянного сигнала составляет:



что считается слишком большой величиной. Для статических САР считается приемлемым

0.01 0< 0.1.

Таким образом, если качество регулирования рассматриваемой САР в переходном и установившемся режиме требует коррекции САР.

Коррекция может быть осуществлена изменением усиления контура регулирования, а если этого окажется недостаточно, то и введением ПИ-регулятора в контур.
Зная структурную схему САР рассчитаем ПФ по каналу управления и возмущения.



Рисунок 4 – Структурная схема САР
При расчёте ПФ по каналу управления полагаем, что возмущающий сигнал отсутствует: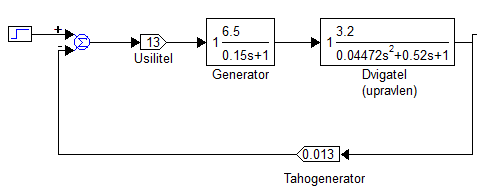



Рисунок 5 – Расчёт ПФ по каналу управления
Эквивалентная ПФ разомкнутой системы может быть рассчитана как произведение ПФ всех звеньев, последовательно включённых в замкнутый контур:




Эквивалентная ПФ замкнутой системы по каналу управления: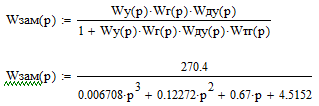


Далее определим ПФ замкнутой системы по ошибке канала управления. Поскольку главная отрицательная обратная связь неединичная, нужно сначала определить т.н. эквивалентную ПФ:



Где



Эквивалентные ПФ линии прямой цепи и контура обратной связи соответственно.

Тогда ПФ по ошибке может быть найдена по формуле: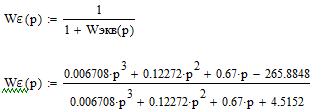


При расчёте ПФ по каналу возмущения полагаем, что управляющий сигнал отсутствует: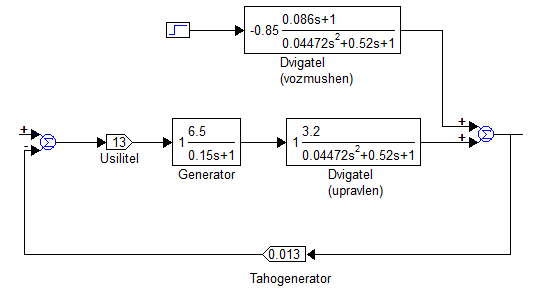



Рисунок 6 – Расчёт ПФ по каналу возмущения
Эквивалентная ПФ замкнутой системы по каналу возмущения: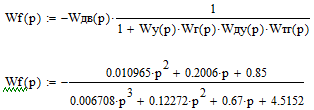



Обратим внимание, что во всех случаях при расчёте ПФ замкнутых систем знаменатели ПФ совпадают, что свидетельствует о правильности расчётов.

Разомкнём систему и построим логарифмические частотные характеристики по каналу управления.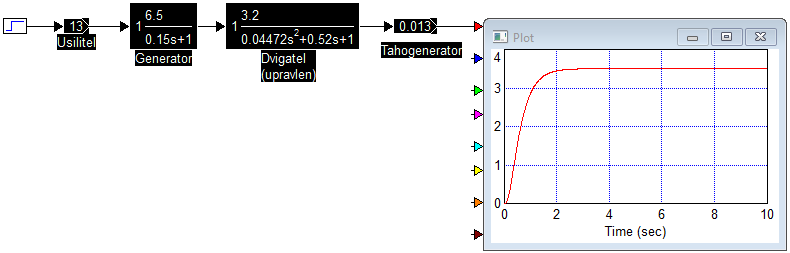



Рисунок 7 – Расчёт частотных характеристик
Выделив звенья, проходим по вкладке Analyze→FrequencyResponse и строим ЛАЧХ и ЛФЧХ разомкнутой системы: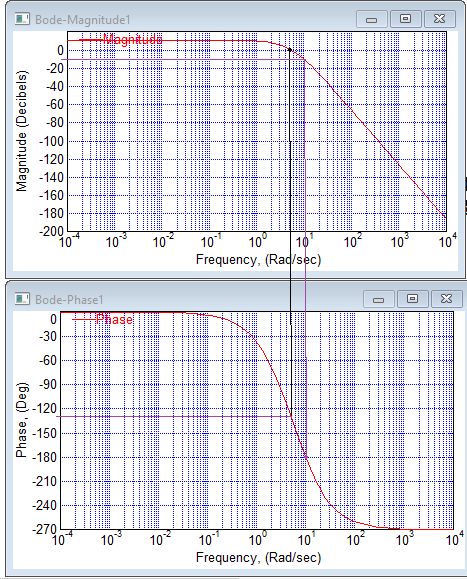



Рисунок 8 – ЛАЧХ и ЛФЧХ разомкнутой системы
Анализируя рисунок 8, определяем запасы устойчивости:

На частоте среза ЛАЧХ разомкнутой системы значение ЛФЧХ разомкнутой системы составляет φ(ω) = -130º. Следовательно, запас устойчивости по фазе составляет: Δφ = 180º - 130º = 50º.

На критической частоте ЛФЧХ значение ЛАЧХ составляет L(ω) = -10дБ. Следовательно, запас устойчивости по модулю составляет 10 дБ.

Запасы устойчивости достаточны. Введём в систему ПИ-регулятор


Из рисунка 8 определяем, что частота пересечения низкочастотной асимптоты ЛАЧХ и касательной под наклоном «-20 дБ/дек» составляет ω = 2. Ей соответствует постоянная времени T_p = 1/2 = 0,5.

Оптимальным коэффициентом передачи ПИ-регулятора, при котором перерегулирование не будет превышать 5% является значение 0,3: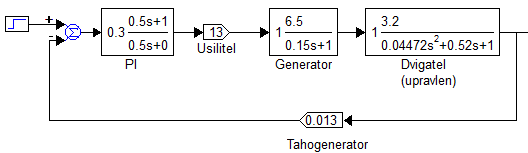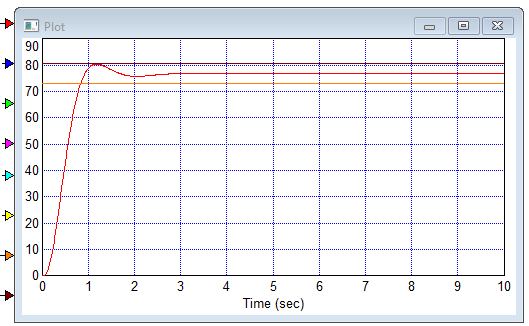





Рисунок 9 – Моделирование системы с ПИ-регулятором

Далее разомкнём систему и определим запасы устойчивости системы с ПИ-регулятором:



Рисунок 10 – Разомкнутая система с ПИ-регулятором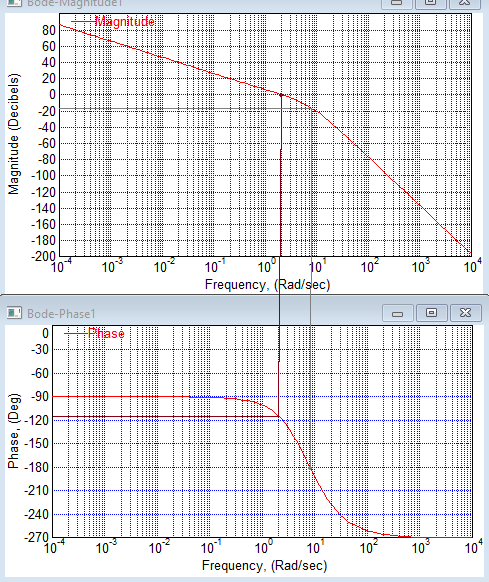


Рисунок 11 – ЛАЧХ и ЛФЧХ системыс ПИ-регулятором
Анализируя рисунок 11, определяем запасы устойчивости:

На частоте среза ЛАЧХ разомкнутой системы значение ЛФЧХ разомкнутой системы составляет φ(ω) = -115º. Следовательно, запас устойчивости по фазе составляет: Δφ = 180º - 115º = 65º.

На критической частоте ЛФЧХ значение ЛАЧХ составляет L(ω) = -18дБ. Следовательно, запас устойчивости по модулю составляет 18 дБ.