Курсовая по основам автоматизации. Уравнения динамики сар
 Скачать 477.91 Kb. Скачать 477.91 Kb.
|
Оглавление [1]Введение 2 1.Уравнения динамики САР 3 2.Структурная схема САР 4 3. Характеристическое уравнение САР 5 4.Определение значения коэффициента настройки САР 7 5. Графики переходной характеристики САР [2] 8 6. Графики фазовых портретов 10 Заключение 12 Список использованных источников 13 Приложение 14 ВведениеОбъект исследования: Система автоматического регулирования (САР): машина-двигатель (без свойства саморегулируемости) со статическим регулятором прямого действия (регулятором Уатта). В регуляторе также используется принцип управления по скорости (принцип Сименсов). Заданные параметры: 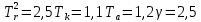 Задание: Дать уравнения динамики САР. Представить структурную схему САР. Записать характеристическое уравнение САР. Используя критерий Вышнеградского, определить значения коэффициента настройки САР (коэффициент Td ), при котором САР будет устойчивой. Получить и представить графики переходной характеристики в САР для случаев: а) когда САР устойчива; б) когда САР неустойчива. Получить и представить графики фазового портрета в САР для случаев: а) когда САР устойчива; б) когда САР неустойчива. Сделать необходимые выводы и заключения. Уравнения динамики САР Уравнение машины-двигателя: 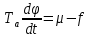 , (1) , (1)Где: 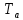 – положительный коэффициент, характеризующий инерционные свойства объекта регулирования – положительный коэффициент, характеризующий инерционные свойства объекта регулирования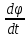 или или 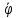 – производная от времени от – производная от времени от 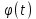 (скорость изменения регулируемой величины) (скорость изменения регулируемой величины)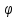 - регулируемая переменная (относительное изменение частоты вращения) - регулируемая переменная (относительное изменение частоты вращения)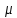 – управляющее воздействие на объект – управляющее воздействие на объект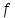 - возмущающее воздействие - величина, характеризующая относительное изменение нагрузки - возмущающее воздействие - величина, характеризующая относительное изменение нагрузкиУравнение регулятора Уатта: 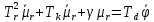 + + 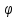 (2) (2)Где: 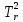 –положительный коэффициент, характеризующий инерционные свойства регулятора –положительный коэффициент, характеризующий инерционные свойства регулятора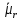 – вторая производная от – вторая производная от 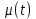 (ускорение регулирующего воздействия) (ускорение регулирующего воздействия)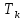 – коэффициент, характеризующий демпфирующие свойства – коэффициент, характеризующий демпфирующие свойства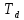 – коэффициент – коэффициентγ – коэффициент неравномерности регулятора. 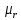 – выходная величина регулятора – выходная величина регулятораУравнение обратной связи: 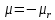 (3) (3)Структурная схема САР По данным выше дифференциальным уравнениям можно составить структурную математическую модель заданной автоматической системы (рис. 1) 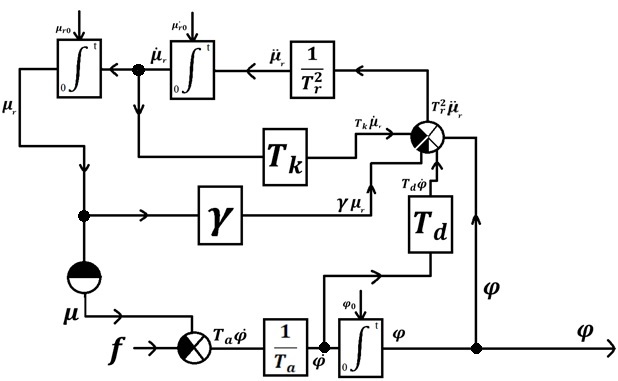 Рис. 1 Структурная схема САР 3. Характеристическое уравнение САР 1. Передаточная функция машины-двигателя: 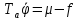 Запишем 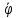 в другой форме, а в другой форме, а 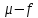 представим в виде 1 представим в виде 1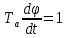 Обозначим дифференциал как 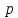 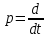 Обозначим 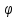 за за 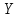 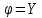 Обозначим 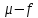 за за 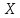 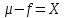 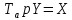 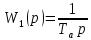 (4) (4)2. Передаточная функция регулятора Уатта: 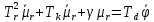 + + 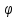 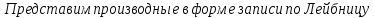 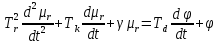 Обозначим дифференциал как 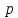 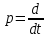 Обозначим 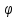 за за 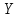 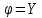 Обозначим 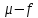 за за 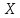 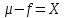 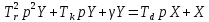 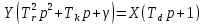 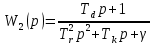 (5) (5)3. Объект регулирования и регулирующее устройство соединяются через отрицательную обратную связь, поэтому передаточную функцию САР можно найти по формуле: 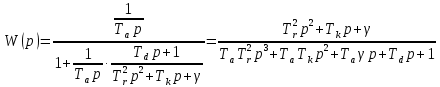 (6) (6)Характеристическим уравнением будет являться знаменатель уравнения номер 6 приравненный к нулю: 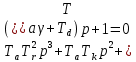 (7) (7)Определение значения коэффициента настройки САР После подстановки значений в уравнение (7) получается следующее характеристическое уравнение: 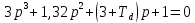 (8) (8)Значения коэффициента настройки определяются с помощью критерия Вышнеградского: 1. Необходимое условие устойчивости: 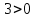 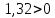 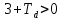 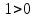 Следовательно, коэффициент 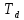 должен находиться в интервале (-3; +∞) должен находиться в интервале (-3; +∞)2. Достаточное условие устойчивости: Для устойчивой системы: 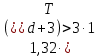 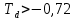 Исходя из этого, коэффициент 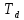 должен находиться в инетрвале должен находиться в инетрвале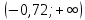 5. Графики переходной характеристики САР [2]а) Для получения устойчивой системы, берем коэффициент 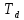 , согласно условию из пункта 4 , согласно условию из пункта 4 возьмем возьмем 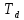 равным 0,1, результат подтверждаем графиком: [3] равным 0,1, результат подтверждаем графиком: [3]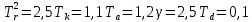 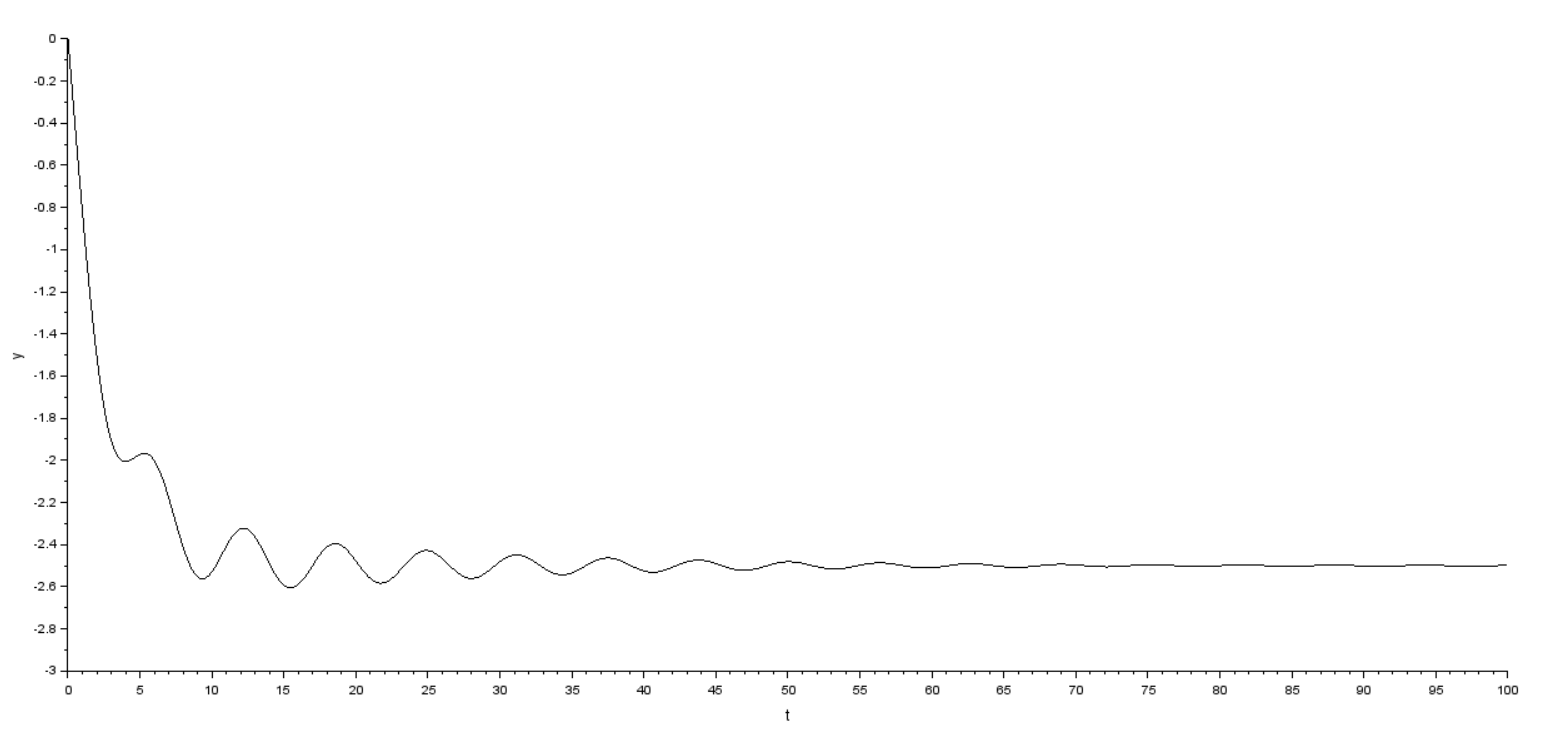 Рис. 2 График переходной характеристики устойчивой системы б) Для неустойчивой системы возьмем коэффициент 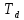 равным -1, результат подтверждаем графиком: равным -1, результат подтверждаем графиком: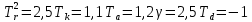 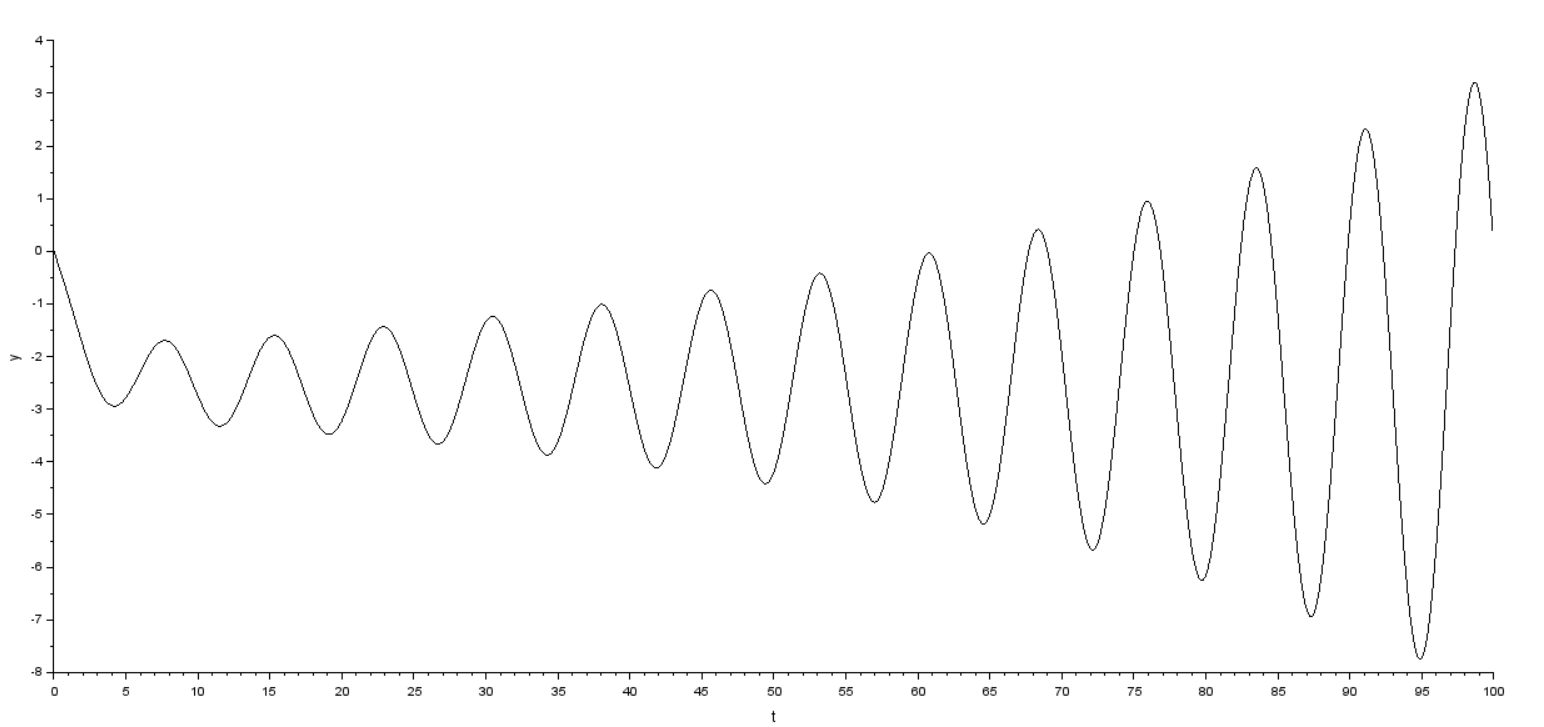 Рис. 3 График переходной характеристики неустойчивой системы 6. Графики фазовых портретова) Для построения фазового портрета устойчивой системы возьмем такой же коэффициент 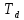 как для графика переходного процесса устойчивой системы: как для графика переходного процесса устойчивой системы: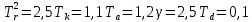 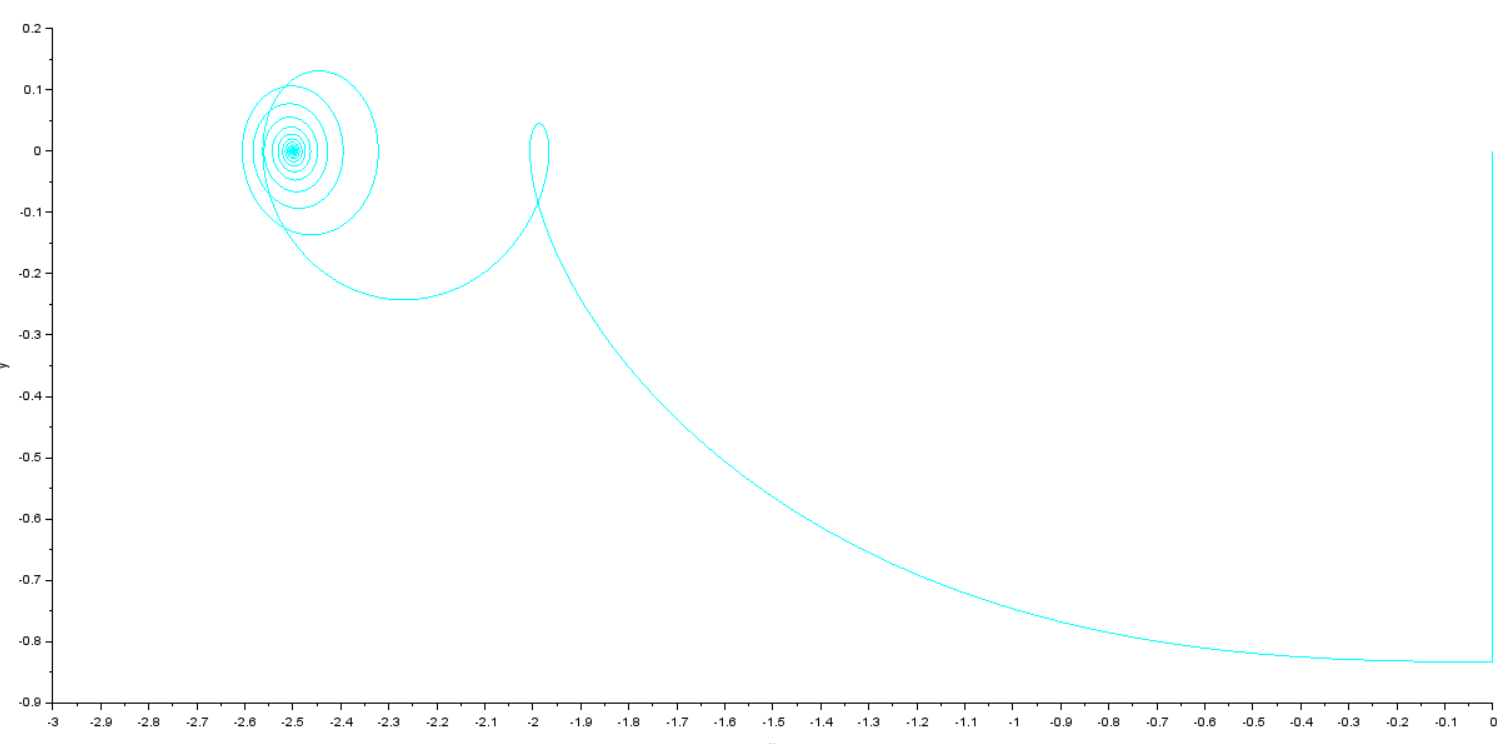 Рис. 4 Фазовый портрет устойчивой системы б) Для построения фазового портрета неустойчивой системы возьмем такой же коэффициент 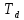 как для графика переходного процесса неустойчивой системы: как для графика переходного процесса неустойчивой системы: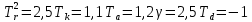  Рис. 5 Фазовый портрет неустойчивой системы ЗаключениеВ ходе исследования мы представили уравнения динамики САР (уравнение машины-двигателя, уравнение регулятора Уатта, уравнение обратной связи). Затем по ним была составлена структурная схема САР (рис. 1), объединяющая в себе уравнения из п. 1. В п. 4 была найдена область допустимых значений коэффициента Td (для устойчивой системы) по критерию Вышнеградского с помощью характеристического уравнения, найденным в пункте 3. В п. 5 и 6 были построены графики переходной характеристики и фазового портрета для устойчивой и неустойчивой системы. В результате исследований, были получены следующие выводы: система будет устойчивой, если коэффициент Tdбудет больше -0.72, что было рассчитано по критерию Вышнеградского под пунктом 4. На графике в пункте 5а (график переходной характеристики для устойчивой системы) наглядно видно, что система устойчива, так как график оканчивается установившимся режимом. В пункте 6а (фазовый портрет для устойчивой системы) хорошо просматривается устойчивая система, так какфазовый портрет закручивается по часовой стрелке Аналогично, мы можем наблюдать неустойчивую систему по тем же пунктам. При коэффициентеTd, меньшим -0.72, так же рассчитанным по критерию Вышнеградского в пункте 4, график переходного процесса (пункт 5б) не будет оканчиваться установившимся режимом, а фазовый портрет (пункт 6б) будет раскручивается по часовой стрелке. Все поставленные цели и задачи курсовой работы успешно выполнены. Список использованных источниковГОСТ 7.32—2017 ОТЧЕТ О НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЕ Структура и правила оформления (https://www.rea.ru/ru/org/managements/orgnirupr/Documents/gost_7.32-2017.pdf) Программное обеспечение с открытым исходным кодом для численных вычислений (https://www.scilab.org/ Исследование непрерывных и цифровых систем управления в среде Scilab (https://kpolyakov.spb.ru/uni/scibook.htm) Приложение Рис. 1 Схема переходной характеристики устойчивой системы (для рис. 2)  Рис. 2 Схема переходной характеристики для неустойчивой системы (для рис. 3)  Рис. 3 Схема фазового портрета устойчивой системы (для рис. 4) 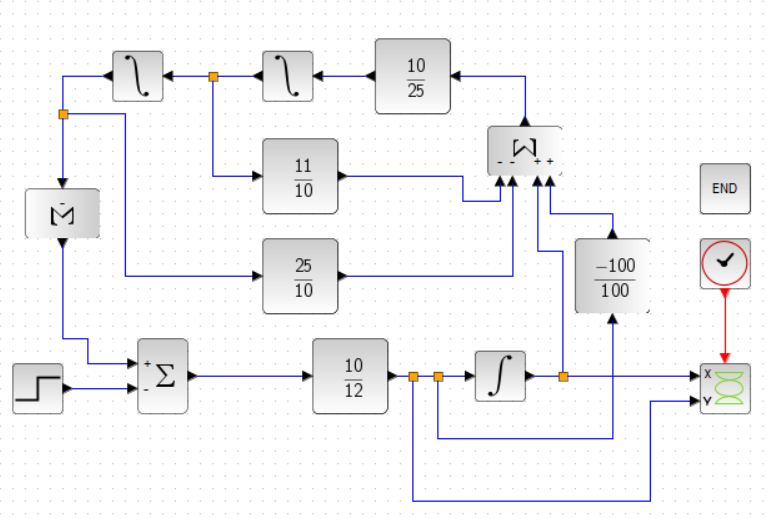 Рис. 4 Схема фазового портрета неустойчивой системы (для рис. 5) |
