Ряды в комплексной области. Исследование комплексных рядов 20 заключение 28 список литературы 29

• Название: Исследование комплексных рядов 20 заключение 28 список литературы 29
• Анкор: Ряды в комплексной области
• Дата: 28.02.2021
• Размер: 0.56 Mb.
• Имя файла: 000160f6-7072cdd0.docx
• Тип: Исследование; #180493
• страница: 2 из 3

ТЕОРИЯ ВЫЧЕТОВ

Вычетом функции f(z) в изолированной особой точке z₀ (точка принадлежит области комплексных чисел) называется интеграл вида:

где  - контур, принадлежащий окрестности точки z₀ и охватывающий ее. Обход контура - положительный, т.е. область ограниченная им и принадлежащая окрестности z₀ при обходе расположена слева: обход против часовой стрелки.

Обозначается вычет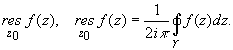 

                              

Вычет функции в конечной изолированной особой точке равен коэффициенту С_-1 при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при 1/(z-z₀) для z₀, принадлежащей области комплексных чисел:     

Теория вычетов опирается на  интегральную теорему Коши. Основной в теории вычетов является следующая теорема о вычетах. Пусть /(z) - однозначная аналитическая функция всюду в односвязной области G, кроме изолированных особых точек; тогда интеграл от f(z) по любой простой замкнутой спрямляемой кривой g, лежащей в области G и не проходящей через особые точки функции f(z), вычисляется но формуле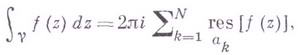 



где   - особые точки функции  , попавшие внутрь  .

Вычет функции в бесконечно удаленной точке   для функции  , однозначной и аналитической в окрестности этой точки, определяется формулой 



где  - окружность достаточно большого радиуса, ориентированная по часовой стрелке, а  - коэффициент при   в разложении Лорана функции   в окрестности этой точки.

Из теоремы о вычетах вытекает теорема о полной сумме вычетов: если f(z)- однозначная аналитическая функция в расширенной комплексной плоскости, кроме конечного числа особых точек, то сумма всех вычетов функции  , включая вычет в бесконечно удаленной точке, равна нулю.

Таким образом, вычисление интегралов от аналитич. функций по замкнутым кривым (контурных интегралов) сводится к вычислению В., к-рые находятся особенно просто в случае конечных полюсов. Пусть 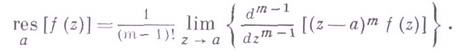  - полюс порядка т функции  , тогда 



При m=1 (простой полюс) эта формула принимает вид 



если   регулярны в окрестности точки а, причем для   точка а есть простой нуль, то

 .

Применение теоремы о вычетах к логарифмической производной приводит к важной теореме о логарифмическом вычете: если функция   мероморфна в односвязной области G, а простая замкнутая кривая   лежит в Gи не проходит через нули и полюсы функции  , то 



где N - число нулей, Р - число полюсов функции   внутри   с учетом их кратностей. Выражение в левой части этой формулы наз. логарифмическим вычетом функции относительно кривой.

В. применяются к вычислению нек-рых определенных интегралов от действительных функций, таких, напр., как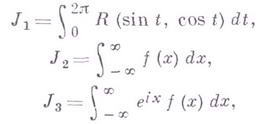 



где   -рациональная функция от   непрерывная при  - непрерывная функция при   где   - мнимая часть z, и аналитическая при   кроме конечного числа особых точек. При этом   подстановкой   сводится к контурному интегралу 



т. е. к вычислению В.;



если 



если f (z) удовлетворяет условиям Жордана леммы.

Вычеты находят многочисленные и важные применения в вопросах аналитического продолжения, разложения мероморфных функций на простейшие дроби, суммирования степенных рядов, асимптотических оценок и во многих др. вопросах анализа и его приложений (см. |1] - [4]).

Теория В. одного переменного разработана в основном О. Коши (A. Cauchy) в 1825 - 29. Ряд результатов, относящихся к обобщениям теории В. и ее приложениям, был получен Ш. Эрмитом (Ch. Hermite, теорема о сумме вычетов двоякопериодической функции), П. Лораном (P. Laurent), Ю. В. Сохоцким, Э. Линделёфом   и др.

На римановой поверхности рассматриваются вычеты не аналитических функций, а аналитических дифференциалов (см. [5]). Вычет аналитического дифференциала   в окрестности его изолированной особой точки определяется как коэффициент   при   в разложении Лорана функции   где   - униформизирующий параметр в окрестности этой точки. При этом интеграл от dZ но любой замкнутой кривой на римановой поверхности выражается через вычет дифференциала dZ и через его циклические периоды (интегралы от dZ по каноническим разрезам]. На римановы поверхности распространяется теорема о полной сумме вычетов: сумма всех вычетов мероморфного дифференциала на компактной римановой поверхности равна нулю.

Теория вычетов аналитических функций многих комплексных переменных базируется на интегральных теоремах Стокса и Коши - Пуанкаре, позволяющих заменять интеграл от замкнутой формы по одному циклу интегралом от этой формы по другому циклу, гомологичному первому. Начало теории вычетов функции многих переменных положил А. Пуанкаре [6], к-рый в 1887 впервые обобщил интегральную теорему Коши и понятие вычета на функции двух комплексных переменных, показав, в частности, что интеграл от рациональной функции двух комплексных переменных по двумерному циклу, не проходящему через особенности подинтегральной функции, сводится к периодам абелевых интегралов, и применил двойные вычеты для обоснования двумерного аналога Лагранжа ряда.