Ряды в комплексной области. Исследование комплексных рядов 20 заключение 28 список литературы 29
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
ПРАКТИЧЕСКОЕ ИССЛЕДОВАНИЕ КОМПЛЕКСНЫХ РЯДОВНайти область сходимости рядов: 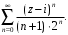 Решение: Здесь 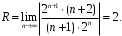 Данный ряд сходится в области Данный ряд сходится в области 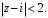 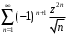 и исследовать сходимость ряда в точках и исследовать сходимость ряда в точках 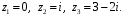 Решение: Здесь 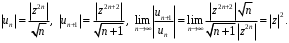 Ряд сходится при всех Ряд сходится при всех  , удовлетворяющих неравенству , удовлетворяющих неравенству 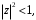 т. е. т. е. 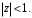 Кругом сходимости является круг с центром в точке Кругом сходимости является круг с центром в точке 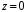 и радиусом равным 1. и радиусом равным 1.Точка 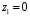 лежит внутри круга сходимости, в этой точке ряд сходится абсолютно. Точка лежит внутри круга сходимости, в этой точке ряд сходится абсолютно. Точка 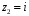 лежит на границе круга сходимости, в этой точке ряд может сходится (абсолютно или условно) и расходиться. Подставляя значение лежит на границе круга сходимости, в этой точке ряд может сходится (абсолютно или условно) и расходиться. Подставляя значение 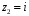 в выражение общего члена ряда, получим в выражение общего члена ряда, получим 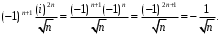 Числовой ряд с общим членом Числовой ряд с общим членом 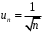 расходится согласно интегральному признаку Коши. Следовательно, в точке расходится согласно интегральному признаку Коши. Следовательно, в точке 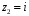 степенной ряд степенной ряд 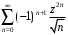 расходится. расходится.Точка 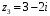 лежит вне круга сходимости, ряд в этой точке расходится. лежит вне круга сходимости, ряд в этой точке расходится.Записать разложение по степеням z функции f (z) = ch z. Найдем производные функции: f (n) (z) = ch(n) z = ch z при n = 2k, f (n) (z) = ch(n) z = sh z при n = 2k-1. В данном примере z0 = 0. По формуле (3) имеем: Cn = 0 при n = 2k; Cn = 1/n! при n = 2k-1; . Так как ch z - аналитическая функция в области действительных чисел, то радиус R равен бесконечности. В результате имеем: (z принадлежит области действительных чисел). Разложить по степеням (z-3) функцию f(z) = sin z. Обозначим z-3 = t. Используя тригонометрическую формулу для функции sin (3+t), получим: sin(3+t) = sin3 cos t+cos3 sin t. Используя основные разложения, имеем: 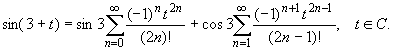 Так как t = z-3, то 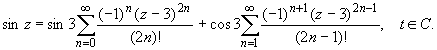 т.е. где Разложить функцию в ряд Лорана по степеням z. Решение.Так как функция является рациональной дробью, то особыми точками являются нули знаменателя, т.е. z1 = -1 и z2 = 3. Запишем функцию в виде Кольца аналитичности | z | < 1, 1 < | z | < 3, | z | > 3. Раскладываем дробь на элементарные дроби: При | z | < 1 имеем: 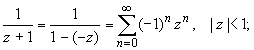 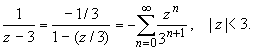 Таким образом, в круге | z | < 1 функция раскладывается в ряд Тейлора: 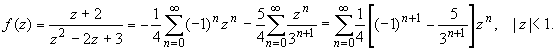 В кольце 1 < | z | < 3: 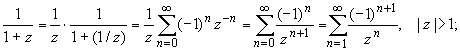 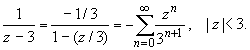 В итоге имеем: 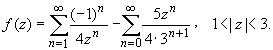 В круге | z | > 3: 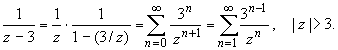 В итоге имеем: 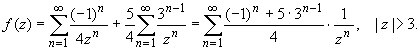 Разложить функцию f(z) = z3·e1/z в окрестности точки z0 = 0. Решение.Из основного разложения получаем Или 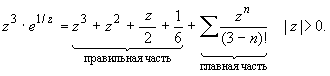 Вычислить вычет функции f (z) = (z+2)/(z2-2z-3) в точке z = 3. Решение. Разложим функцию в ряд Лорана по степеням z - 3: 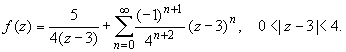 Из этого разложения находим Заметим, что здесь точка z = 3 - простой полюс. Вычислить вычет функции f(z) в точке z = 0, Решение. Запишем 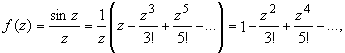 т.е. z = 0 - устранимая особая точка. Следовательно, Вычислить вычет функции Так как 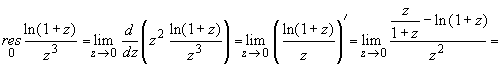 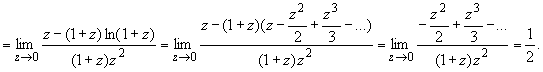 Вычислить вычет функции f(z) = ctg 2z во всех ее особых точках. Решение. В точках данная функция имеет полюсы первого порядка (простые полюсы), поскольку Следовательно, 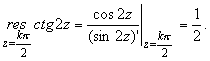 Вычислить вычет функции Решение. Разложим замкнутую функцию в ряд Лорана в окрестности z = 1: 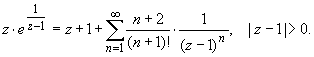 Из этого разложения следует, что z = 1 является существенной особой точкой и С -1 = 3/2, т.е. Разложить функцию Решение. Найдем коэффициенты Фурье: Поскольку = Искомое разложение будет иметь вид где учтено, что Применяя к ряду (25) равенство Парсеваля можно найти сумму еще одного числового ряда. Действительно, в нашем случае Тогда из (26) следует Принята, особенно в электротехнике и радиотехнике, следующая терминология. Выражения Ряды Фурье применяются при разработке радиоэлектронных систем управления и наведения различных зенитно-ракетных комплексов, космических аппаратов, при расчетах заданных параметров управления полетом. Представить рядом Фурье в комплексной форме функцию 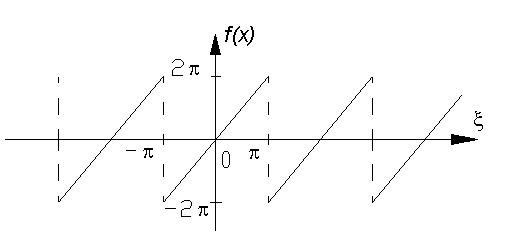 Рисунок 1 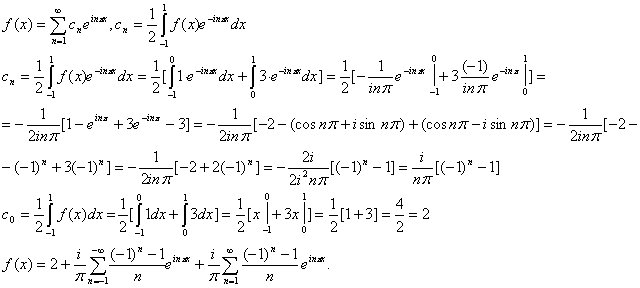 ЗАКЛЮЧЕНИЕПервая часть работы базируется на фундаментальных трудах по функциональному анализу и теории функций комплексного переменного, в ней даны основные понятия и определения, доказаны базовые теоремы, содержащие сведения о комплексных рядах. Вторая глава включает в себя анализ теории вычетов и применение рядов к вычислению вычетов аналитических функций. В третьей главе даны примеры практического применения рассмотренных теорий. СПИСОК ЛИТЕРАТУРЫ1. Араманович И.Г., Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. - М.: Наука, 1966.-331с. 2. Волков И.К., Канатников А.Н. Интегральные преобразования и операционное исчисление. Учебник для вузов (под ред. В.С.Зарубина и А.П. Крищенко). – М.: МГТУ, – 1996. (Серия «Математика в техническом университете», вып. XI). 3. Волковыский Л. И., Лунц Г. Л., Араманович И. Г. Сборник задач по теории функций комплексного переменного. М.: ФИЗМАТЛИТ, 2002. 4. Демидович Б. П. Сборник задач и упражнений по математическому анализу. 13-е издание, испр. М.: Изд-во Моск. ун-та, ЧеРо, 1997. 5. Евграфов М. А. и др. Сборник задач по теории аналитических функций. М.: Наука, физ.-мат. лит., 1972. 6. Краснов М.Л., Киселев А.И., Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. Задача и упражнения. – М.: Наука, 1981. – 215с. 7. Мышкис А.Д. Математика для втузов. Специальные курсы. – М.: Наука, 1971. – 632с. 8. Сборник задач по математике для втузов. Специальные разделы математического анализа. Под ред.Ефимова А.В., Демидовича Б.П., т.2. – 2-е изд. - М.: Наука, 1986.-368с. 9. Смирнов В.И. Курс высшей математики. Т.2. – М.: ГИФМЛ, 1961. – 628с. 10. Шостак Р.Я. Операционное исчисление. М.: Высшая школа. – 1972. - 252с. |
