Ряды в комплексной области. Исследование комплексных рядов 20 заключение 28 список литературы 29
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
Титул ОГЛАВЛЕНИЕВВЕДЕНИЕ 3 ПОНЯТИЕ РЯДОВ В КОМПЛЕКСНОЙ ОБЛАСТИ 4 ТЕОРИЯ ВЫЧЕТОВ 16 ПРАКТИЧЕСКОЕ ИССЛЕДОВАНИЕ КОМПЛЕКСНЫХ РЯДОВ 20 ЗАКЛЮЧЕНИЕ 28 СПИСОК ЛИТЕРАТУРЫ 29 ВВЕДЕНИЕИсследование функциональных рядов позволяет решать множество прикладных задач. Наиболее широкое применение сегодня находит теория вычетов, которая применяется как в теоретических изыскания, так и в практических разработках, связанных с машиностроением, теорией упругости и многим другим. Несмотря на то, что данные теории уже давно изучены, прикладное применение использования рядов в комплексной области, а также теории вычетов все более расширяется. Целью работы является изучение теоретических и практических основ применения рядов в комплексной области. В ходе работы решаются следующие задачи: 1. Рассмотреть теоретические аспекты и базовые понятия комплексных рядов; 2. Проанализировать теоретическое применение рядов к теории вычетов; 3. Привести примеры анализа и решения задач по теме. ПОНЯТИЕ РЯДОВ В КОМПЛЕКСНОЙ ОБЛАСТИРяд 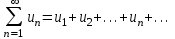 , (1) , (1)членами которого являются комплексные числа, называется числовым рядом (в комплексной области). Ряд (1) можно записать в виде 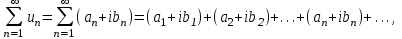 где 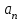 и и 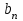 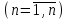 действительные числа. действительные числа.Сумма 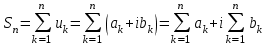 первых 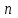 членов ряда (1) называется членов ряда (1) называется 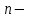 частичной суммой ряда. частичной суммой ряда.Если существует конечный предел 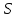 последовательности частичных сумм последовательности частичных сумм 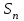 ряда: ряда: 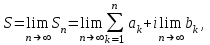 то ряд (1) называется сходящимся, а 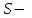 суммой ряда; если суммой ряда; если 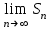 не существует, то ряд (1) называется расходящимся. не существует, то ряд (1) называется расходящимся.Очевидно, что ряд (1) сходится тогда и только тогда, когда сходится каждый из рядов 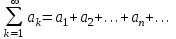 (2) (2)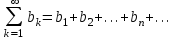 (3) (3)При этом 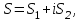 где где 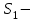 сумма ряда (2), а сумма ряда (2), а 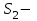 сумма ряда (3). Это означает, что исследование сходимости ряда с комплексными членами сводится к исследованию сходимости рядов (2), (3) с действительными членами. сумма ряда (3). Это означает, что исследование сходимости ряда с комплексными членами сводится к исследованию сходимости рядов (2), (3) с действительными членами. В теории рядов с комплексными членами основные определения, многие теоремы и их доказательства аналогичны соответствующим определениям и теоремам из теории рядов с действительными членами. Приведем некоторые из них. Теорема.(необходимый признак сходимости ряда). Если ряд (1) сходится, то его общий член 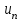 при при 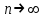 стремится к нулю, т.е. стремится к нулю, т.е. 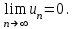 Ряд (1) называется абсолютно сходящимся, если сходится ряд 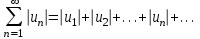 (3) (3)Теорема. Если сходится ряд (3), то абсолютно сходится ряд (1). При исследовании на сходимость рядов с комплексными членами применимы все известные из действительного анализа признаки сходимости знакопостоянных рядов. Признак Даламбера. Если существует 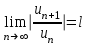 , то при , то при 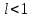 ряд (3) абсолютно сходится, а при ряд (3) абсолютно сходится, а при 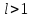 расходится. расходится.Степенным рядом в комплексной области называется ряд 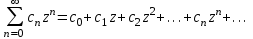 , (4) , (4)или ряд 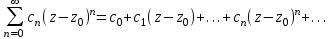 , (5) , (5)где 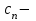 комплексные числа (коэффициенты ряда), комплексные числа (коэффициенты ряда), 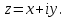 Ряды (4) и (5) при одних значениях аргумента 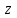 могут сходиться, при других расходиться. могут сходиться, при других расходиться. Совокупность всех значений 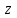 , при которых ряд (4) [(5)] сходится, называется областью сходимости этого ряда. , при которых ряд (4) [(5)] сходится, называется областью сходимости этого ряда.Теорема (Абеля). Если степенной ряд (4) сходится при 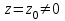 (в точке (в точке 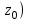 , то он абсолютно сходится при всех значениях , то он абсолютно сходится при всех значениях 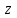 , удовлетворяющих условию , удовлетворяющих условию 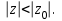 Следствие. Если ряд (4) расходится при 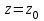 , то он расходится при всех значениях , то он расходится при всех значениях 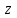 , удовлетворяющих условию , удовлетворяющих условию 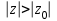 , т.е. вне круга радиуса , т.е. вне круга радиуса 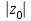 с центром в начале координат. с центром в начале координат.Из теоремы Абеля следует, что существует такое число 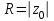 , что при всех , что при всех 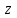 , для которых , для которых 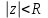 , степенной ряд (4) абсолютно сходится. Эти точки лежат на комплексной плоскости внутри круга радиуса , степенной ряд (4) абсолютно сходится. Эти точки лежат на комплексной плоскости внутри круга радиуса 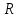 с центром в точке с центром в точке 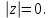 Величина 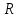 называется радиусом сходимости ряда, круг называется радиусом сходимости ряда, круг 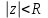 называется кругом сходимости ряда, вне этого круга ряд расходится, а на границе может как сходиться, так и расходиться. называется кругом сходимости ряда, вне этого круга ряд расходится, а на границе может как сходиться, так и расходиться.Если 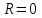 , то ряд (4) сходится в точке , то ряд (4) сходится в точке 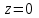 , если , если 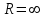 , то ряд сходится на всей комплексной плоскости. Для ряда (28) кругом сходимости является круг , то ряд сходится на всей комплексной плоскости. Для ряда (28) кругом сходимости является круг 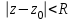 с центром в точке с центром в точке 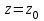 . .Радиус сходимости находится по формулам: 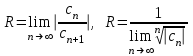 . .Свойства ряда (4), (5): Сумма степенного ряда внутри круга его сходимости есть аналитическая функция; Степенной ряд внутри круга сходимости можно почленно дифференцировать и почленно интегрировать любое число раз, полученный при этом ряд имеет тот же радиус сходимости, что и исходный ряд. Теоремаю Всякая аналитическая в круге 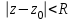 функция функция 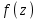 может быть единственным образом разложена в этом круге в степенной ряд может быть единственным образом разложена в этом круге в степенной ряд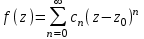 , (6) , (6)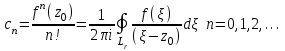 , (7) , (7)где 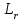 произвольная окружность с центром в точке произвольная окружность с центром в точке 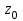 , лежащая внутри круга. , лежащая внутри круга.Степенной ряд (6) называется рядом Тейлора для функции 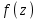 в рассматриваемом круге. в рассматриваемом круге.Приведем разложение некоторых элементарных функций в ряд Тейлора (Маклорена): 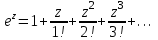 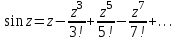 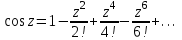 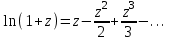 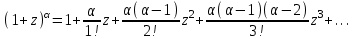 Первые три разложения справедливы во всех точках комплексной плоскости, последние два – в круге 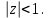 Заменив 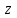 на на 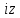 в разложении функции в разложении функции 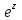 , получим: , получим: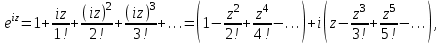 т.е. формулу Эйлера т.е. формулу Эйлера 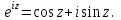 Теорема Тейлора (о разложении функции в степенной ряд). Функция, аналитическая в области комплексных чисел D, в окрестности каждой точки z0 этой области представляется в виде степенного ряда: 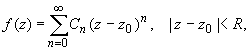 (7) (7)радиус сходимости R которого не меньше, чем расстояние от точки z0 до границы области D. Такой степенной ряд называется рядом Тейлора. Коэффициенты ряда Тейлора вычисляются по формуле: 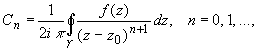 (8) (8)где - произвольный контур, принадлежащий области D и охватывающий точку z0 (в частности, - окружность ), или по формуле: (9) Радиус сходимости ряда Тейлора равен расстоянию от точки z0 до ближайшей особой точки функции. Для вычисления радиуса сходимости ряда Тейлора можно также использовать формулы: Основные разложения. (z принадлежит области комплексных чисел); (z принадлежит области комплексных чисел); (z принадлежит области комплексных чисел); (z принадлежит области комплексных чисел); (z принадлежит области комплексных чисел); 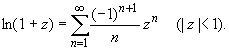 Теорема Лорана (о разложении функции в ряд по целым степеням). Функция f(z), аналитическая в кольце r < | z - z0 | < R, представляется в этом кольце сходящимся рядом по целым степеням, т.е. имеет место равенство: (10) Коэффициенты ряда вычисляются по формуле: 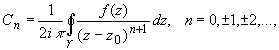 (11) (11)где - произвольный контур, принадлежащий кольцу и охватывающий точку z0; в частности, - окружность Ряд (10), коэффициенты которого вычисляются по формуле (11), называется рядом Лорана функции f(z). Совокупность членов ряда с неотрицательными степенями называется правильной частью ряда Лорана, члены с отрицательными степенями образуют главную часть ряда Лорана: или Для коэффициентов ряда имеет место формула оценки коэффициентов - неравенство Коши: где r - радиус контура интегрирования в формуле (11). На границах кольца сходимости ряда Лорана есть хотя бы по одной особой точке функции f(z) - его суммы. Частными случаями рядов Лорана являются разложения функции в окрестности особой точки z0 (r= 0) и в окрестности бесконечно удаленной точки (z0 = 0, ). При построении разложений в ряд Лорана используются разложения в степенные ряды (ряды Тейлора), используются основные разложения и арифметические операции со сходящимися рядами. Рассмотрим элементы теории рядов Фурье для комплексных функций, т.е. функций вида Скалярным произведением функций где 1. 2. билинейность Как и ранее, функции f и g будем называть ортогональными, если их скалярное произведение равно нулю. Определение нормы функции оставим прежним, так что Свойства нормы, претерпевшие изменения при переходе от вещественных функций к комплексным, следующие: 1. теорема косинусов. или в более общем виде 2. Обобщенная теорема Пифагора.Если 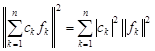 . .3. Неравенство Коши – Буняковского.Если функции В самом деле, если Таким образом, Пусть теперь система комплексных функций ортогональна на промежутке где коэффициенты Фурье 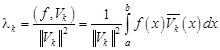 . .Введем обозначения: Тогда, так же, как для вещественных функций выполняется неравенство где Сходимость ряда в среднем и замкнутость системы функций определяются а) если для некоторой функции то ряд (14) сходится в среднем к б) ортогональная система функций (13) называется замкнутой на промежутке Введем в рассмотрение систему комплексных функций Свойства системы функции(17) следующие: 1. 2. Функции 3. Система функций (17) ортогональна на промежутке [–L , L ]. Действительно, при Здесь использована формула 4. Ряд Фурье для функции где коэффициенты Фурье 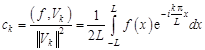 . (19) . (19)Система функций (17) замкнута на [–L , L ] , поэтому для нее справедливы следующие утверждения: а) ряд (18) сходится в среднем к б) для любой функции из в) среднеквадратическая погрешность, возникающая при замене функции Теорема Дирихле. Если вещественная и мнимая части функции Комплексная форма тригонометрического ряда Фурье Пусть вещественная функция где Если в (2.1) выразить 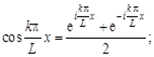 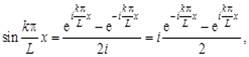 то получим ряд где в силу (22) = Последние три формулы можно объединить: Ряд (23) с коэффициентами (24) называется тригонометрическим рядом Фурье в комплексной форме. |
