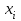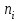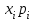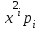Математическая статистика. Исследование продолжительности автомобильных рейсов (сутки). Результаты дорожной ведомости приведены в таблице 0
 Скачать 111.46 Kb. Скачать 111.46 Kb.
|
|
Математическая статистика В автопарке проводилось исследование продолжительности автомобильных рейсов (сутки). Результаты дорожной ведомости приведены в таблице 0 Таблица 0 4 2 7 10 4 3 6 2 8 10 2 8 5 6 3 4 8 6 5 1 5 7 4 3 4 7 3 5 9 2 3 5 10 4 3 8 5 9 4 4 4 7 4 2 1 8 10 3 4 6 1 3 6 2 4 7 5 5 0 2 3 7 7 9 10 2 5 8 3 6 8 10 2 4 9 3 6 6 2 7 9 3 5 2 1 6 3 5 7 2 10 5 7 3 6 3 2 7 1 9 Задание 1. Постройте статистический ряд. Задание 2. Вычислите относительные частоты и накопленные частоты. Задание 3. Представьте графически статистический ряд в виде полигона или гистограммы. Задание 4. Составьте эмпирическую функцию распределения. Задание 5. Постройте график эмпирической функции распределения. Задание 6. Вычислите точечные оценки параметров законов распределения: 1) выборочное среднее; 2) выборочную смещённую (неисправленную) дисперсию и выборочную несмещённую (исправленную) дисперсию; 3) выборочное неисправленное среднее квадратическое отклонение и выборочные исправленное среднее квадратическое отклонение; 4) выборочную моду; 5) выборочную медиану. Задание 7. Найдите доверительный интервал для неизвестного математического ожидания нормально рапсределенной генеральной совокупности при условии, что дисперсия неизвестна, если доверительная вероятность задана как 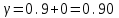 Решение. Задание 1,2 Минимальное значение 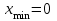 Максимальное значение Максимальное значение 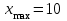 Объем выборки 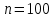 Относительная частота варианты Относительная частота варианты 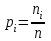 , , Накопленная частота: 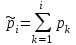 Строим статистический ряд, располагая в порядке возрастания возможные значения вариант. Второй столбец – частоты.
Задание 3. Представьте графически статистический рял в виде полигона или гистограммы. Строим полигон частот по первому и второму столбцу таблицы. 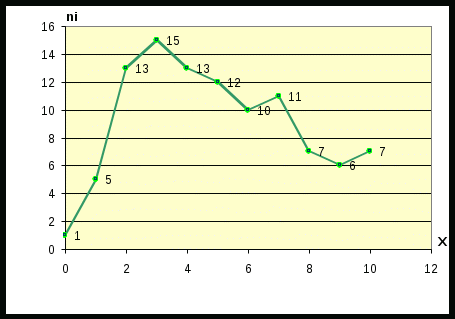 Задание 4. Составьте эмпирическую функцию распределения Построим гистограмму накопленных частот. 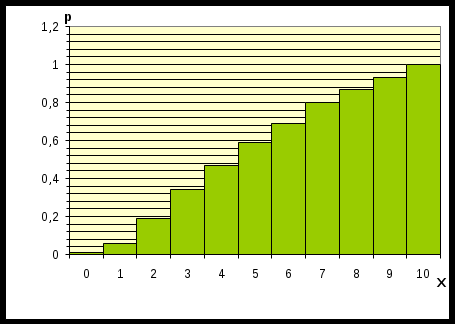 Используя накопленные частоты, запишем эмпирическую функцию распределения 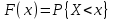 является кусочно-постоянной функцией. является кусочно-постоянной функцией.При 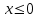 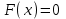 при 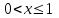 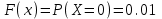 при 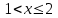 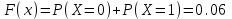 при 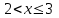 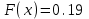 при 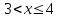 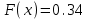 при 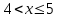 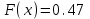 при 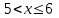 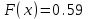 при 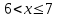 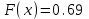 при 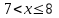 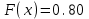 при 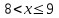 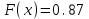 при 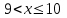 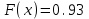 при 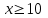 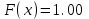 Задание 5. Постройте график эмпирической функции распределения 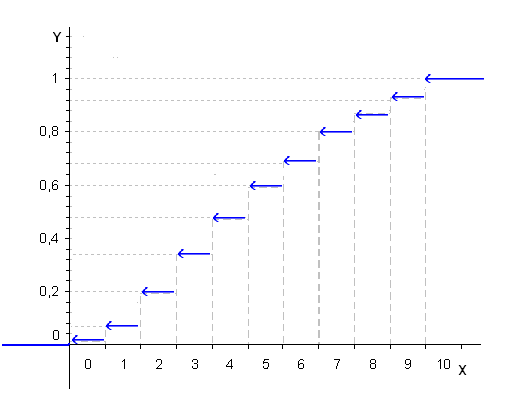 Задание 6 Вычислите точечные оценки параметров распределения Воспользуемся рассчетной таблицей
1) Выборочное среднее 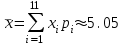 2) Выборочная смещенная (неисправленная) дисперсия 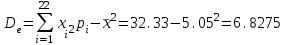 Исправленная выборочная дисперсия 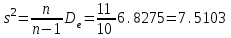 3) Неисправленное среднеквадратическое отклонение 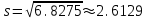 Исправленное среднеквадратическое отклонение 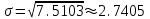 4) Выборочная модаравна значению варианты с наибольшей частотой 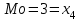 5) выборочная медиана равна значению варианты, стоящей в середине вариационного ряда, если число наблюдаемых вариант есть нечётное число 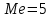 Задание 7. Найдите доверительный интервал для неизвестного математического ожидания нормально рапсределенной генеральной совокупности при условии, что дисперсия неизвестна, если доверительная вероятность задана как 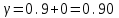 Решение Ранее вычислены выборочное среднее 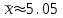 и иисправленное среднее квадратическое отклонение 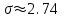 По условию 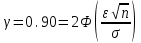 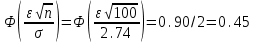 По таблице значений функции Лапласа находим значение аргумента 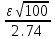 =1,64 =1,64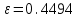 Таким образом, интервал ( 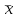 − 0,4494 ; − 0,4494 ; 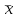 − 0,4494) = (4,6006; 5,4994) покрывает неизвестный параметр - математическое ожидание, с надёжностью − 0,4494) = (4,6006; 5,4994) покрывает неизвестный параметр - математическое ожидание, с надёжностью 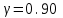 . . |