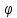Главная страница
Навигация по странице:

  • Лабораторная работа №2 по дисциплине «Электротехника»на тему«Исследование работы цепи однофазного синусоидального тока»

  • Опыт №1. Последовательное соединение катушки индуктивности и конденсатора. Резонанс напряжений. Таблица 1Результаты измерений

  • Опыт № 2. Параллельное соединение катушки индуктивности и конденсатора. Резонанс токов.

    		•

    Пономарев ЛР2. Исследование работы цепи однофазного синусоидального тока


    Скачать 1.1 Mb.
    НазваниеИсследование работы цепи однофазного синусоидального тока
    Дата10.10.2022
    Размер1.1 Mb.
    Формат файлаdocx
    Имя файлаПономарев ЛР2.docx
    ТипЛабораторная работа
    #725613

    МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
    ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

    ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

    «ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ»

    ИНСТИТУТ ПРОМЫШЛЕННЫХ ТЕХНОЛОГИЙ И ИНЖИНИРИНГА
    КАФЕДРА ЭЛЕКТРОЭНЕРГЕТИКИ


    Лабораторная работа №2

    по дисциплине «Электротехника»

    на тему

    «Исследование работы цепи однофазного синусоидального тока»
    Выполнил: Пономарев Константин группы НДб-19-6


    Проверил:

    ассистент кафедры ЭЭ

    Герасимов В. Е.



    Тюмень, 2021

    Цель работы: исследовать распределение токов, напряжений и мощностей при различных способах соединения катушки индуктивности и конденсатора. Определить условия наступления резонансного режима работы электрической цепи. Выявить особенности работы электрической цепи при резонансе. Экспериментально подтвердить законы Кирхгофа, закон Ома, баланс мощности для электрической цепи синусоидального тока.

    Опыт №1. Последовательное соединение катушки индуктивности и конденсатора. Резонанс напряжений.

    Таблица 1

    Результаты измерений


    N
    C, мкФ
    I, А
    UК, В
    UC, В
    P, Вт
    Q, вар
    S, ВА
    cos

    1
    40
    0,10
    2,7
    6,87
    0
    -0,3
    0,4
    0,16

    2
    60
    0,21
    5
    9,7
    0,2
    -0,8
    0,9
    0,32

    3
    80
    0,47
    12,9
    15,85
    1,3
    -1,5
    2,1
    0,65

    4
    100
    0,69
    18,2
    18,8
    2,9
    -0,7
    3,1
    0,96

    5
    120
    0,64
    17
    14,5
    2,6
    1,1
    28
    0,90

    6
    150
    0,44
    12,3
    8,7
    1,3
    1,3
    1,9
    0,7

    7
    180
    0,37
    10,4
    6,5
    0,9
    1,3
    1,7
    0,6

    8
    200
    0,33
    9,2
    5
    0,7
    1,2
    1,5
    0,53

    9
    300
    0,25
    7
    2,7
    0,4
    1
    1,1
    0,41




    1. Используя величины параметров таблицы 1 постройте и проанализируйте семейства зависимостей от емкости конденсатора:

    • тока электрической цепи I (C);

    • напряжения катушки индуктивности Uк (C) и конденсатора Uс (C);

    • активной P(C), реактивной Q(C) и полной S(C) мощностей;

    • коэффициента мощности cosφ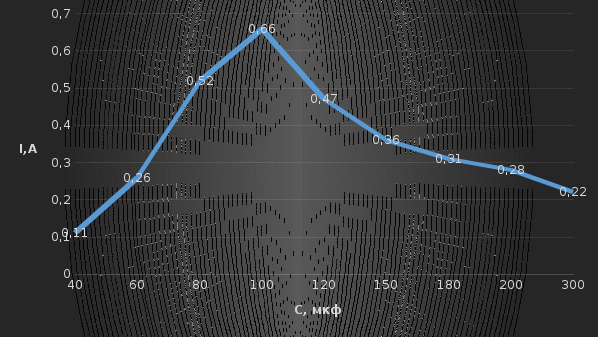






    Рис 1. – Зависимость силы тока электрической цепи от ёмкости конденсатора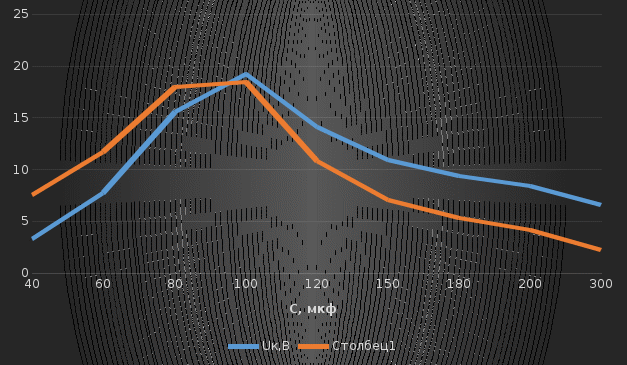



    Рис 2. – Зависимость напряжений на катушке и конденсаторе от ёмкости конденсатора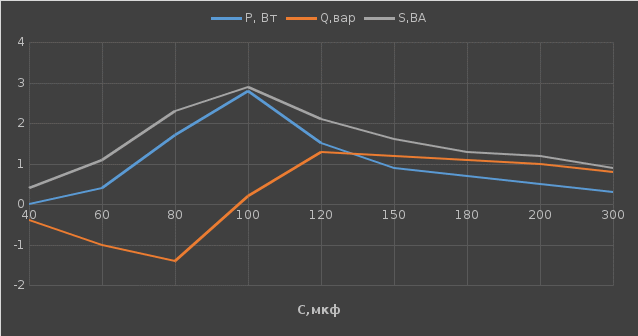



    Рис 3. – Зависимость активной P, реактивной Q и полной S мощностей от ёмкости конденсатора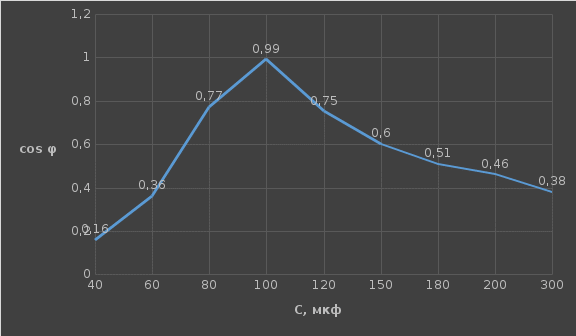


    Рис 4. – Зависимость коэффициента мощности cosφ от ёмкости конденсатора
    Проанализировав построенные графики зависимостей может заметить что рост измеряемых параметров заметен в промежутке от 40 мкФ до 100 мкФ, снижение в интервале от 100 до 300 мкФ, максимум измеряемых параметров наблюдается в точке соответствующей 100 мкФ. Для графика зависимости реактивной мощности Q от емкости конденсатора можно отметить, что в промежутке от 40 мкФ до 80 мкФ наблюдается уменьшение реактивной мощности, при 98 мкФ реактивная мощность стремится к нулю, далее в точке 120 мкФ достигает своего максимума, после чего уменьшается.

    Таким образом, можно сделать вывод, что для данной электрической цепи резонанс наступает при С=98 мкФ.

    1. Резонансный режим наступает в момент, когда реактивная мощность равна нулю, следовательно, когда XL = XC.

    2. По построенным в п.1 зависимостям напишите отличительные особенности резонансного режима электрической цепи.

    При работе электрической цепи в резонансном режиме наблюдается максимум таких параметров как сила тока в цепи, напряжение на катушке и конденсаторе, активная и полная мощность и коэффициент мощности cosφ, а реактивная мощность равна нулю.

    Также стоит отметить, что при резонансе напряжение на катушке и конденсаторе заметно выше, чем на клеммах цепи

    1. Построим векторную диаграмму напряжений для дальнейшей работы: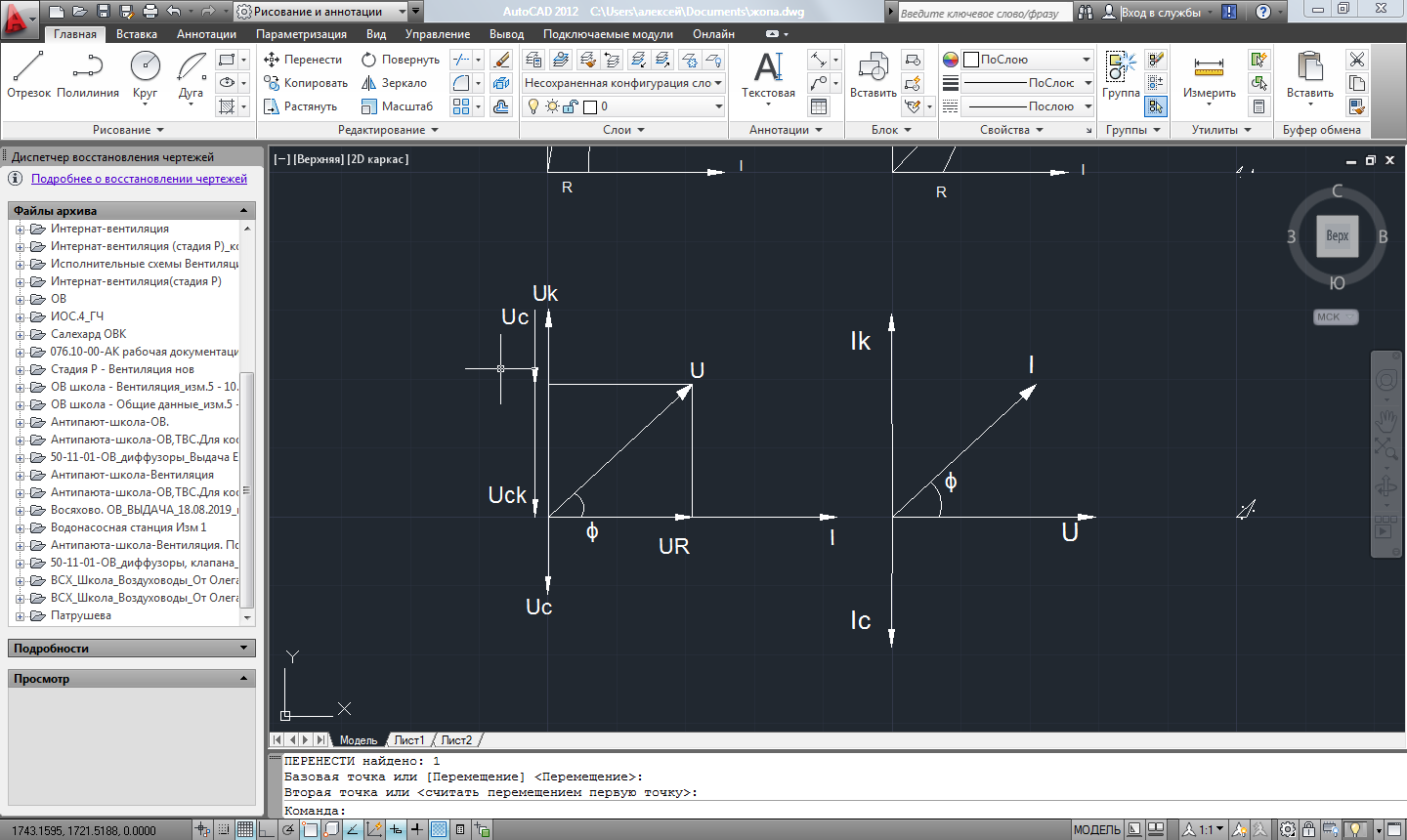



    Рисунок 5 – Векторная диаграмма напряжений
    В общем случае полное сопротивление электрической цепи синусоидального тока представляет собой комплексную величину Z с действительной частью R и мнимой частью jX: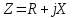



    R – эквивалентное активное сопротивление
    jX – эквивалентное реактивное сопротивление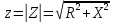



    Определим значения R,X и Z: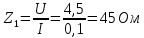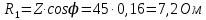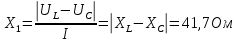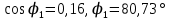






    Рисунок 6 –Треугольник сопротивления для первой строчки таблицы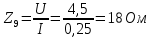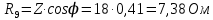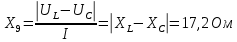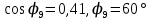







    Рисунок 7 –Треугольник сопротивления для девятой строчки таблицы
    Построим треугольники мощностей: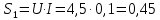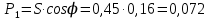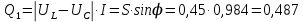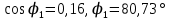







    Рисунок 8 –Треугольник мощностей для первой строчки таблицы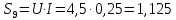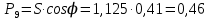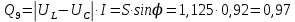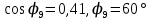







    Рисунок 9 –Треугольник мощностей для девятой строчки таблицы


    1. По векторной диаграмме проверим выполнение закона Кирхгофа для первой строчки в таблице:


    По векторной диаграмме (рис 5.) видно, что выполнение второго закона Кирхгофа соблюдается, если геометрически сложить вектора UR,UK и UC, получится вектор U: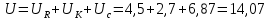



    1. Проверим по уравнению баланса мощностей первую строчку в таблице:


    Исходя из треугольника мощности наглядно видно, что векторная сумма активной и реактивной мощностей равна полной мощности, следовательно баланс мощностей соблюдается (рис.8)

    Опыт № 2. Параллельное соединение катушки индуктивности и конденсатора. Резонанс токов.



    N
    C, мкФ
    I, А
    IК, В
    IC, В
    P, Вт
    Q, вар
    S, ВА
    cos

    1
    40
    0,32
    0,38
    0,07
    1
    2,1
    2,4
    0,41

    2
    60
    0,29
    0,38
    0,1
    0,9
    1,8
    2,1
    0,45

    3
    80
    0,26
    0,38
    0,14
    0,9
    1,5
    1,9
    0,52

    4
    100
    0,23
    0,38
    0,18
    0,9
    1,2
    1,7
    0,59

    5
    120
    0,2
    0,38
    0,21
    0,9
    1
    1,5
    0,66

    6
    150
    0,18
    0,38
    0,24
    0,9
    0,8
    1,3
    0,76

    7
    180
    0,16
    0,38
    0,28
    0,9
    0,5
    1,2
    0,85

    8
    200
    0,14
    0,38
    0,31
    0,9
    0,3
    1,1
    0,94

    9
    300
    0,17
    0,38
    0,45
    1
    0,7
    1,2
    0,81




    1. Используя величины параметров таблицы 2 постройте и проанализируйте семейства зависимостей от емкости конденсатора:

    • токов генератора, катушки индуктивности и конденсатора;

    • активной, реактивной и полной мощностей

    • коэффициента мощности cosφ;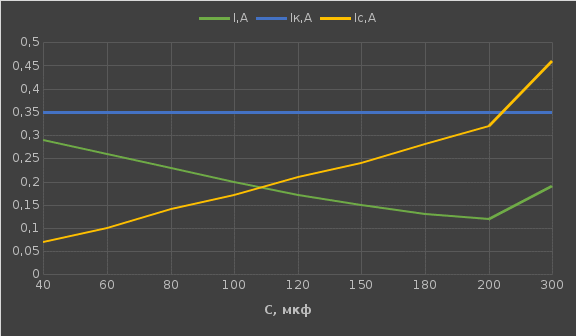





    Рис. 10 – Зависимость тока генератора, катушки и конденсатора от емкости конденсатора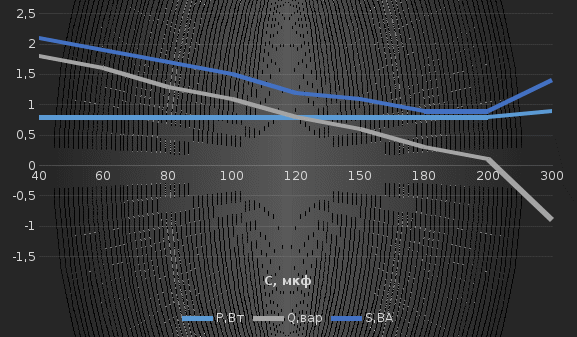



    Рис. 11 – Зависимость активной, реактивной и полной мощности от емкости конденсатора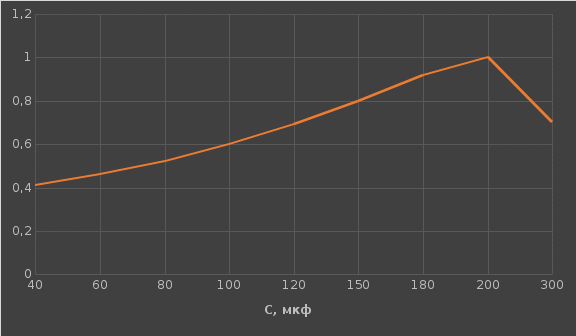



    Рис. 12 – Зависимость коэффициента мощности от емкости конденсатора

    Проанализировав построенные графики зависимостей, может заметить, что:

    • Сила тока на генераторе и полная мощность уменьшаются на всём интервале измерений (от 40 до 300 мкФ);

    • Коэффициент мощности растёт на всём участке (от 40 до 300 мкФ);

    • Сила тока на катушке остаётся неизменной, сила тока на конденсаторе растёт на протяжении всего интервала измерений;

    • Активная мощность также неизменна на всём интервале, реактивная же уменьшается на всём интервале измерений (от 40 до 300 мкФ);

    Исходя из чего можно сделать вывод, что резонанс наблюдается на максимуме коэффициента мощности и при нулевой реактивной мощности.

    8. Резонансный режим наступает в момент, когда cosφ = 1, т.е. реактивная мощность равна нулю, следовательно, когда XL = XC

    9. Главной отличительной особенностью является это то, что полная проводимость всей цепи равна активной проводимости, так же ток в неразветвлённой цепи и приложенное напряжение совпадают по фазе (ϕ=0°), ток в неразветвлённой части цепи достигает минимальное значение и равен активному току, токи в ветвях с индуктивностью и ёмкостью равны друг другу и противоположны по направлению.

    10.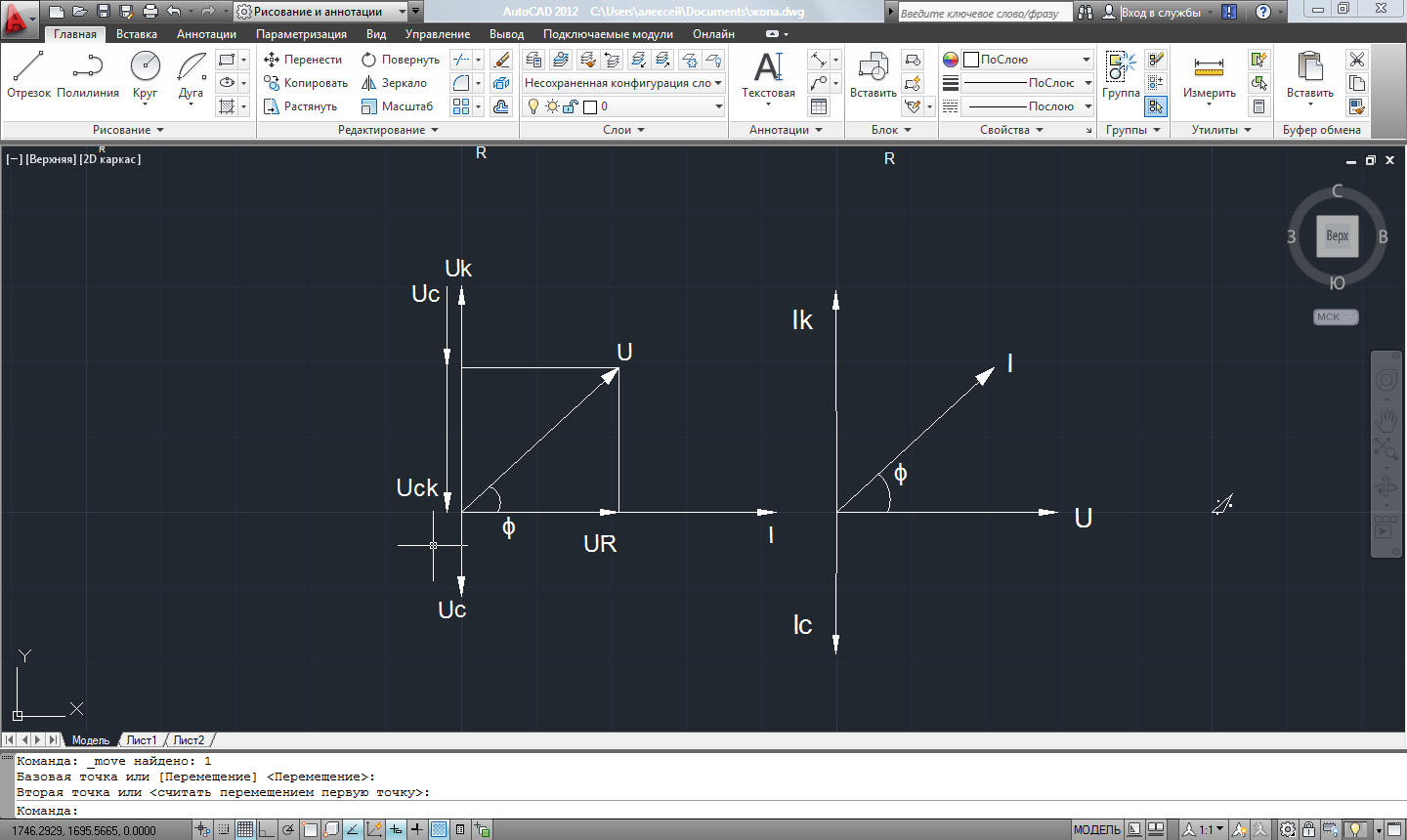



    Рисунок 13 – Векторная диаграмма токов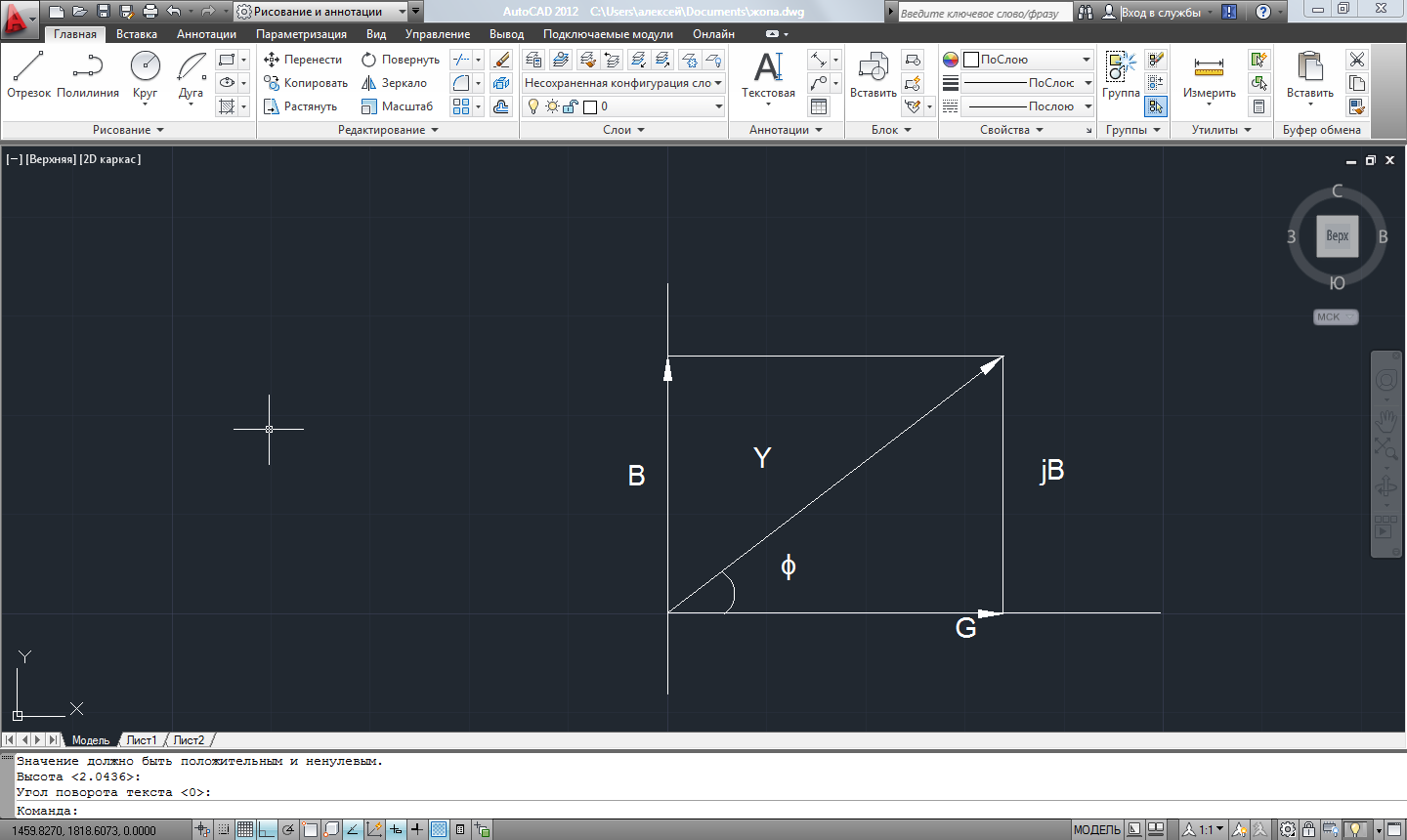



    Рисунок 14 – Векторная диаграмма проводимости

    Построим треугольники мощностей для первой строчки таблицы:

    P1=0,8В Q1=1,8В S1=2,1В ϕ=60° U=7,5Вт по таблице 2 стр.1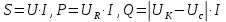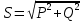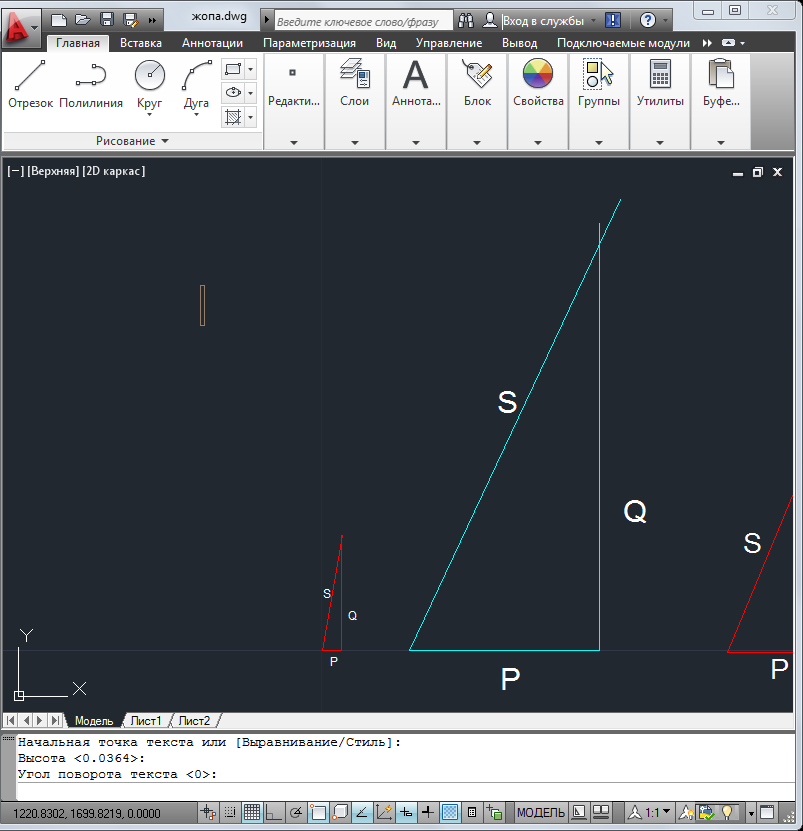





    Рисунок 15 – треугольник мощностей по первой строчке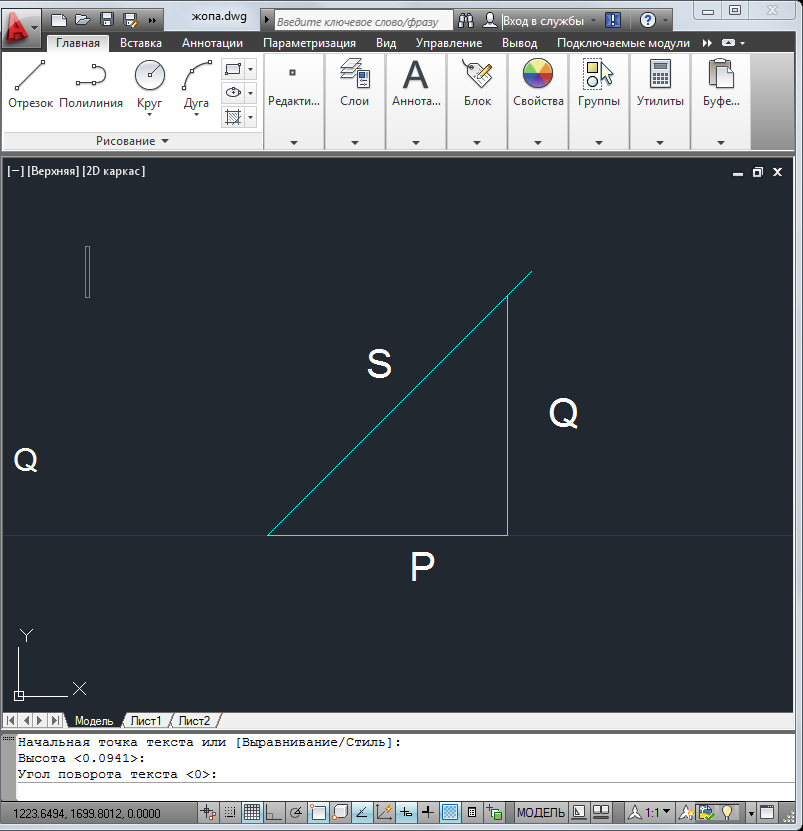


    Рисунок 16 – треугольник мощностей по девятой строчке
    S=2,4В P=1 В Q=2,1 ϕ=50°
    Треугольники проводимостей :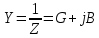



    G-действительная часть, активная составляющая
    B- мнимая часть, реактивная составляющая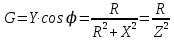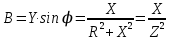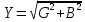



    Для первой строчки: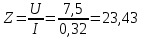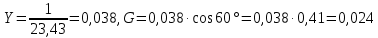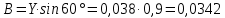






    Рисунок 17 – треугольник проводимостей по первой строчке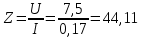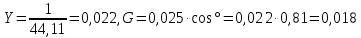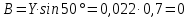



    ,0154


    Рисунок 18 – треугольник проводимостей по девятой строчке
    11. По векторной диаграмме проверим выполнение закона Кирхгофа для первой строчки в таблице:
    По векторной диаграмме (рис.13) наглядно видно, что первый закон Кирхгофа для мгновенных значений токов выполняется, так как сумма всех токов равна нулю
    12. Проверим по уравнению баланса мощностей первую строчку в таблице:
    Исходя из треугольника мощности наглядно видно, что векторная сумма активной и реактивной мощностей равна полной мощности, следовательно баланс мощностей соблюдается (рис.15)
    13. Вывод: Исследовали распределение токов, напряжений и мощностей при различных способах соединения катушки индуктивности и конденсатора. Определили условия наступления резонансного режима работы электрической цепи. Выявили особенности работы электрической цепи при резонансе. Экспериментально подтвердили законы Кирхгофа, закон Ома, баланс мощности для электрической цепи синусоидального тока.

    написать администратору сайта