лр3. 1 лр. Исследование разомкнутой линейной системы

• Название: Исследование разомкнутой линейной системы
• Дата: 13.11.2022
• Размер: 323 Kb.
• Имя файла: 1 лр.doc
• Тип: Исследование; #785878

Лабораторная работа №1

Тема: Исследование разомкнутой линейной системы

Вариант11



1.Описание системы

Исследуется система, описываемая математической моделью в виде передаточной функции

F(s)= 2 s^2 + 0.6 s - 0.36

---------------------------------

s^3 + 1.2 s^2 + 0.7406 s + 0.2734

2. Результаты исследования

-адрес файла tf.m:

C:\Program Files\MATLAB\R2009b\toolbox\control\control\@tf\tf.m % tf constructor

-нули передаточной функции

z =

-0.6000

0.3000

-полюса передаточной функции

p =

-0.7000

-0.2500 + 0.5728i

-0.2500 - 0.5728i

-коэффициент усиления звена в установившемся режиме

k =

-1.3168

-полоса пропускаемой системы

b = 2.2532

-модель системы в пространстве состояний

a =

x1 x2 x3

x1 -1.2 -0.7406 -0.5468

x2 1 0 0

x3 0 0.5 0

b =

u1

x1 2

x2 0

x3 0

c =

x1 x2 x3

y1 1 0.3 -0.36

d =

u1

y1 0

-статический коэффициент усиления после изменения матрицы D

k1 = -1.3168

Связь между к и к1 объясняется тем что…….

-модель в форме «нули-полюса»

2 (s+0.6) (s-0.3)

-----------------------------

(s+0.7) (s^2 + 0.5s + 0.3906)

-коэффициенты демпфирования и частоты среза

wc =

0.6250

0.6250

0.7000;

ksi =

0.4000

0.4000

1.0000;

p =

-0.2500 + 0.5728i

-0.2500 - 0.5728i

-0.7000 .

-импульсные характеристики получились одинаковые потому что……..

-переходные процессы исходной и модифицированной системы

-амплитудная частотная характеристика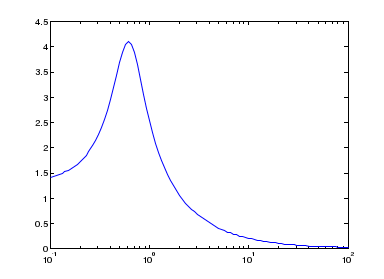



-для того ,чтобы найти статический коэффициент усиления по АХЧ, надо………..

- для того ,чтобы найти полосу пропускания по АХЧ,надо….

-реакция на сигнал, состоящий из прямоугольный импульсов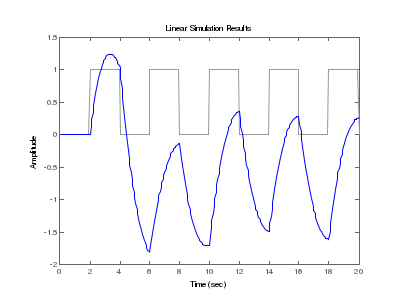



Лабораторная работа №2

Тема: Проектирование регулятора для линейной системы

Вариант 11

1. 
   Описание системы
   

Движение судна описывается линейной математической моделью в виде передаточной функции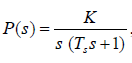

,где к=0,08рад/сек, Ts=18,0сек,

Привод моделируется как интегрирующее звено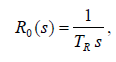

Tr=1сек,

Охваченное единичной отрицательной обратной связью. Модель измерительного устройства представляет собой апериодическое звено с передаточной функцией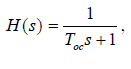

Tос=5сек

2. 
   Исследование разомкнутой системы
   

-Передаточная функция рулевого устройства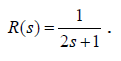



-Передаточная функция последовательного соединения объекта с приводом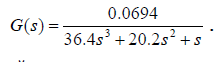



-ЛАФЧХ разомкнутой системы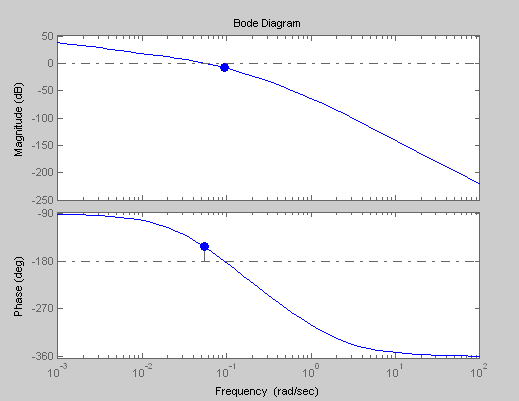

3. 
   Исследование системы с пропорциональным регулятором
   

-Переходная функция замкнутой системы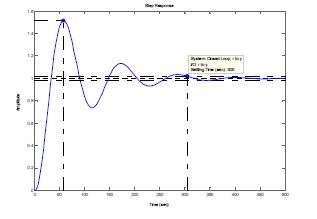



-Для обеспечения перерегулирования не более 10% требуется уменьшить коэффициент регулятора до значения C(s)= 0.33826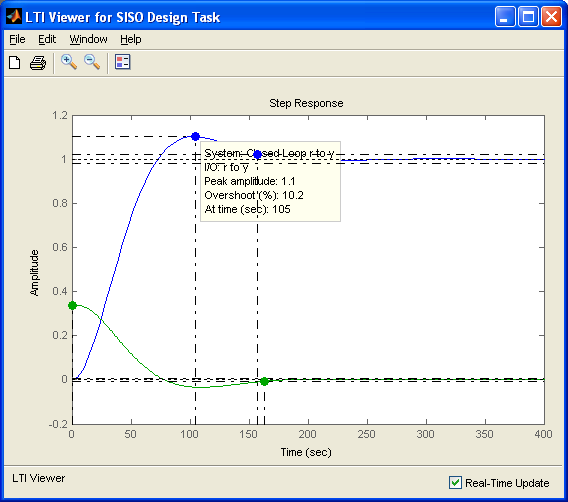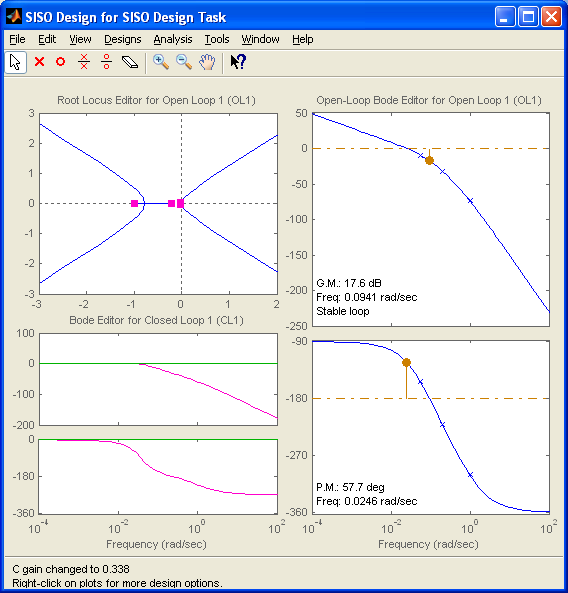





4. Исследование системы с пропорционально-дифференциальным(ПД-)

4.1 Регулятор ,обеспечивающий перерегулирование 10%

-Для обеспечения перерегулирования 10% требуется выбрать Кс=1.0578

-Переходная функция скорректированной замкнутой системы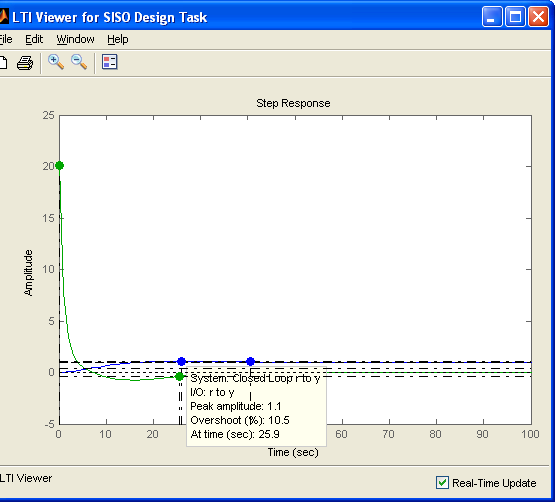



Дополнительный коэффициент усиления равен 1.0578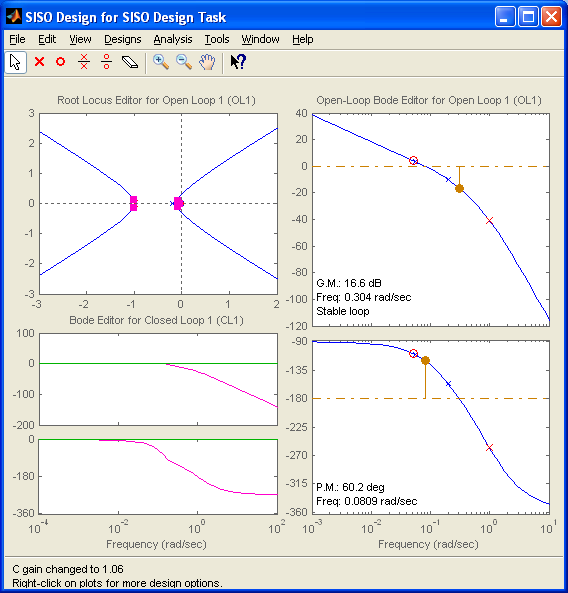



Время=25.9

Запасы устойчивости из графика = 16,6дБ, 60,2гр

4.2 Регулятор, обеспечивающий кратчайший переходный процесс

-Для обеспечения минимального времени переходного процесса требуется выбрать К=0,704Переходная функция скорректированной системы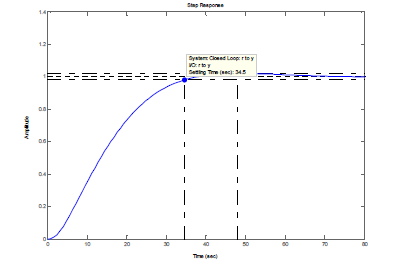

-Передаточная функция замкнутой системы

0.089327 s (s+0.05263) (s+0.05556) (s+0.2) (s+1)^2

--------------------------------------------------------------

s (s+1)^2 (s+0.05556) (s+0.05082) (s^2 + 0.1601s + 0.01737)

-Полюса передаточной функции

ans =

-1.0223 + 0.1425i

-1.0223 - 0.1425i

-0.0801 + 0.1047i

-0.0801 - 0.1047i

-0.0508

-Передаточная функция замкнутой системы от входа к сигналу управления

20.0986 s (s+0.05263) (s+0.05556) (s+0.2) (s+1)

------------------------------------------------------------

(s+0.05082) (s^2 + 0.1601s + 0.01737) (s^2 + 2.045s + 1.065)

-Изменение сигнала управления при единичном ступенчатом входном сигнале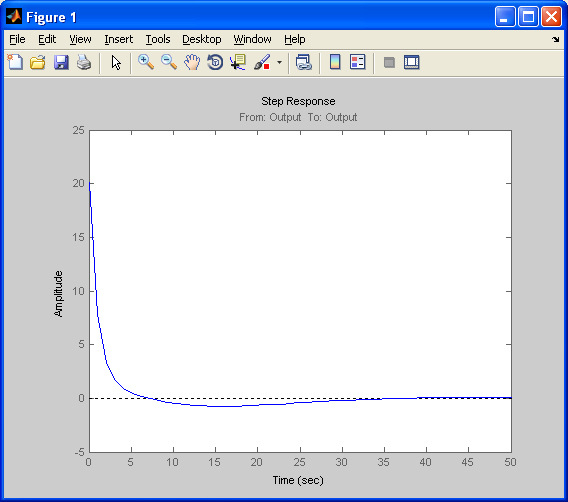



5. Код программы

1)p=tf(0.08,[18.0 1 0])

Transfer function:

0.08

----------

18 s^2 + s

2)R0=tf(1,[1 0])

Transfer function:

1

-

s

3) R=feedback(R0,1)

Transfer function:

1

-----

s + 1

4) G=p*R

Transfer function:

0.08

-------------------

18 s^3 + 19 s^2 + s

5) step(G)

6) H=tf(1,[5 1])

Transfer function:

1

-------

5 s + 1

7) L=G*H

Transfer function:

0.08

-----------------------------

90 s^4 + 113 s^3 + 24 s^2 + s

8) bode(L)

9)cpd=1+tf([18 0],[1 1])

Transfer function:

19 s + 1

--------

s + 1

10)w=c*G/(1+c*G*H)

Zero/pole/gain from input "Output" to output "Output":

0.089327 s (s+0.05263) (s+0.05556) (s+0.2) (s+1)^2

--------------------------------------------------------------

s (s+1)^2 (s+0.05556) (s+0.05082) (s^2 + 0.1601s + 0.01737) (s^2 + 2.045s + 1.065)

11) w=minreal(w)

Zero/pole/gain from input "Output" to output "Output":

0.089327 (s+0.05263) (s+0.2)

------------------------------------------------------------

(s+0.05082) (s^2 + 0.1601s + 0.01737) (s^2 + 2.045s + 1.065)

12)pole(w)

ans =

-1.0223 + 0.1425i

-1.0223 - 0.1425i

-0.0801 + 0.1047i

-0.0801 - 0.1047i

-0.0508

13)dcgain(w) ans =1.0000

14) Wu=minreal(c/(1+c*G*H))

Zero/pole/gain from input "Output" to output "Output":

20.0986 s (s+0.05263) (s+0.05556) (s+0.2) (s+1)

------------------------------------------------------------

(s+0.05082) (s^2 + 0.1601s + 0.01737) (s^2 + 2.045s + 1.065)

15) step(Wu)

Лабораторная работа №3

Тема: Моделирование систем управления в пакете Simulink

Вариант11

1. 
   Описание системы
   

Движение судна описывается линейной математической моделью в виде передаточной функции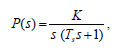

где К=0.08рад/сек,Ts=18,0сек,

Привод моделируется как интегрирующее звено,охваченное единичной орицательной обратной связью,так что его передаточная функция равна:

Tr=2сек

Измерительное устройство(гирокомпас) моделируется как апериодическое звено с переодичной функцией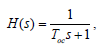

Tос=6сек,

2. 
   Исследование системы с ПД- регулятором
   

-передаточная функция ПД-регулятора, обеспечивающего переходный процесс минимальной длительности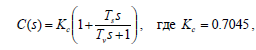



Ts=18.0 сек,Tv=1сек

-модель системы с ПД- регулятором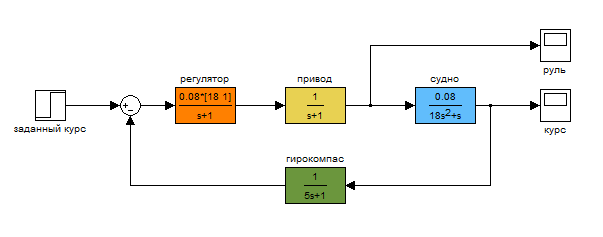



-переходные провесы в системе с ПД-регулятором при изменении курса на 10градусов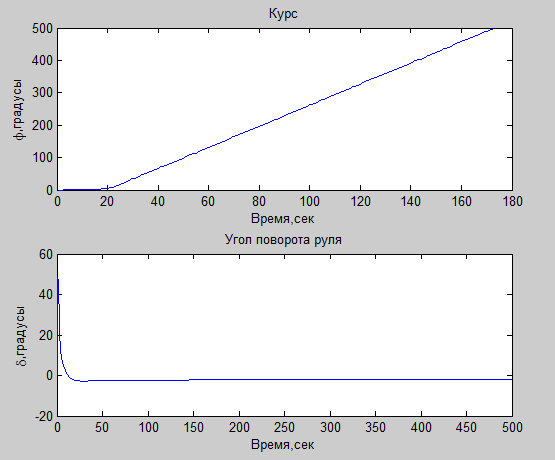



-модель системы с ПД- регулятором с учетом внешнего возмущения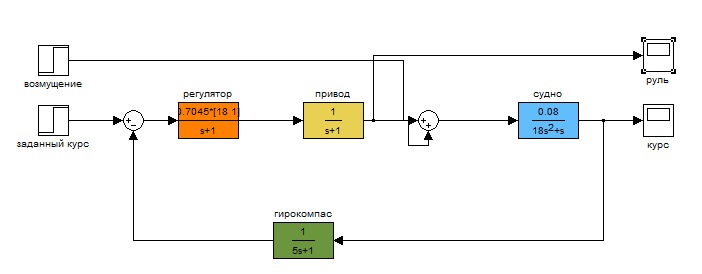



-передаточная функция по возмущению для системы с ПД- регулятором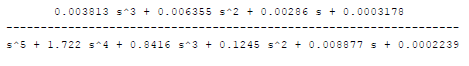



-судно с ПД- регулятором не вышло на заданный курс 10 градусов ,потому что

-статический киэеффициент усиления Кs=1,518,установившеесе значение сигнала выхода должно быть равно….,потому что;эти данные согласуются с результатами моделирования.

3. Исследование системы с ПИД-регулятором

-передаточная функция ПИД- регулятора

где Кс=0,7045,Тs=18.0сек,Tv=1cek,Tj=200cek,

-модель системы с ПИД- регулятором с учетом внешнего возмущения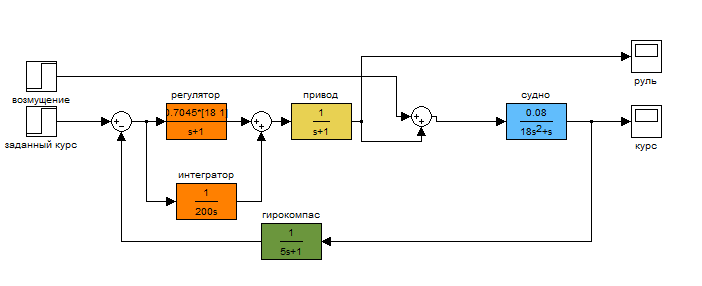



-передаточная функция по возмущению системы с ПИД- регулятором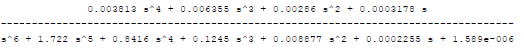



-при использовании ПИД-регулятора судно выходит за заданный курс,потому что…

-статический коэффициент Ks=…,установившееся значение сигнала выхода должно быть равно ….,потому что;эти данные согласуются с результатами моделирования

-переходные проуессы в системах с ПДи ПИД- регуляторами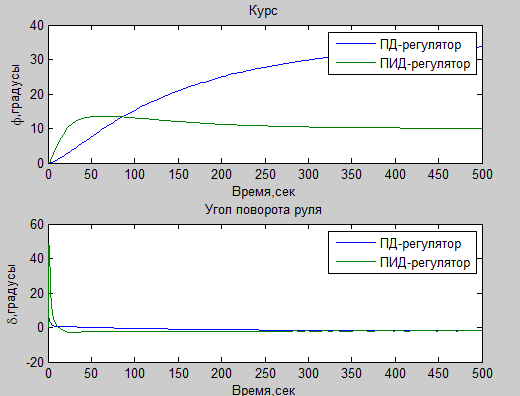



-при использовании ПИД-регулятора вместо ПД- регулятора ….

-при этом сигнал управления…

-в то же время(ухудшилось)

-передаточная функция разомкнутой системы с ПИД- регулятором рассчитывалась следующим образом

1)p=tf(0.08,[18 1 0])-передаточная функция модели судна

Transfer function:

0.08

----------

18 s^2 + s

2)R0=tf(1,[1 0])-передаточная функция интегрирующего звена

Transfer function:

1

-

s

3) R=feedback(R0,1)-передаточная функция рулевого устройства

Transfer function:

1

-----

s + 1

4) G=p*R –передаточная функция последовательного соединения объекта с приводом

Transfer function:

0.08

-------------------

18 s^3 + 19 s^2 + s

5) H=tf(1,[5 1])- передаточная функция измерительного устройства

Transfer function:

1

-------

5 s + 1

6) L=G*H-передаточная функция разомкнутого контура

Transfer function:

0.08

-----------------------------

90 s^4 + 113 s^3 + 24 s^2 + s

7) sisotool

8) cpd=1+tf([18 0],[1 1])- передаточная функция пропорционально-дифференциального(ПД)регулятора

Transfer function:

19 s + 1

--------

s + 1

9) w=c*G/(1+c*G*H)- передаточная функция полученной замкнутой системы.

0.084444 s (s+0.05263) (s+0.05556)(s+0.2) (s+1)^2

----------------------------------------

s (s+1)^2 (s+0.05556) (s+0.05065)(s^2 + 0.1625s + 0.01652)(s^2 + 2.042s + 1.062)

10) w=minreal(w)-минемальная реализация передаточной функции

0.084444 (s+0.05263) (s+0.2)

----------------------------------------

(s+0.05065) (s^2 + 0.1625s + 0.01652)(s^2 + 2.042s + 1.062)

11)wu=minreal(c/(1+c*G*H))- минимальная реализация передаточной функции замкнутой системы от входа к сигналу управления(выходу регулятора)

19 s (s+0.05263) (s+0.05556) (s+0.2) (s+1)

----------------------------------------

(s+0.05065) (s^2 + 0.1625s + 0.01652)(s^2 + 2.042s + 1.062)

-Запас устойчивости :

[gm,phim]=margin(w)

gm = 23.3962

phim = 123.2847

gm=20*log10(gm)

gm =27.3829

запасы являются достаточными.