Лабораторная работа №5 электродинамика лэти. ЛР5 ЭД. Исследование ширкополосного согласования сопротивления нагрузки и свчгенератора
 Скачать 444.15 Kb. Скачать 444.15 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра физической электроники и технологии отчет по лабораторной работе №5 по дисциплине «Электродинамика» Тема: ИССЛЕДОВАНИЕ ШИРКОПОЛОСНОГО СОГЛАСОВАНИЯ СОПРОТИВЛЕНИЯ НАГРУЗКИ И СВЧ-ГЕНЕРАТОРА
Санкт-Петербург 2017 Лабораторная работа №5 ИССЛЕДОВАНИЕ ШИРКОПОЛОСНОГО СОГЛАСОВАНИЯ СОПРОТИВЛЕНИЯ НАГРУЗКИ И СВЧ-ГЕНЕРАТОРА Цель работы. Расчет схемы согласующего тракта на основе микрополосковой линии передачи, обеспечивающего широкополосное согласование источника СВЧ-сигнала и нагрузки. Основные положения. Согласование сопротивлений является одной из важнейших задач техники СВЧ и заключается в обеспечении наиболее эффективной передачи сигнала из источника СВЧ-мощности в полезную нагрузку, в условиях, когда их сопротивления различны. Такое различие сопротивлений ведет к отражению части падающей мощности, и, следовательно, к снижению эффективности передачи. Задача согласования в общем случае может быть решена созданием согласующих схем на основе активных и реактивных сосредоточенных элементов, а применительно к СВЧ- на основе трансформаторов сопротивлений, разработанных с использованием теории длинных линий. Согласование нагрузки и подводящей линии передачи, имеющих сопротивления ZН и ZЛ соответственно, может быть выполнено с помощью λ/4 (четвертьволнового) трансформатора. Наиболее часто используемыми схемотехническими решениями при согласовании сопротивления нагрузки Zн с СВЧ-трактом являются согласующие линии с электрической длиной, равной λ/4 (одиночные или соединенные последовательно). Теоретический анализ распределенных линий основан на использовании телеграфных уравнений. Можно показать, что для линии передачи длиной l с волновым сопротивлением Z0, нагруженной на сопротивление Zн (рис. 1), справедлива формула трансформации сопротивлений: 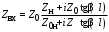 (1) (1)где β = 2π/λ – постоянная распространения.  Данное соотношение справедливо в случае отсутствия потерь в линии передачи. В ситуации, когда длина линии равна λ/4 (такая линия является трансформатором сопротивления) выражение (1) упрощается: 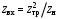 (2) (2)(Z0 переобозначили как Zтр). Тогда можем записать сопротивление трансформатора, путем замены Zвх на Zл: 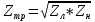 . (3) . (3)Для увеличения частотной полосы согласования применяют каскадное соединение трансформаторов (рис. 2). Теоретический анализ показывает, что при двухкаскадном соединении трансформаторов волновые сопротивления каждого из них могут быть определены, исходя из следующих соотношений: 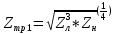 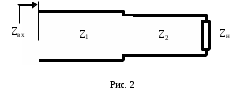 ; 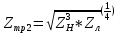 (4) (4)В интегральных схемах СВЧ используются планарные линии передачи, плоские проводники которых формируются на поверхности диэлектрической подложки методами интегральной технологии с применением фотолитографии для получения необходимого рисунка топологии. Наибольшее применение нашла микрополосковая линия (МПЛ), поперечное сечение которой представлено на рис. 3. МПЛ относится к категории линий со слоистым диэлектриком (диэлектрическая подложка – воздух), для которых вводится понятие эффективной диэлектрической проницаемости: 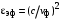 , где с – скорость света в свободном пространстве; vф – фазовая скорость волны в линии передачи. , где с – скорость света в свободном пространстве; vф – фазовая скорость волны в линии передачи. 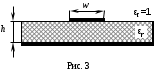 Введение 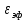 позволяет описывать рассматриваемую линию как некоторую эквивалентную, имеющую такие же геометрические размеры, но однородное диэлектрическое заполнение. В литературе приводится множество аналитических выражений для расчёта параметров МПЛ, полученных путём обработки результатов либо экспериментального исследования, либо численного моделирования на ЭВМ. Следует выделить две системы уравнений для расчёта параметров МПЛ необходимых для решения задачи согласования. В уравнения входят характеристическое сопротивление МПЛ Z0, ширина полоска w, толщина подложки h, диэлектрические проницаемости позволяет описывать рассматриваемую линию как некоторую эквивалентную, имеющую такие же геометрические размеры, но однородное диэлектрическое заполнение. В литературе приводится множество аналитических выражений для расчёта параметров МПЛ, полученных путём обработки результатов либо экспериментального исследования, либо численного моделирования на ЭВМ. Следует выделить две системы уравнений для расчёта параметров МПЛ необходимых для решения задачи согласования. В уравнения входят характеристическое сопротивление МПЛ Z0, ширина полоска w, толщина подложки h, диэлектрические проницаемости 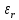 и и 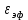 . Выражения (5) и (6) пригодны для расчёта при условии 0,05 < w/h <20, . Выражения (5) и (6) пригодны для расчёта при условии 0,05 < w/h <20, 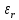 < 16; < 16;w/h < 1 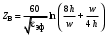 (5) (5)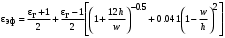 w/h  1 1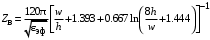 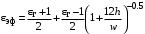 (6) (6)Полагая известными параметры диэлектрической подложки 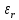 и h , а также требуемое значение Z0, рассчитанное для элементов трансформатора по выражениям (3) и (4), из систем (5) и (6) можно найти геометрические параметры трансформатора на основе МПЛ: ширину полоска w и длину отрезка и h , а также требуемое значение Z0, рассчитанное для элементов трансформатора по выражениям (3) и (4), из систем (5) и (6) можно найти геометрические параметры трансформатора на основе МПЛ: ширину полоска w и длину отрезка l = λ /4 , где λ = λ0/ 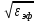 на частоте согласования. на частоте согласования.Выполнение работы. Рассчитаем одноэлементную и двухэлементную согласующую цепь Таблица 1- Данные к лабораторной работе
Для одноэлементной цепи волновое сопротивление трансформатора: Для двухэлементной согласующей цепи: 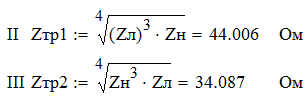 Решим системы уравнений 5 и 6 для определения длины и ширины отрезков МПЛ, составляющих трансформаторы. Для одноэлементной цепи:  Также, для подтверждения результата, определим ширину полоска графоаналитически: 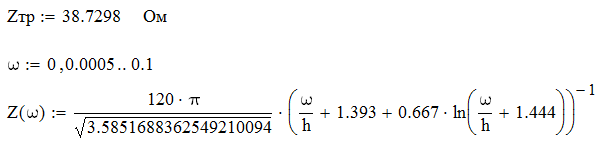 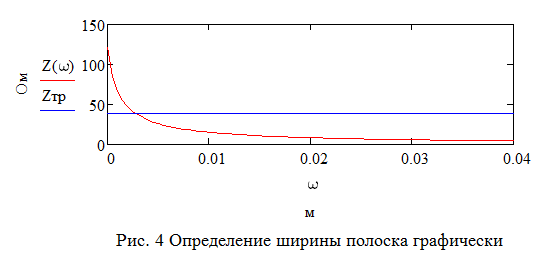 Значение почти совпало со значением, полученным при решении системы уравнений. Учитывая субъективную погрешность, можно утверждать, что ширина полоска определена верно. Для двухэлементной цепи: 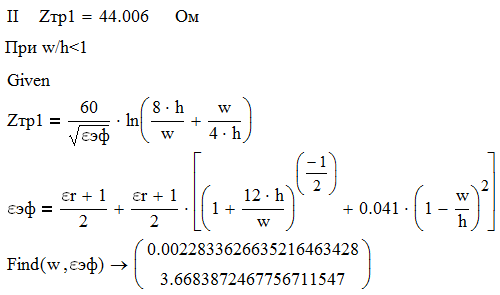 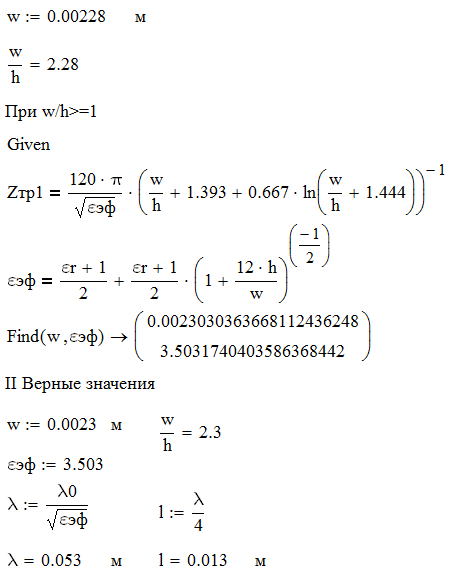 Определяем графоаналитически ширину полоска:  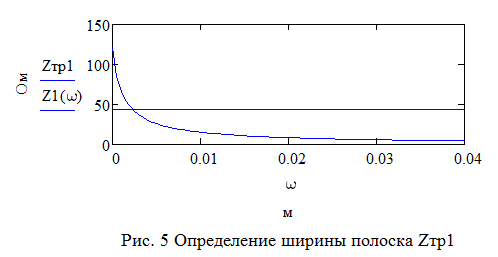 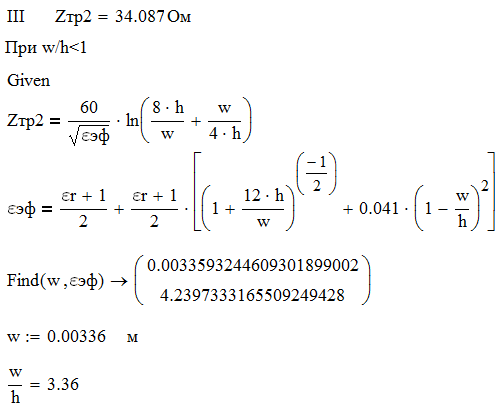 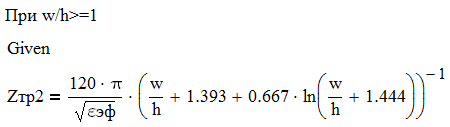  Ширина полоска графическим методом:  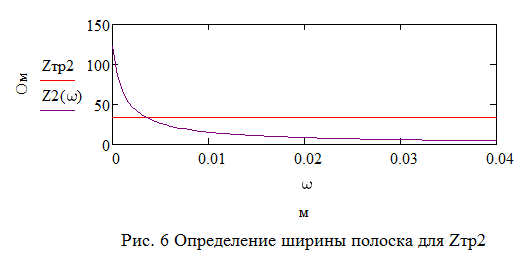 Учитывая, что в силу неточности визуального определения ширины полоска графоаналитически мы получаем некоторую погрешность, значения, полученные с помощью систем уравнений, положим истинными.  Проведем моделирование рассчитанных трансформаторов. Для одноэлементной цепи: 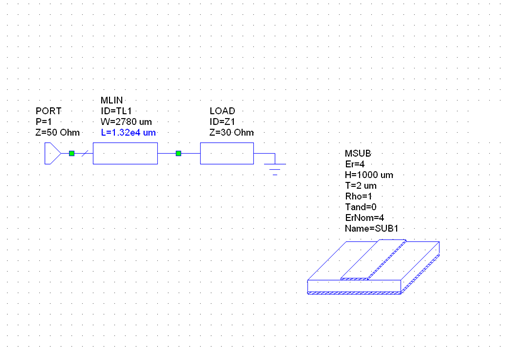 Рис. 7 Задание параметров одноэлементной цепи Пусть S- коэффициент отражения. Тогда получаем: 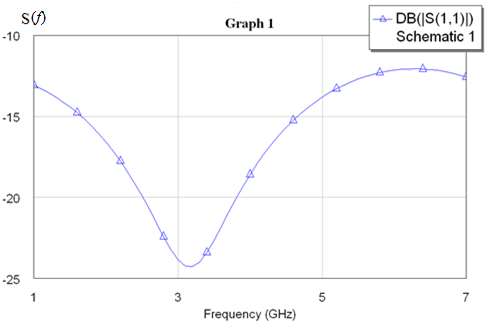 Рис. 8 Кривая коэффициента отражения для одноэлементной цепи Для двухэлементной цепи: 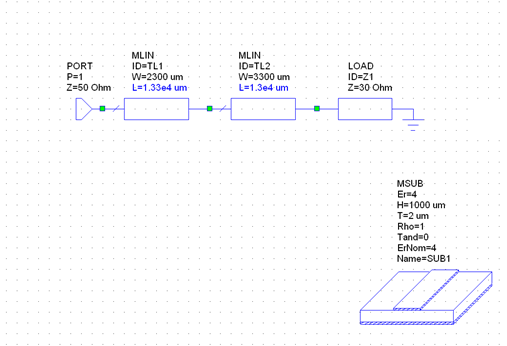 Рис. 9 Задание параметров двухэлементной цепи 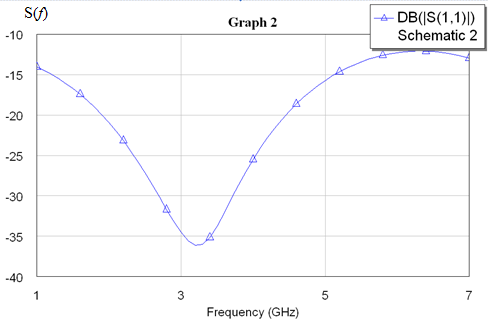 Рис. 10 Зависимость коэффициента отражения от частоты для двухэлементной цепи Построим график, который отобразит коэффициент отражения для двух типов цепей: 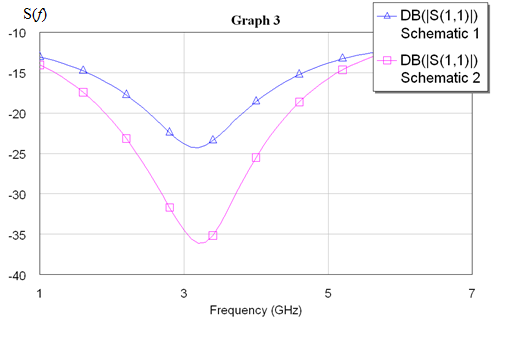 Рис. 11 Коэффициент отражения для одноэлементной и двухэлементной согласующих цепей Продемонстрируем диаграммы Смита для этих видов цепей: 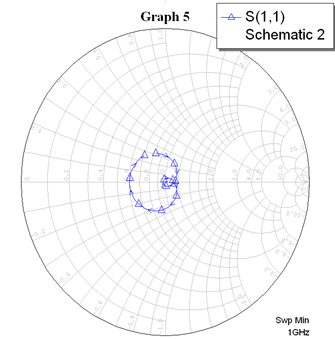 Рис. 12 Диаграмма Смита для одноэлементной цепи 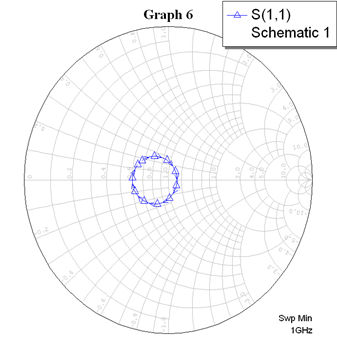 Рис. 13 Диаграмма Смита для двухэлементной цепи Вывод: В данной работе были рассчитаны геометрические параметры одноэлементной и двухэлементной цепи, основу которых составляют микрополосковые линии. Отличие одноэлементной линии от двухэлементной в том, что у двухэлементной линии коэффициент отражения менье, что мы можем наблюдать из рис. 11. |
