ўқитувчи. Продолжение табл (1). Исследование УпругоПластических Состояний Стержней при ПространственноПеременных Нагружениях
 Скачать 182.35 Kb. Скачать 182.35 Kb.
|
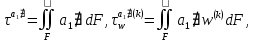 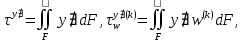 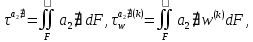 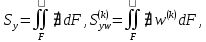 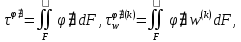 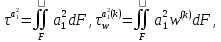 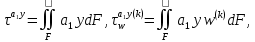 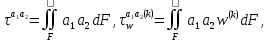 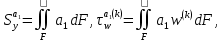 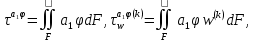 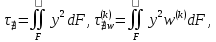 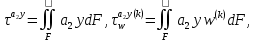 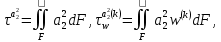 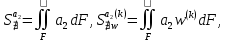 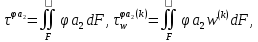 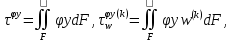 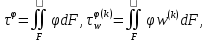 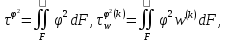 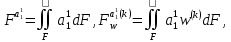 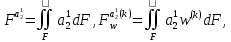 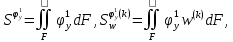 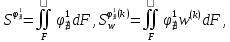 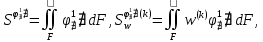 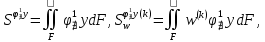 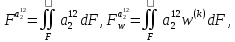 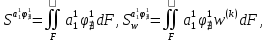 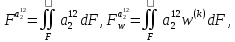 (I.I.15) (I.I.15)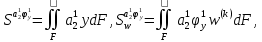 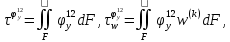 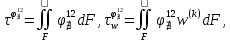 Теперь оформулируем вектор внутренних усилий: 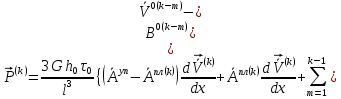 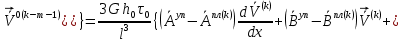 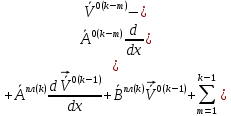 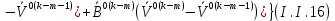 Здесь 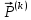 , , 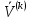 – вектор – функции двенадцатого порядка; – вектор – функции двенадцатого порядка;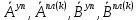 - квадратные матрицы двенадцатого порядка. - квадратные матрицы двенадцатого порядка.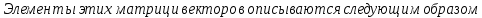 : : 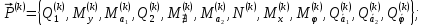 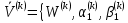 , , 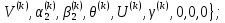 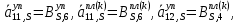 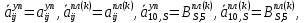 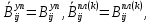 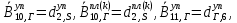 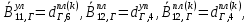 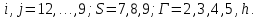 При построении (I.I.12), (I.I.13) и (I.I.16) были использованы безразмерные величины следующих видов: x= l 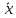 , y= , y=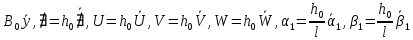 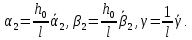 I.2. Решение краевых задач стержня методом конечных разностей Приведем построение вычислительной схемы для решения задачи (I.I.12), (I.I.13). Для этой используем центральные конечно-разностные соотношения [83] , аппроксимирующие производные с точностью до второго порядка в области 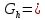 { {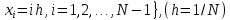 , ,тогда векторное уравнение (I.I.12) после аппроксимации получает вид 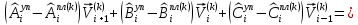 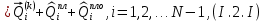 где 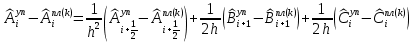 , , 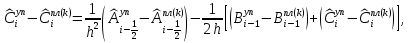 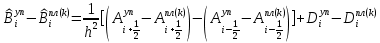 , ,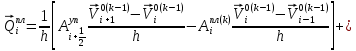 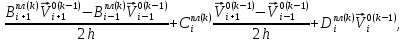 (I.2.2) 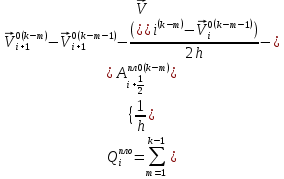 - 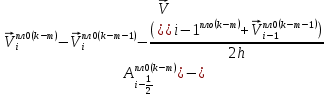 - 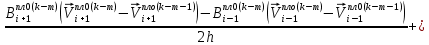 + 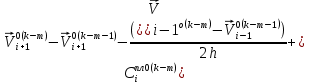 + 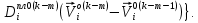 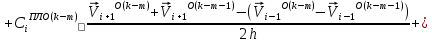 + 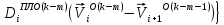 Теперь рассмотрим вопрос аппроксимации граничных условий. Если на границе задаются элементы вектора перемешения, тогда вариация вектора перемещения равняется нулю: 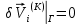 (1.2.3) (1.2.3)Если на торцах стержня задаются усилия, тогла выражения в фигурной скобке из граничных условий (1.2.3) должны равняться нулю: 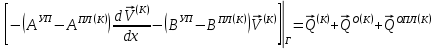 (1.2.4) (1.2.4)Здесь введено обозначение 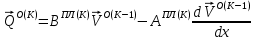 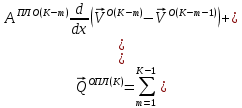 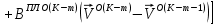 В свою очередь, граничные условия (1.2.3) и (1.2.4) можно обьединить в следующей форме: 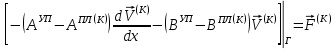 (1.2.5) (1.2.5)где 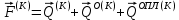 Соотношения (1.2.5) конкретизируем для частных случаев. Оба конца стержня жестко защемлены. ( 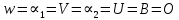 ) ) В данном случае 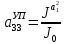 , , 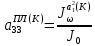 , , 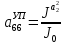 , , 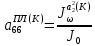 , ,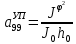 , , 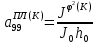 , , 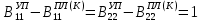 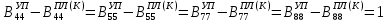 Остолные элементы матрицы 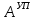 и и 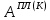 , а также , а также 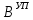 и и 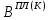 обращаются в нуль. Тогда формула (1.2.5) примет вид обращаются в нуль. Тогда формула (1.2.5) примет вид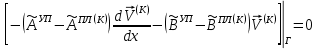 (1.2.6) (1.2.6)Оба конца стержня шарнирно закреплены (W=V=0). В этом случае формула (1.2.5) некоторые элементы матрицы и векторы принимают значения 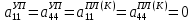 , , 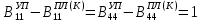 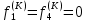 Соответотвующие видоизмененные матрицы и векторы обозначим двумя черточками. В результате получим: 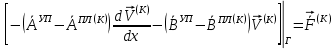 (1.2.7) (1.2.7)Если один конец стержня защемлен, а другой свободный, то формулы (1.2.5) найдем: для защемленного конца формируются формулы (1.2.6), а для свободного конца 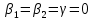 , некоторые элементы матрицы и вектора принимают значения: , некоторые элементы матрицы и вектора принимают значения: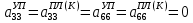 , , 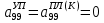 ; ;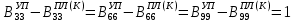 , , 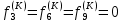 При этом на свободном конце стержня граничные условия (1.2.5) получают вид: 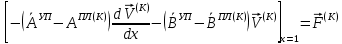 (1.2.8) (1.2.8)Аппроксимации граничных условий, т.е.е формул (1.2.6), (1.2.7), (1.2.8) имеют следующий вид: 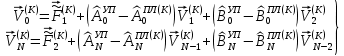 (1.2.9) (1.2.9)Где 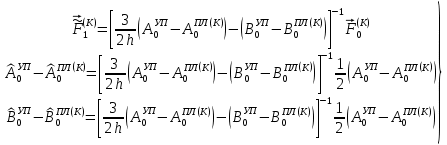 (1.2.10) (1.2.10)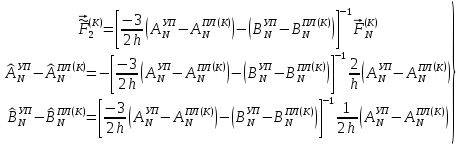 (1.2.11) Для решения сформулированных задач (1.2.1), (1.2.9) используем метод матричной прогонки, в котором на прямом ходе вычисляются прогоночные коэффициенты, а на обратном – находится решение системы алгебраических уравнений (14,83). Решение будем искать в виде 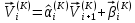 , , 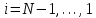 (1.2.12) (1.2.12)Где 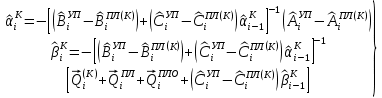 (1.2.13) (1.2.13)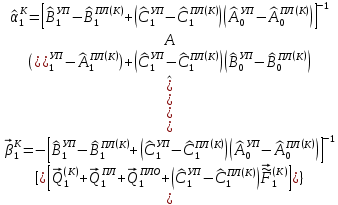 (1.2.14) (1.2.14)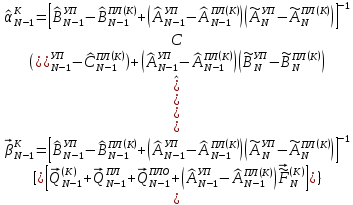 (1.2.15) (1.2.15)Для каждой нагрузки (К – число нагружий), формулу (1.2.12) повторяем до выполнения условия (это есть метод упругих решений А.А.Ильюшина) 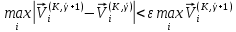 , (1.2.16) , (1.2.16)здес 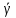 – число итерации, – число итерации, 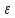 – точность вычисления. – точность вычисления.Опредилив векторы перемещений 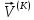 , вычисляем ынутренние усилия стержня (1.1.16). После аппроксимации вектор внутренних усилий принимает вид , вычисляем ынутренние усилия стержня (1.1.16). После аппроксимации вектор внутренних усилий принимает вид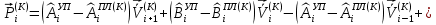 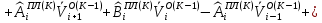 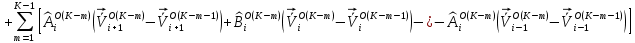 (1.2.17) где 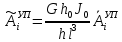 , , 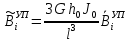 , ,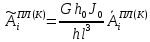 , , 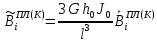 1.3. Разработка комплекса программ для решения краевых задач стержня при пространственнопеременном нагружении На основе приведенных выше алгоритмов разрабатывается комплекс програм, с помощью которых определяются параметры в сечениях стержня, показывающие появление пластических точек. Точки фиксируются и на их основе вычисляются распределения функции Ильюшина и определяются пластические зоны. Далее, с учетом функции пластичности на основе приближенного интегрирования вычисляются характеристики сечения стержня  и заново решается система алгебраических уравнений. и заново решается система алгебраических уравнений.Переменние упруго-пластические нагружения играют существенную роль, потому что в процессе каждого нагружения решается более трудная задача, нежели при предыдущем упруго-пластическом нагружении. Поэтому в памяли ЭВМ хранится большой объём информации о предыдущих полуциклах. Структура и комплекс программ отражены в виде блок-схемы (рис 1.3.1) Блоком 1 подготоавливаются стандартные программы (для обрашения матриц, их умножения и т.д.) из библиотеки стандартных програм. Этим же блоком аписываются все параметры и формируются процедуры приближенного интогрирования и вычисления внутренних усилий. Блоком 2 вводится исходная информация геометрические и механические характеристики стержня ( 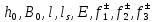 ); количество уравноний ( ); количество уравноний (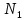 ); число узлов сетки (N); количество ограничений нагружения (К) и точность вычислений итерационного процесса ); число узлов сетки (N); количество ограничений нагружения (К) и точность вычислений итерационного процесса 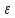 . Блоком 3 формируются упругие коэффициенты, свободные члены векторного дифференциального уравнения (1.1.12) и граничные условия (1.1.13), ( . Блоком 3 формируются упругие коэффициенты, свободные члены векторного дифференциального уравнения (1.1.12) и граничные условия (1.1.13), (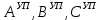 , , 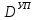 и F, и F, 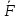 ). Этим же блоком идентификатору цикла нагружения К и цикла итерации ). Этим же блоком идентификатору цикла нагружения К и цикла итерации 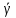 присваивается значение нуль. присваивается значение нуль.Таким образом, формируются упругие коэффициенты дифференциального уравнения (1.1.12). Блоком 4 вычисляет коэффициенты системы алгебраических уравнений (1.2.1) на основе метода конечных разностей ( 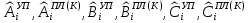 ), а блок 5 – прогоночнқе коэффициенты ), а блок 5 – прогоночнқе коэффициенты 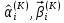 по формуле (1.2.13). Блоком 6 для каждого значения узла сетки N вычисляются компоненты искомых векторов по формуле (1.2.13). Блоком 6 для каждого значения узла сетки N вычисляются компоненты искомых векторов 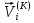 по формуле (1.2.12). При этом получаем упругие решения системы уравнений (1.2.1) с соосветствующими граничными условиями (1.2.10). Условия упругих решений проверяются (блок 7) и управления передаётся блоку 9, которым по формуле (1.2.17) вычисляются компоненты вектора внутренних усилий стержня по формуле (1.2.12). При этом получаем упругие решения системы уравнений (1.2.1) с соосветствующими граничными условиями (1.2.10). Условия упругих решений проверяются (блок 7) и управления передаётся блоку 9, которым по формуле (1.2.17) вычисляются компоненты вектора внутренних усилий стержня 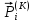 . На этом процесс решения упругих задач заканчивается. Полученные результаты печатаются блоком 10. . На этом процесс решения упругих задач заканчивается. Полученные результаты печатаются блоком 10.Дале проверяются упруго-пластические состояния стержня, блок 11 увеличивает число нагружений на единицу. Блок 12 проверяет цикл нагружения. Если цикс не закончен, то управление передаётся блоку 13. Если 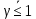 , то управления передаётся блоку 16, который начинает цикл по длине стержня (просматриваются все сечения с шагом h по длине стержня). Блоком 17 число итераций опять увеличивается на единицу, а в следующем блоке по формулам (1.1.2) и (1.1.6) вычисляются компоненты тензора деформаций ( , то управления передаётся блоку 16, который начинает цикл по длине стержня (просматриваются все сечения с шагом h по длине стержня). Блоком 17 число итераций опять увеличивается на единицу, а в следующем блоке по формулам (1.1.2) и (1.1.6) вычисляются компоненты тензора деформаций (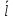 ) и интенсивность деформации ( ) и интенсивность деформации (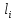 ) для фиксированного значения ) для фиксированного значения 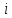 относительно текуўего сечения стержня. Вычисление отношения интенсивности деформации к деформации текучести относительно текуўего сечения стержня. Вычисление отношения интенсивности деформации к деформации текучести 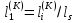 производится блоком 19 при К=1, производится блоком 19 при К=1, 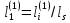 при при 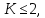 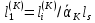 . Если условия блока 19 выполняется, то управление передаётся блоку 20. В противном случае значение . Если условия блока 19 выполняется, то управление передаётся блоку 20. В противном случае значение  увеличивается на единицу и управление передаётся блоку 18. Далее цикл повторяется. Если условия блока 19 выполнено, то управление увеличивается на единицу и управление передаётся блоку 18. Далее цикл повторяется. Если условия блока 19 выполнено, то управление                        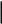  1 Передаётся блоку 20. Блок 20 по формуле (1.1.5) вычисляет значение функции пластичности. Далее для вычисления интегралов по формуле (1.1.15) производится обращение к интегральной процедуре Гаусса. Полученные значения сохраняются в массивах. Блок 20 проверяет условие окончания цикла по длине стержня. Если оно выполнию то управление передаётся блоку 23, который формирует упруго-пластические коэффициенты системы дифференциальных уравнений второго порядка (1.1.12) и граничные условия (1.1.13): 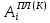 , , 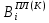 , , 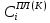 , , 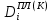 Далее управление передаётся блоку 4, где описанный процесс повторяется для упруго-пластического случая. При переходе к блоку 8 проверяется точность итерационного процесса по формуле (1.2.16). Выполнение условия блока 8 означает, что упруго-пластическое решение стержня получено с точностью 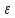 , а управление передаётся в 9-й блок. В противном случае – в блок 16 и процесс повторяется. Блок 9 по формуле (1.2.17) вычисляет компоненты вектора внутреннего усилия , а управление передаётся в 9-й блок. В противном случае – в блок 16 и процесс повторяется. Блок 9 по формуле (1.2.17) вычисляет компоненты вектора внутреннего усилия 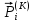 . На этом решение упруго-пластической задачи заканчивается. Полученные результаты выдаются на печать блоком 10. После этого решается упруго-пластическая задача при переменном нагружении. Блоком 12 сравнивается цикл нагружения К с ограничением КК1. Если это условия выполнено, то управление передаётся блоку 13. Так как . На этом решение упруго-пластической задачи заканчивается. Полученные результаты выдаются на печать блоком 10. После этого решается упруго-пластическая задача при переменном нагружении. Блоком 12 сравнивается цикл нагружения К с ограничением КК1. Если это условия выполнено, то управление передаётся блоку 13. Так как 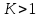 , осуществляется переход к блоку 14, где значение числа итерации , осуществляется переход к блоку 14, где значение числа итерации 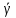 равняется нулю. При каждом нагружении стержня блоком 15 формируются векторы внешних нагрузок равняется нулю. При каждом нагружении стержня блоком 15 формируются векторы внешних нагрузок 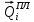 , , 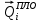 . Последние вқчисляются по формулам (1.2.2) и управление передаётся блоку 16. Далее этот процесс повторяется. Усли условия в блоке 12 не вқполняется, то работа программқ завершается и управление передаётся блоку 24. Таким образом, получаем численное упруго-пластическое решение стержня . Последние вқчисляются по формулам (1.2.2) и управление передаётся блоку 16. Далее этот процесс повторяется. Усли условия в блоке 12 не вқполняется, то работа программқ завершается и управление передаётся блоку 24. Таким образом, получаем численное упруго-пластическое решение стержня |
