ўқитувчи. Продолжение табл (1). Исследование УпругоПластических Состояний Стержней при ПространственноПеременных Нагружениях
 Скачать 182.35 Kb. Скачать 182.35 Kb.
|
|
Академия Наук Узбекской СССР Ордена Трудового Красного Знамени Институт Кибернетики С ВЧ НПО “ Кибернетика” АН Уз СССР На правах рукописи Олимов Муродилла УДК 539.374:621.743.4 Исследование Упруго-Пластических Состояний Стержней при Пространственно-Переменных Нагружениях 01.02.04 –механика деформируемого твердого тела Диссертация На соискание ученой степени кандидата физико-математических наук Научный руководитель-кандидат Технических наук Т.Юлдашев Ташкент-1985 Оглавление Стр. ВВЕДЕНИЕ ……………………………………………………………………………………………………………………………..4 ГЛАВА I.Разработка Алгоритмов Решения Статических Задач Стержней При Пространственно-Переменных Упруго-Пластических Нагружениях……………………………………16 I.1.Постановка краевой задачи …………………………………………………………………………………………16 I.2.Решение краевых задач стержня методом конечных разностей…………………………………29 I.3. Разработка комплекса программ для решения краевых задач стержня при пространственно-переменном нагружении……………………………………………………………………37 ГЛАВА II.Упруго-пластический расчет стержней при плоском и пространственном нагружениях…………………………………………………………………………………………………………………………43 2.1.Сравнительный анализ балок при чистом изгибе и при изгибе с учетом сдвига……..43 2.2.Исследование численной сходимости метода конечных разностей и напряженно-деформированного состояния упругого стержня при пространственном нагружении.46 2.3.Исследование численной сходимости метода конечных разностей,итерационного процесса и напряженно-деформированного состояния упруго-пластических стержней при изгибе и пространственном нагружении …………………………………………………………………………..58 2.3.1. Упруго-пластический изгиб защемленной с обоих концов балки при равномерно распределенной нагружении с учетом поперечного сдвига ……………………………………………58 2.3.2.Упруго-пластический изгиб шарнирно-опертой с обоих концов балки при равномерно распределенной нагрузке……………………………………………………………………………….68 2.3.3.Исследование напряженно-деформированного состояния защемленного на одном конце нагруженного на другом конце стержня …………………………………………………………………75 Глава III.Упруго-пластический расчет стержней при пространственно-переменном нагружении……………………………………………………………………………………………………………………………86 3.I.Исследование численной сходимости метода конечных разностей для расчета защемленного с обоих концов стержня при знакопеременном нагружении………………….86 3.2.Исследование упруго-пластического состояния стержней при пространственном нагружении с учетом нагрузки…………………………………………………………………………………………….98 3.3. Исследование упруго-пластического состояния защемленного с обоих концов стержня при пространственно-переменном нагружении …………………………………………………………106 Заключение……………………………………………………………………………………………..............................122 Список литературы……………………………………………………………………………………………………………124 Приложения ………………………………………………………………………………………………………………………134 ВВЕДЕНИЕ Многие вопросы,связанны с расчетом отдельных элементов конструкций,сводятся к исследованию напряженно-деформированного состояния стержня в пределах и за пределом упругости.Большинство технических задач,возникающих при констуировании машини проектировании сооружений,требует определения прочности и жесткости стержней,таких как кручение,растяжение,сжатие. Решение этой задачи посвящены известные монографии Х.Н.Арутюняна и В.П.Абрамяна [6],В.З.Власова [18,19],Г.Ю.Джанелидзе, Я.Г.Пановко [33], А.Н.Динника [30], Н.И.Мусхелишвили [72], Б.Сен-Венана [84] и многочисленные работы других авторов. При построении прикладной теории упругих стержней переход от исследования трехмерного тела к одномерному имеет решающее значение.Полное решение этой задачи получено на основе дискретно-континуального метода,разработанного В.З.Власовым [18]. Построение единой теории тонких и тонкостенных стержней было предложено в работах Г.Ю.Джанелидзе [31-33].Потребности практики приводят в настоящее время к необходимости изучения деформации элементов за пределами упругости.Исследованию напряженно-деформированного состояния упруго-пластических,идеально-пластических и жестко-пластических тел посвящены работы Д.Л.Быкова [17] ,М.П.Галина [21.22] ,А.А.Ильюшина [39-41],А.И.Ишлинского [44],Д.Д.Ивлева [38] ,В.К.Кабулова [46-48],Л.М.Качанова [51],И.А .Кийко[52],В.Д.Клюшникова[53],В.С.Ленского [61],В.В.Москвитина [65-69],Н.Н.Малинина [64],П.М.Огибалова [43],Б.Е.Победри [77],Ю.Н.Работнова [78],А.Р.Ржаницына [81],В.В.Соколовского[87],Г.С.Шапиро[93] и много других. Развитие современной техники и промышленного строительства ставит повышенные требования к расчету на прочность и деформируемость конструкций,состоящий из балок и стержней.В прикладных задачах видное место занимают упругое и упруго-пластическое равновесия стержней.Важный класс задач,когда внешние нагрузки являются пространственно-переменными,возникает в инженерной практике.При этом изменение свойств конструкций и материалов существенно отличается от случая одгократного нагружения.Специфические качество материалов,появляющихся при переменных нагрузках,являются основными факторами,определяющими прочность и долговечность целого ряда конструкций.В связи с повышенными требованиями,предъявляемыми к инженерным конструкциям,несущим элементами которых приходится работать при переменных нагрузках,возникает необходимость расчета напряженного и деформированного состояний с учетом физической нелинейности материало. Наряду с обширными исследованиями упруго-пластических деформаций твердого тела,находящегося под действием нагрузок,имеются работы,посвященные вопросам переменного деформирования упруго-пластических тел.Различные аспекты этой проблемы отражены в трудах Р.А.Арутюняна и А.А.Вакуленко [7],И.Б.Биргера [10],Т.Буриева [12-16],В.Д.Гаджиева[23-24],А.П.Гусенкова[26-27],А.А.Ильюшина[39-42],Ю.И.Кадашевича и В.В.Новожилова [49],В.В.Колокольчикова [55-57],В.В.Москвитина [65-69],С.В.Серенсена [85],Ю.Н.Шевченко [94-95],Р.М.Шнейдеровича [96-97] и ряда других авторов. Теория упругих упруго-пластических стержней привлекает к себе внимание многих исследователей.Предлагаются как новые теории стержней,так и новые трактовки известных теорий.Причиной этого является необходимость совершенствования методов расчета конструкций на прочность и жесткость. Возрастают требования к точности инженерных расчетов и расширяется круг явлений,подлежащих исследованию инженерными методами.Всякая теория стержней (ТС) приближенно описывает процессы в стержней и поэтому актуальными становятся вопросы о погрешностях той или иной ТС,о границах ее примености. Приведем анализ некоторых работ,посвященных построению теории и расчета стержней при упругих и упруго-пластических пространственных нагружениях и разгружениях.Большой теоретический и экспериментальный материал свидетельствует о серьезных успехах в развитии теории расчета упругого и упруго-пластического равновесия тонкостенных стержней.Эти успехи,главным образом,относятся к работам следующих ученых:В.З.Власова [18],А.А.Уманского,Р.А.Ададурова ,Г.Ю.Дженелидзе [31] и др. Среди классических задач определения напряженного состояния упругих тел при различных нагрузках важное место занимает задача кручения полых и составных упругих призматического стержня,основанное на гипотезе плоских сечений,принадлежит Кулону. В 1827 г.Коши,опираясь на введенные им общие уравнения теории упругости,исследовал вопросы кручения призматических стержней некруглого ( прямоугольного и квадратного) сечения.Несмотря на то,что решение носило приближенный характер,Коши теоретически доказал,что поперечное сечение стержня при круччении,вообще говоря,не остается плоским ( депланируется) [84]. Основываясь,на эти работы,В.Сен-Венан позднее дал строгую математическую модель кручения и изгиба призматических тел.Первая его работа,изданная в 1939 г.,содержала решение задачи о кручении прямоугольной призмы.Через несколько лет Сен-Венан дал общие уравнения этой теории.Он ввел так называемую функцию кручения 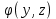 ,гармоническую в области поперечного сечения и показал,что задача кручения призматического бруса произвольного поперечного сечения сводится к определению этой функции. ,гармоническую в области поперечного сечения и показал,что задача кручения призматического бруса произвольного поперечного сечения сводится к определению этой функции.В работе [105] на основе известных вариационных принципов исследуются большие деформации стежней.Получены основные соотношения и уравнения,а также решены две задачи: о деформировании консольно-закрепленного тонкого гибкого стержня под действием концевого изгибающего момента и задача о прогиба защемленной по концом балки под действием сосредоточенной силы и распределенного момента.Полученные результаты сравнивались с экспериментальными данными.В статье [91] приводится метод построения пространственных форм равновесия упругих стержней,деформированных концевыми нагрузками,основанный на уравнениях Е.Л.Николаи,а также исследуются новые уравнения,определяющие закручивание стержней вдоль упругой линии и позволяющие наглядно изобразить все особенности сооветствующего равновесия. В работе [104] описывается теория В.З.Власова,применяемая для тонкостенных призматических стержней с многозамкнутым конкурсом поперечного сечения.Исходные соотношения теории тонкостенных стержней записываются в полярных координатах с учетом деформации контура сечения.В качестве примера рассматривается изгиб плоскости консольной части кольца с тонкостенным сечением в форме прямоугольника,причем задаваемые функции отражают осевое растяжения,закон плоских сечений при изгибе в других плоскостях и депланацию сечения при кручении. В работе Ж.Н.Дмитриевой [34] исследуется система уравнений типа Тимошенко,которая дополнена нелинейными членами,учитывающими цепные напряжения.При этих предположениях из исходной системы получены два связанных обыкновенных дифференциальных уравнения одно из которых содержит нелинейный член (кубическую степень функции).В эти уравнения добавлены также члены с производными по времени,учитывающие вязкие затухающие колебания.В работе [60] Б.Б.Лампоси приводится уравнения и полностью решается задача определения напряжения в случае изгиба в двух плоскостях и кручения (в том числе и стесненного) для достаточного произвольного по форме поперечного сечения.В этой же главе описываются формулы в замкнутой виде для координат центра изгиба стержней с замкнутым поперечным сечением.Показано,что случай открытого профиля может рассматриваться как частный случай двухсвязанных поперечных сечений. В работе [2] для прямолинейных тонкостенных стержней при наличии упругих связей получены выражения частот изгибно-крутильных колебаний и критического момента в задаче устойчивости и плоской формы изгиба. Т.Р.Рашидовым и его учениками [79] исследовано колебание подземных сооружений при сейсмических воздействиях ;при этом подземные сооружения рассматриваются как сложная система ,состоящая из системы трубопроводов и сооружений ,стыкуемых в сложных узлах различным образом.Удлиненные,стыкуемые между собой участки рассматриваются как брусья (балки) ,работающие на растяжение-сжатие,изгиб и кручение и взаимодействующие с узловыми сооружениями. В работах [21,87] для решения упруго-пластического кручения призматических стержней предложены полуобратные методы,а именно: заранее заданы некоторые характеристики искомого решения ,по которым восстанавливаются само решение и соответствующая форма границы тела.Следует отметить точное решение В.В.Соколовского для стержня овальной формы,близкой к эллипсу [87] ,и решение М.П.Галина [21] для стержней с сечением,близким к полигональному ( в частности ,близким к прямоугольному сечению). Л.М.Качанов [51] вариационным методом получил решение для стержня квадратного сечения.В работе [4] дано приближенное решение для прямоугольного сечения методом прямых ,когда пластические зоны развиваются лишь вблизи одной пары сторон.Авторы монографии [5] посвятили свою работу неоднородным упруго-пластическим задачам и дали краткий обзор по теории кручения упруго-пластических стержней. В работе [28] рассмотрена задача упруго-пластического кручения призматических стержней с кусочно- постоянным поперечным рапределением упругих и упруго-пластических свойств.В статье [35] выводится аналитическая зависимость для определения упруго-пластического изгиба свободно опертой балки прямоугольного поперечного сечения и нагруженной силой в середине пролета.Рассматривается случай параболической аппроксимации участка упрочнения. В работе [103] изложен практический метод расчета пространственных форм по предельному состоянию.Метод позволяет производить расчет усилий и прогибов,обеспечивая при этом подбор сечений стержней.Обсуждается вопрос о повышении скорости сходимости получающегося,в том числе конструкция с большим числом элементов. Д.Жудин [36] дает теоретический и экспериментальный анализ упруго- пластического состояния несущей способности однопролетных и неразрезанных балок при подвижной и повторной нагрузках.В.М.Деренковским [29] разработана методика определения несущей способнсти стержней из гнутых профилей при расчетах на растяжение (сжатие),изгиб и сжатие с учетом неоднородных по сечению упруго-пластических свойств материала. Расчетам элементов конструкций с помощью ЭВМ и разработкам численных методов решения задач теории упругости и пластичности посвящены работы [50,54,77,89,94].Больших успехов достигли советские ученые в области вычислительной математики и ее приложениях [9,25,63,83,90]. Интерес ,проявляемый за последние десятилетия к вопросам пластичности при переменных нагружениях и наличии конечных областей пластических деформаций ,не случаен.Необратные процессы,возникающие при переменных (повторных и знакопеременных) упурго-пластических нагружениях,приводят к возникновению новых качествнных эффектов ,не наблюдаемых при нагружении из исходного состояния.Сюда относятся:вторичная пластическая деформация,циклическое упрочнение,разупрочнение и циклическая анизотропия,значительное накполение повреждений ,физическая и конструктивная приспособляемость и т.д.Этим объясняется возрастающий интерес к изучению вопросов циклического упруго-пластического деформирования. Из обзора ,приведенного в работах [67] и др.,следует,что первые исследования ,связанные с циклической упруго-пластической деформацией материала выполнены И.Баушингером,Р.Мазингом,Х.Шойи,Р.Вулли.Ими предложены различные гипотезы ,позволяющие построить зависимости между напряжениями и деформациями при переменных нагружениях ,если известна только диаграмма “исходно” нагружения .Развитию и обобщению этих работ посвящены исследования В.В.Москвитина [67,68],А.П.Гусенкова и Р.М.Шнейдеровича [27,97] С.В.Серенсена [85],Ю.Н.Шевченко [94,95],В.В.Колокольчикова [55-57] и др. В монографиях В.В.Москвитина [67,68] исследовано напряженно-деформированное состояние упруго-пластических и вязко-пластических тел при переменных нагружениях, сформулированы теоремы о вторичных пластических деформациях и переменных нагружениях.С помощью доказанной теоремы о переменном нагружении выведены конечные формулы ,определяющие напряжения и деформации при произвольном количестве нагружений.Рассмотрены некоторые вопросы циклической прочности,устойчивости с учетом предыстории. Большой экспериментальный материал по переменным нагружениям получен в рвботах [27,97]. В статье А.П.Гусенкова и Г.В.Москвитина [26] проводится ана лиз диаграмм циклического упруго-пластического деформирования на примере материалов о контрастными циклическими свойствами и показаны возможные уточнения, упрощения, интерпретации диаграмм о целью приложения в решении задач циклической пластичности. Указаны основные особенности сопротивления материалов циклическому упруго-пластическому деформированию и определен масштабный коэффициент обобщенного принципа Мазинга-Москвитина. В работах [55—57] В.В.Колокольчиковым исследован процесс деформирования среды в условиях нелинейной вязко-упругости и не- классической пластичности, сформулированы постановки задач о моментных напряжениях при циклических упруго-пластических нагружениях и даны обобщения теоремы о переменных нагружениях с учетом пьезоэлектрического эффекта. Вопросы устойчивости упруго-пластических стержней, пластин и оболочек с учетом начальных напряжений, вызванных предшествующим пластическим деформированием, и вида напряженного состояния исследованы В.Д.Гаджиевым [23-24]. Вопрооам термопластичности при переменных нагружениях поовя- щены работы Ю.Н.Шевченко и его учеников [94-95]. В монографии [95] приведены основные уравнения и дана постановка пространственных задач термопластичности с учетом деформации ползучести и истории нагружения. Изучению упруго-пластических свойств материалов при циклических и сложных нагружениях посвящены работы [22,37,52,58,61,73,76, 92].Вопросы расчета стержней,пластинок и оболочек при циклических нагружениях рассмотрены также в работах [ 15,20,45,70,82,93,102]. Отметим, что расчет упруго-пластической задачи при циклическом нагружении теоно связан с большими трудностями как масштабного, так и вычислительного характера. Реализация таких расчетов без применения ЭВМ не представляется возможной. Поэтому в настоящее время актуальными становился алгоритмические методы решения задачи теории упругости и пластичности, разработанные В.К.Кабуло- вым и его учениками [15,46-48,59,89]. Т.Буриевым [12-15] сформулирован ряд краевых задач по статическому и динамическому расчету несущих элементов тонкостенных конструкций типа плит, балок, оболочек и разработаны экономичные эффективные алгоритмы их решения при повторных и переменных упруго-пластических нагружениях. Предлагаются некоторые споообы регулировки скорости сходимости этих алгоритмов, В работах [1,16] предложены некоторые подходы к анализу деформирования упруго-пластических тел с учетом накопленных повреждений, решены краевые задачи об упруго-пластическом изгибе балок, осесимметричных круглых пластин и цилиндрических оболочек о учетом вторичных плаотических деформаций при разгрузке и при последующих переменных нагружениях. В статье [80] рассмотрены упруго-пластические колебания балок при повторно-переменном нагружении. Построена вычислительная схема решения краевых задач динамичеокого расчета балок методами Бубнова-Галеркина, Рунге-Кутта и на ее основе предложена автоматизированная система расчета балок. В работе [71] изучаютоя упруго-пластические колебания стержней произвольного сечения при кручениях о учетом разгрузки. На основе теории малых упруго-пластических деформаций в работе [86] решается задача о брусе при совместном действии изгиба, кручения и растяжения. Из приведенного обзора следует, что количество работ по расчету пространственных стержней при упругих и упруго-пластических нагружениях сравнительно мало. Причем, при построении теории используются различные упрощения и ЭВМ применяются лишь для реализации отдельных аспектов расчета, В связи с этим остаютоя открытыми такие актуальные вопрооы, как полный отатический расчет упруго-пластичеокого отержия и исследование напряженно-деформированного ооотояния при оовмеотном действии продольных, поперечных, крутильных, упруго-плаотичеоких нагружений и разгружений (проотранственно-перомеиных нагружений и разгружений). Исходя из анализа перечисленных выше работ, отметим следующее: Появление новых материалов, необходимость повышения эксплуатационных скоростей и температур, снижения веса, уменьшения объема, увеличения сроков эксплуатации - вое это вызывает потребность совершенствования методов расчета. Возникает необходимость лучшего понимания особенности на- пряженного-деформированного состояния стержня в неблагоприятных условиях и влияния полей остаточных напряжений, возникающих при технологическом процессе и циклическом нагружении. Диссертационная работа посвящена построению математической модели стержней на основе гипотезы, предложенной В.3.Власовым [18,19] и Г.Ю.Джанелидзе [30], и обобщенной В.К.Кабуловьш [47] для случая перемещения точек отержня при совместном действии продольных, поперечных и крутильных о ил. Выводятся уравнения равновесия отержня при проотранотвенно-переменном упруго-пласти- чеоком нагружении и раэгружении, вывод которых осуществляется на основе теории малых упруго-пластических деформаций, разработанной А.А.Ильюшиным, В.В.Москвитиным [40,67]. В диссертации на основе метода конечных разностей с комбинацией итерационного процесса производится построение вычислительных схем для исследования напряженно-деформированного состояния стержня при пространственно-переменном упруго-пластическом нагружении и разгружении. Работа оостоит из введения, трех глав, заключения, списка попользованной литературы и приложения. В первой главе описывается разработка алгоритмов решения cтатических задач стержней при пространотвонно-переменных упруго-пластичеcких нагружениях. В первом разделе приводится постановка краевой задачи cтержней и о помощью вариационного принципа Лагранжа выводятоя оио- темы нелинейных дифференциальных уравнений равновесия с естественными граничными условиями при проотранственно-переменных нагружениях стержней. Как известно, если при переменных упругопластических нагружениях величина текущей внешней нагрузки превышает величину нагрузки предыдущего полуцикла, то нарушаются условия теоремы о переменном нагружении. Поэтому при формулировке краевых задач, согласно работам [12,15], текущие компоненты напряжений выражаютоя через текущие компоненты деформации. При этом используется принцип Мазинга-Москвитина и обобщенная диаграмма циклического деформирования Гусенкова-Шнейдеровича. Во втором разделе предлагаются разработанные вычислительные алгоритмы решения краевых задач стержня при пространственно-пере- менных упруго-пластических нагружениях и разгружениях на основе метода конечных разноотей. К решению разиоотных краевых задач применяется метод матричной прогонки с комбинацией модифицированного метода упругих решений (неявный итерационный процеос). В третьем разделе рассматривается вопрос реализации на ЭВМ разработанного алгоритма расчета стержней при пространственно- перешенных нагружениях и разгружениях с учетом вторичных пластических деформаций. Приведена блок-схема программы автоматизированной системы для реализации статического расчета упруго-плас- тических стержней и дано описание программы, которая составлена на языке АЛГ0Л-60 и реализована на БЭСМ-6. Во второй главе приведен упруго-пластический расчет стержня при изгибе в одной плоскости и пространственном нагружении из "естественного" состояния. Дан числоиных анализ сходимости метода конечных разностей и иооледуетоя напряженно-деформированное состояние упругих стержней при оовмеотном действии продольных, поперечных и крутильных оил. Далее анализируетоп чиоленная оходимость метода конечных разноотей и метода последовательных приближений при раочете упруго-плаотичеоких отержней. При различных интеноивноотях нагрузки анализируетоя решение задачи в зависимости от количества итераций, весовых узлов Гауооа и шага сетки. Иооледуютоя напряженно-деформированное ооотояние упругопластического изгиба балок без учета гипотезы плооких оечений о различными краевыми уоловиями и упруго-плаотичеокое деформирование конеоля при торцевом нагружении. В третьей главе рассматриваются проотранотвенно-перемеиные нагружения упруго-плаотических отержней. Анализируетоя характер сходимости приведенного вычислительного алгоритма в зависимости от степени развития плаотических деформаций, краевых условий,количества узлов сетки, числа нагружений и от программы нагружения. Иооледовано напряженно-деформированное соотояние отержней о учетом упругой разгрузки и вторичных пластичеоких деформаций. Приведен сравнительный анализ остаточных расчетных величин о помощью теоремы об упругой разгрузки и вторичных плаотических деформациях Илыошина-Мооквитина. Также проведен упруго-пластичеотический расчет стержней при различных программах пространственного нагружения о учетом обобщенного принципа Мазинга-Мооквитина, позволяющего учитывать циклическое упрочнение, разупрочнение и деформационную анизотропию. Результаты раочетов представлены в виде таблиц и графиков. |
