ўқитувчи. Продолжение табл (1). Исследование УпругоПластических Состояний Стержней при ПространственноПеременных Нагружениях
 Скачать 182.35 Kb. Скачать 182.35 Kb.
|
|
ГЛАВА 1 РАЗРАБОТКА АЛГОРИТМОВ РЕШЕНИЯ СТАТИЧЕСКИХ ЗАДАЧ СТЕРЖНЕЙ ПРИ ПРОСТРАНСТВЕННО-ПЕРЕМЕННЫХ УПРУГО-ПЛАСТИЧЕСКИХ НАГРУЖЕНИЯХ Настоящая глава ооотоит из трех разделов. В первом разделе даетоя постановка задачи при совместном действии продольных, поперечных и крутильных сил. Устанавливается зависимость между напряжениями и деформациями при повторно-переменном упруго-пластическом нагружении и выводится математическая модель на основе вариационного принципа Лагранжа. Во втором разделе на основе метода конечных разностей строится вычислительный алгоритм. В третьем разделе приводится реализационная схема для БЭСМ-6 по разработанному вычислительному алгоритму. I.I. Постановка краевой задачи Рассмотрим призматический стержень произвольного сечения при воздействии внешних сил [18,19,32,47-48,88]. Для этого ось OX направим по длине cтержня, а оcи OZ и OY - по поперечному cечению (рио.2.2.1). Перемещение центральной линии cтержня обозначим через U, V, W; углы наклона каоательной к упругой линии при чистом изгибе -£1, £2 ; углы поперечного сдвига β1, β2; а угол закручивания - через θ , погонный угол закрутки-ν. Тогда на основании статичеcких гипотез устанавливается однозначная зависимость между перемещениями стержня U1(x,y,z), U2(x,y,z), U3(x,y,z), и U(x), V(x), W(x) и т.д. Перемещения точек cтержня при совместном действии продольных, поперечных и крутильных cил можно представить в виде [18,46]  U1=U - Ƶԃ1-Yԃ2+ϕʋ+α1β1 +α2β2 ; U1=U - Ƶԃ1-Yԃ2+ϕʋ+α1β1 +α2β2 ; U2 = V + Ƶθ ; (I.I.I) U3 =W – yθ , Теперь, согласно формулы Коши, с учетом формул (I.I.I) вычисляем компоненты деформации:  L11 = 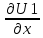 = = 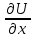 - ƶ - ƶ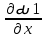 - y - y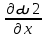 +ϕ(ƶ,y) +ϕ(ƶ,y)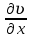 +α1 +α1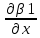 + α2 + α2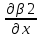 ; ;L12 = 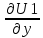 + + 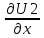 = = 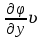 + + 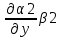 + + 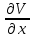 + + 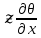 - ԃ2 ; (I.I.2) - ԃ2 ; (I.I.2)L13 = 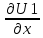 + + 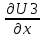 = = 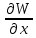 - y - y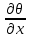 + + 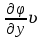 + + 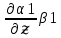 - ԃ1 ; - ԃ1 ;L22 = L33 = L23 =0 Зависимость между компонентами тензора напряжения и деформации определяется из теории малых упруго – пластических деформаций А.А. Ильюшина – В. В. Москвитина [ 39-40, 66- 67] (рис.I.I.I). Известно , что, если при повторных и переменных упруго-пластических нагружениях величина текущей внешней нагрузки превышает величину нагрузки предыдущего полуцикла, то нарушаются условия теоремы о переменном нагружении. Поэтому для решения краевых задач, согласно работам ( 12,16), текущие компоненты напряжений выражены через текущие компоненты напряжений выражены через текущие компоненты деформации. Выполняя необходимые операции в области первого, второго и произвольного количества упруго – пластических нагружений или разгруженний с номером К , получаем соотношения между напряжениями ( 12,67):  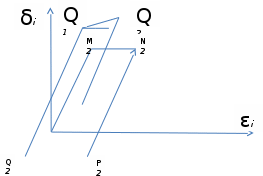 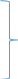 δ11(k) = 3G(( 1-w(k)) l11(k) – w(k)l110(k-1) + ∑W 0(k-m) ( l110(k-m) – l11 0(k-m-1))) , δ12(k) = G(( 1-w(k)) l12(k) – w(k)l120(k-1) + ∑W 0(k-m) ( l120(k-m) – l12 0(k-m-1))) , δ13(k) = 3G(( 1-w(k)) l13(k) – w(k)l130(k-1) + ∑W 0(k-m) ( l130(k-m) – l13 0(k-m-1))) , δ22(k) = δ33(k) = δ23(k) = 0 , ( I.I.3) где l110(0) =l12 0(0) = l130(0) =0 B случае линейного упрочнения материала функция пластичности ѡ (к) вычисляется по формулам : при К=I  0 , при l1 <1 , ѡ(1) = ( I.I.4) ƛ ( 1- 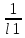 ) , при l ≥1 . ) , при l ≥1 .и при К ≥2 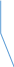 0 , при l1(к) <ԃк , ѡ(к) = ( I.I..5) ƛ ( 1- 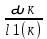 ) , при l1(к) ≥ ԃк . ) , при l1(к) ≥ ԃк .здесь l1(к) = li(k) ̸ ls , k = 1,2,…., l10(1) , ѡ0(1) соответствуют значениям l1(1) , ѡ(1) в точке N , αl10(2) , ѡ0(2) - значения l1(2) , ѡ(2) в точке Q ( см. рис.I.I.I), li(k) = ⅔√( l11(k))2+ ¾ [( l12(k))2 +( l13(k))2] . (I.I.6) на основе обобщенного принципа Мазинга [ 26,27] с помощью параметра ᾱк учитываются циклические свойства материалов ,т.е. рассматриваются циклические идеальные , упрочняющиеся и разупрочняющиеся материалы. Параметры ᾱк могут быть представлены в виде [26] ᾱк = ᾱ1 ( к-1)x ( I.I.7) здесь ᾱ1 , z - константы материала. При этом для циклически упрочняющихся материалов ᾱк ˃2 , для разупрочняющихся ᾱк ˃2, А дляциклически идеалных материалов ᾱк ˃2. Вводя различные значения масштабного коэффициента четных и нечетных полуциклов нагружения для ᾱк , можно описать также упруго – пластические свойства циклически анизотропных материалов : ᾱк = ᾱ2 ( к-1)x + 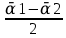 [ 1- (-1)к]( к-1)x . (I.I.8) [ 1- (-1)к]( к-1)x . (I.I.8)Константы материалов ᾱ1 , ᾱ2 , z определяются экспериментальню. Для вывода дифференциальных уравнений равновесия стержней при пространственном нагружении используется вариационный принцип Лагранжа [ 47, 18] δ (- П+А) =0 ; (I.I.9) где δП= ∫∑ δ1i(k) δ l1i(k) dV (I.I.10)  - вариация потенциаьной энергии, а - вариация потенциаьной энергии, аδА= ∫∑Pi(k) δUi(k) dV + ∫∑qi(k) δUi(k) dS1 x +∫∑fi(k) δUi(k) dS2 (I.I.11) Вариация работы внешних сил. Здесь через P i(k) обозначены составляющие компоненты объмных сил, отнесенные к единице объема, через qi(k) – торцевые составляющие силы, отнесенные к единице площади поперечных сечений, действующие на торцах х=0 и х=l , и через fi(k) поверхностные составляющие силы, отнесенные к единице площади поверхности стержня. На основе вариационного принципа Лагранжа (I.I.9) с использованием с оотношения Коши (I.I.2) и связи между напряжениями и деформациями при условии несжимаемости материала (I.I.3) выводится система нелинейных дифференциальныхуравнений с естественными граничными условиями в векторной форме 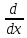 [ ( AУП- АПЛ(К)) [ ( AУП- АПЛ(К)) 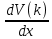 + ( BУП – BПЛ(К))V(k)] + ( CУП – СПЛ(к)) + ( BУП – BПЛ(К))V(k)] + ( CУП – СПЛ(к)) 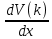 + (DУП – DПЛ(К)) V(k) =F(K) + + (DУП – DПЛ(К)) V(k) =F(K) + 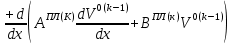 + + 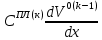 + + 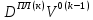 + + 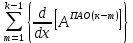 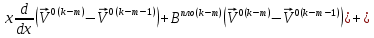 (I.I.12) 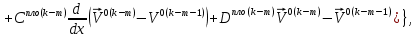 {-( 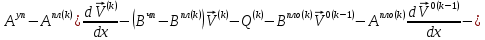 (I.I.13) 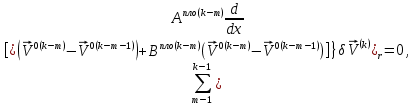 Где 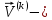 вектор-функции 9-го порядка; вектор-функции 9-го порядка; 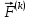 , ,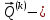 векторы 9-го порядка; векторы 9-го порядка; 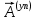 , , 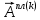 , , 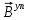 , , 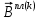 , ,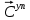 , , 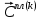 , , 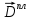 , , 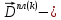 квадратные матрицы 9-го порядка квадратные матрицы 9-го порядкаЭлементы этих матриц и векторов имеют соответственно следующий вид: 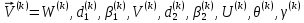 }; };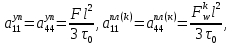 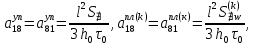 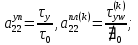 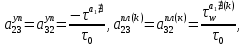 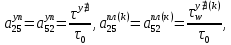 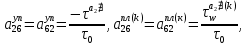 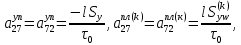 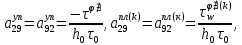 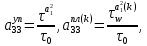 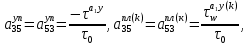 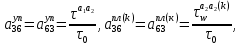 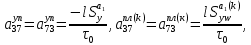 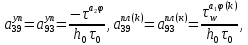 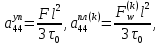 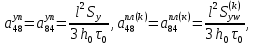 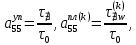 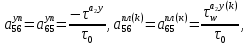 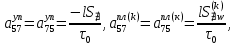 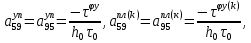 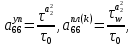 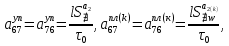 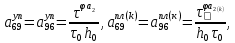 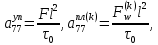 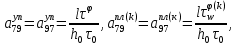 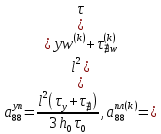 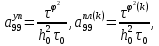 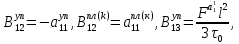 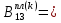 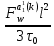 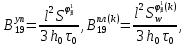 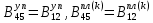 , ,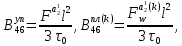 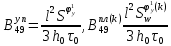 , ,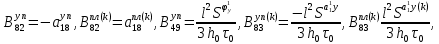 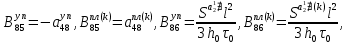 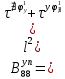 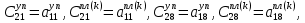 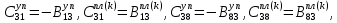 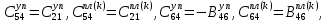 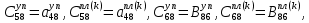 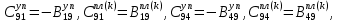 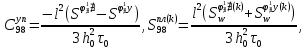 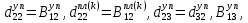 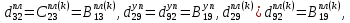 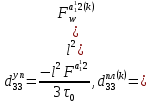 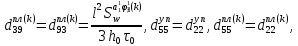 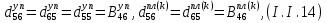 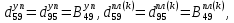 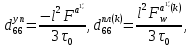 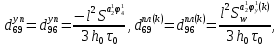 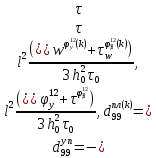 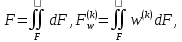 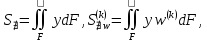 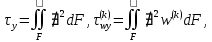 |
