ОМПС. Распутин РГР 1 (Трофимович основа). Исследование устойчивости движения тележки
 Скачать 340.25 Kb. Скачать 340.25 Kb.
|
|
Министерство транспорта Российской Федерации Федеральное агентство железнодорожного транспорта Федеральное государственное бюджетное образовательное учреждение высшего образования «Дальневосточный государственный университет путей сообщения» Кафедра «Транспорт железных дорог» ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ДВИЖЕНИЯ ТЕЛЕЖКИ Расчётно-графическая работа дисциплина «Основы механики подвижного состава» РГР 23.05.03. 01.00. СО132ЛОК Студент _____ Распутин Д. С (подпись, дата) Доцент _____ Трофимович В.В. (подпись, дата) Хабаровск 2022 СодержаниеВведение 4 1КИНЕМАТИЧЕСКАЯ СХЕМА ПРИ БОКОВЫХ КОЛЕБАНИЯХ 5 2РАСЧЕТ ИНЕРЦИОННЫХ ХАРАКТЕРИСТИК ТЕЛЕЖКИ 6 3СОСТАВЛЕНИЕ УРАВНЕНИЙ БОКОВЫХ КОЛЕБАНИЙ РАСЧЕТНОЙ МОДЕЛИ 8 4ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ МАТРИЦЫ УРАВНЕНИЙ 12 5ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ СКОРОСТИ ДВИЖЕНИЯ ТЕЛЕЖКИ 15 Заключение 19 Библиографический список 20 ВведениеПри оценке качества подвижного состава (ПС) существенное значение имеют динамические показатели, определяющие безопасность движения, уровень нагрузки несущих элементов конструкций, интенсивность износа отдельных элементов и показатели комфорта. В решении задачи достижения высоких ходовых качеств рельсовых экипажей особое значение имеет обеспечение устойчивости их невозмущенного движения в диапазоне рабочих скоростей. В данной расчетно-графической работе необходимо определить критическую скорость движения тележки, при которой она теряет устойчивость и анализ влияния анализируемого параметра тележки на величину критической скорости. Для достижения этой цели решаются следующие задачи: разрабатывается кинематическая схема при боковых колебаниях, составляются уравнения боковых колебаний расчетной модели, рассчитываются коэффициенты крипа, определяется критическая скорость движения тележки. В заключении данного проекта, опираясь на полученные данные расчетов, необходимо сделать вывод о правильности выбора параметров рессорного подвешивания. КИНЕМАТИЧЕСКАЯ СХЕМА ПРИ БОКОВЫХ КОЛЕБАНИЯХРасчетная кинематическая схема тележки (рис. 1.1) упрощена рядом допущений: Рассматривается движение по прямому ровному горизонтальному пути; Путь считается абсолютно жестким в горизонтальном направлении; Жесткость связи КП с рамой тележки в продольном направлении велика, поэтому продольные перемещения букс относительно рамы тележки не учитываются; Демпфирующие свойства буксовых поводков считаются малыми. Кинематическая схема тележки (рис. 1.1) позволяет учесть колебания бокового относа 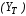 и влияние и влияние 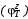 тележки, колебания бокового относа КП тележки, колебания бокового относа КП 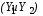 . .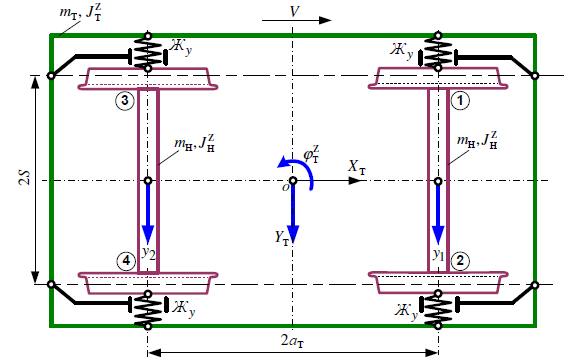 Рисунок 1 - Расчетная кинематическая схема тележки На расчетной кинематической схеме приняты следующие обозначения: 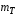 - масса подрессоренной части тележки, т; - масса подрессоренной части тележки, т; 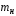 – масса неподрессоренной части в расчете на одну колесную пару, т; – масса неподрессоренной части в расчете на одну колесную пару, т;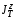 – момент инерции подрессоренной части тележки относительно оси – момент инерции подрессоренной части тележки относительно оси 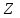 , тм2; , тм2;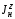 – момент инерции неподрессоренной части тележки относительно оси – момент инерции неподрессоренной части тележки относительно оси 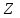 , тм2; , тм2;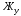 – жесткость поводков в поперечном направлении (жесткость связи КП с рамой тележки), кН/м; – жесткость поводков в поперечном направлении (жесткость связи КП с рамой тележки), кН/м;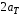 – жесткая база тележки, м; – жесткая база тележки, м;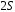 – расстояние между опорными точками колес на рельсы (рекомендуется принять – расстояние между опорными точками колес на рельсы (рекомендуется принять 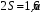 ). ).РАСЧЕТ ИНЕРЦИОННЫХ ХАРАКТЕРИСТИК ТЕЛЕЖКИМомент инерции тележки и неподрессоренной массы относительно оси Z определяются пересчетом от экипажа прототипа. Инерционные, массовые и геометрические характеристики экипажа – прототипа принимаются в зависимости от подрессоренной массы тележки 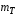 . .По исходным данным 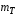 =20 т, то есть =20 т, то есть 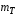 < 22 т, а значит параметры прототипа принимаются: < 22 т, а значит параметры прототипа принимаются:Масса тележки прототипа - 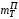 =13,8 т; Момент инерции относительно оси Z - =13,8 т; Момент инерции относительно оси Z - 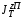 =27 тм2; Половина базы =27 тм2; Половина базы 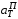 =1,5м. =1,5м.Момент инерции неподрессоренной части прототипа в обоих случаях принимается 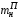 =5,25 т и =5,25 т и 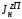 =2,4 тм2. =2,4 тм2.Момент инерции тележки относительно оси Z при поправке на массу определяется: 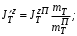 (2.1) (2.1)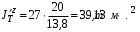 (2.2) (2.2)При введении поправки на геометрические размеры окончательно момент инерции тележки определяется: 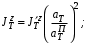 (2.3) (2.3)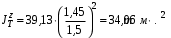 (2.4) (2.4)Момент инерции неподрессоренной части относительно оси Z определяется: 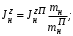 (2.5) (2.5)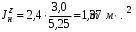 (2.6) (2.6)СОСТАВЛЕНИЕ УРАВНЕНИЙ БОКОВЫХ КОЛЕБАНИЙ РАСЧЕТНОЙ МОДЕЛИУравнения составляются для каждой массы отдельно. Схема замещения для рамы тележки будет иметь вид (рис. 3.1). 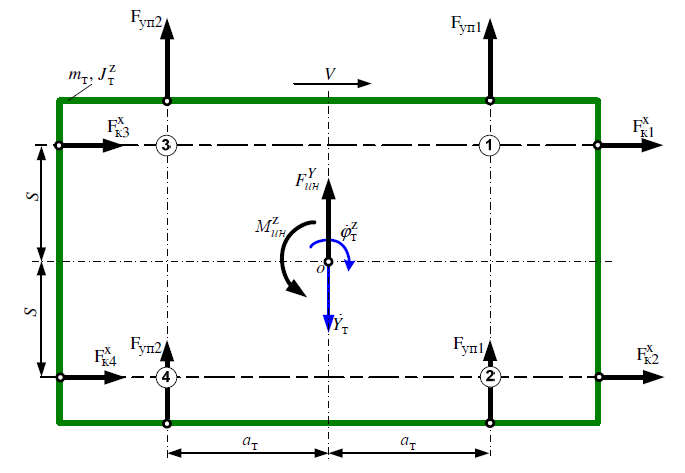 Рис. 3.1. Расчетная схема замещения рамы тележки при боковых колебаниях Уравнение колебания бокового относа тележки имеет вид: 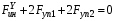 (3.1) (3.1)Входящие в это уравнение силы определяются: − сила инерции подрессоренной части тележки по оси Y:  (3.2) (3.2)где  - поперечное ускорение тележки; - поперечное ускорение тележки;− сила упругости в поперечном направлении: 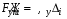 (3.3) (3.3)где 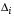 - поперечное перемещение букс относительно рамы тележки (i=1,2). - поперечное перемещение букс относительно рамы тележки (i=1,2).При боковом относе и повороте тележки вокруг вертикальной оси, а также с учетом бокового относа колесных пар ∆1 и ∆2 определяются: 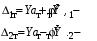 (3.4) (3.4)Подставим формулы (3.2) и (3.3) с учетом (3.4) в уравнение (3.1), приведем подобные слагаемые и получим уравнение колебания бокового относа тележки, которое имеет следующий вид: 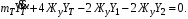 (3.5) (3.5)Составим уравнение колебания виляния тележки, для этого необходимо найти сумму моментов сил относительно оси (положительное направление принять по часовой стрелке), которая имеет вид: 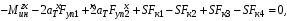 (3.6) (3.6)где 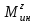 - главный момент сил инерции относительно оси Z, определяется по формуле (3.7); - главный момент сил инерции относительно оси Z, определяется по формуле (3.7); 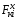 - силы, действующие в плоскости контакта колеса и рельса в продольном направлении, определяются по формуле (3.8). - силы, действующие в плоскости контакта колеса и рельса в продольном направлении, определяются по формуле (3.8).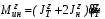 (3.7) (3.7)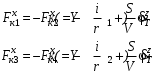 (3.8) (3.8)где i – конусность поверхности колеса (i = 0,1); r – радиус колеса по кругу катания (r = 0,625 м); к – коэффициент крипа (к = 14000 кН). Подставляя силы по формулам (3.3), (3.4), (3.7) и (3.8) в уравнение (3.6), затем приведя подобные слагаемые, получим окончательное уравнение колебания виляния тележки, которое имеет вид: 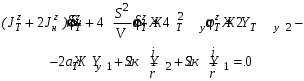 (3.9) (3.9)Для составления уравнений колебаний бокового относа колесных пар используется схема замещения, которая для первой колесной пары имеет вид, показанный на рис. 3.2. 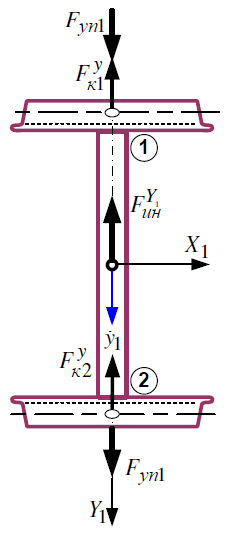 Рис. 3.2. Расчетная схема замещения первой колесной пары Сумма проекций всех сил на ось  имеет вид: имеет вид: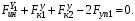 (3.10) (3.10)Входящие в это уравнение силы находятся: − 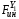 - сила инерции неподрессоренной части по оси : - сила инерции неподрессоренной части по оси :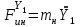 (3.11) (3.11)− 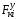 - силы, действующие в плоскости контакта колеса и рельса в поперечном направлении: - силы, действующие в плоскости контакта колеса и рельса в поперечном направлении: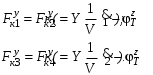 (3.12) (3.12)Подставим формулы (3.11), (3.12), (3.4) и (3.3) в уравнение (3.10), приведем подобные слагаемые и получим уравнение колебания бокового относа первой колесной пары, которое имеет следующий вид: 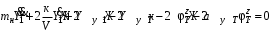 (3.13) (3.13)Аналогичным образом получаем уравнение колебания бокового относа второй колесной пары. Уравнение имеет следующий вид: 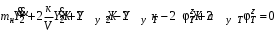 (3.14) (3.14)Все полученные уравнения сводим в одну систему уравнений, которая имеет следующий вид: 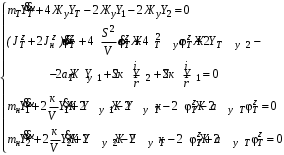 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ МАТРИЦЫ УРАВНЕНИЙСведем уравнения системы, полученной в пункте 3, к нормальной форме. Для этого необходимо разделить каждое из уравнений на коэффициент при второй производной и перенести все члены, кроме вторых производных, в правые части уравнений. Полученные уравнения представлены ниже: 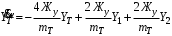 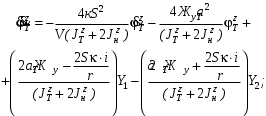 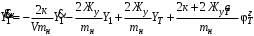 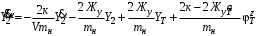 Введем следующие обозначения: 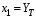 , , 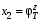 , , 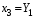 , , 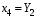 , , 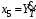 , , 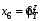 , , 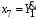 , , 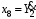 . Подставим эти обозначения в выше приведенные уравнения. . Подставим эти обозначения в выше приведенные уравнения.Уравнение колебания бокового относа тележки в нормальной форме будет иметь вид: 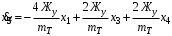 Коэффициенты перед неизвестными будут иметь вид: 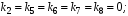 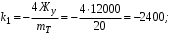 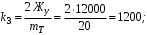 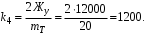 Уравнение колебания виляния тележки в нормальной форме будет иметь вид: 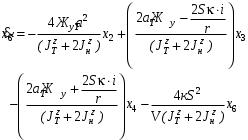 Коэффициенты перед неизвестными будут иметь вид: 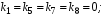 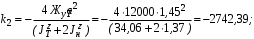 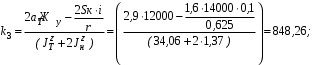 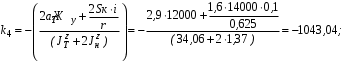 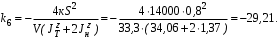 Уравнение колебания бокового относа первой колесной пары в нормальной форме будет иметь вид: 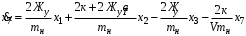 Коэффициенты перед неизвестными будут иметь вид: 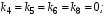 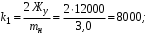 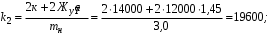 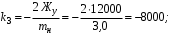 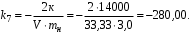 Уравнение колебания бокового относа второй колесной пары в нормальной форме будет иметь вид: 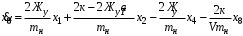 Коэффициенты перед неизвестными будут иметь вид: 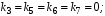 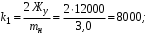 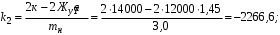 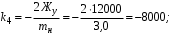 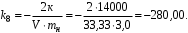 Запишем уравнения с коэффициентами в численном виде: 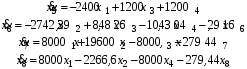 Для упрощения расчетов матрицу коэффициентов уравнений необходимо представить в виде таблицы 4.1. Таблица 4.1 – Матрица коэффициентов уравнений
ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ СКОРОСТИ ДВИЖЕНИЯ ТЕЛЕЖКИДля определения критической скорости движения тележки необходимо получить ряд решений для постепенно увеличивающих значений скорости движения тележки. Результаты расчета рекомендуется представить в таблице 5.1. Таблица 5.1. – Расчет максимально вещественной части
Рассчитаем собственные числа матрицы А (табл. 4.1) и максимальную вещественную часть корней, используя программу Maple приведенную ниже (расчет приведен для скорости V=120/3,6 км/ч). 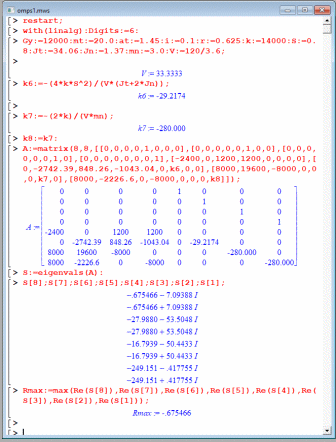 Анализируемым параметром является 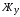 . . Рассчитаем два значения анализируемого параметра: 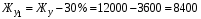 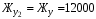 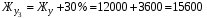 По данным таблицы 5.1 строим график  , представленный ниже. , представленный ниже.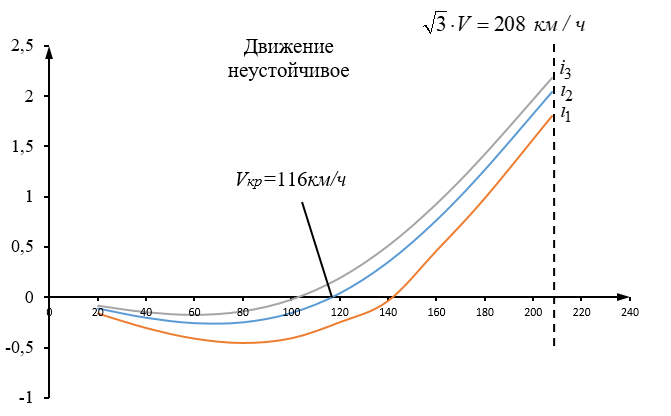 Рис. 5.1 – Зависимость максимально вещественной части от скорости движения Вывод: По графику зависимости максимальной вещественной части от скорости движения видно, что критическая скорость данной тележки равна 116 км/ч, что не превышает максимальную скорость 208 км/ч. Из-за чего движение тележки нельзя считать устойчивым и параметры рессорного подвешивания выбраны неверно. Также по графику видно, что чем больше анализируемый параметр Жу (поперечная жесткость связи КП с рамой тележки), тем меньше критическая скорость. А если уменьшать анализируемы параметр, то критическая скорость становится больше. ЗаключениеВ ходе выполнения расчетно-графической работы осуществили следующее: определили критическую скорость движения тележки, при которой она теряет устойчивость, и проанализировали влияние анализируемого параметра тележки на величину критической скорости. Для достижения этой цели решили следующие задачи: разработали кинематическую схему при боковых колебаниях, составили уравнения боковых колебаний расчетной модели, рассчитали жёсткость РП и определили критическую скорость движения тележки. Анализируя всю расчетно-графическую работу, удалось выяснить, что для данной тележки была неправильно подобрана жёсткость РП части тележки, из-за чего движения тележки неустойчиво и имеет критическую скорость. Также поперечная жёсткость РП (анализируемый параметр) устроена так, что чем меньше параметр, тем больше критическая скорость, и наоборот. Библиографический списокТрофимович, В. В. Исследование устойчивости движения тележки: метод. рекомендации для выполнения расчетно-графической работы №1 / В.В. Трофимович. – Хабаровск: 2019. – 19 с.: ил. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 .
.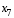 и
и 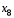 .
.
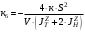
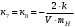
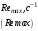 -30%
-30%