статистика. 185943 статистика социальная. Исследование, выяснив сведения о росте 10 случайным образом выбранных мужчин. Составить таблицу распределения, найти моду, медиану, среднее значение роста (в см)
 Скачать 217 Kb. Скачать 217 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА № 1 Провести статистическое исследование, выяснив сведения о росте 10 случайным образом выбранных мужчин. Составить таблицу распределения, найти моду, медиану, среднее значение роста (в см). Порядок выполнения работы 1. Следует обозначить статистическую совокупность, которая состоит из материально существующих объектов. 2. Сформировать выборку собранных данных по обозначенным признакам, данные упорядочить по возрастанию. 3. Для обработки собранных первичных данных необходимо упорядочить данные – произвести группировку и обобщение отобранных элементов по заданному признаку, обозначить числовые характеристики выборки – произвести сводку. 4. Составить таблицу распределения частот с последовательным заполнением соответствующих столбцов в таблице. 5. Найти размах по формуле R=X(max) – X(min). 6. Вычислить моду (Mо), которая показывает значение, встречающееся чаще других. Для дискретного ряда модой будет являться вариант с наибольшей частотой. Для определения моды интервального ряда сначала определяют модальный интервал (интервал, имеющий наибольшую частоту). Затем в пределах этого интервала находят то значение признака, которое может являться модой. 7. Вычислить медиану M(e), которая характеризует среднее значение. 8. Рассчитать среднее арифметическое значение для обозначенной группы, которая вычисляется по формуле: X=(X1+X2+.....Xn)/ n =?X1 / n. Результаты работы могут быть представлены графически. Решение: Выборка: 182, 182, 171,193,190,189,183,176,178,168 Упорядочим данные: 168, 171, 176, 178,182,182,183,189,190,193 Составим таблицу распределения частот:
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда. R = Xmax - Xmin 193 - 168 = 25 Максимальное значение повторений при x = 182 (f = 2). Следовательно, мода равна 182 Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим xi, при котором накопленная частота S будет больше ∑f/2 = 6. Это значение xi = 183. Таким образом, медиана равна 183 Средняя арифметическая: это среднее слагаемое, около которого колеблются остальные значения, т.е. характеристика среднего роста студентов. Выводы о характере и закономерностях развития изучаемого явления: -разница в росте юношей , составляет 25 см; -средний рост юношей – 182 см; -в среднем рост 183 см не превышает большинство студентов. ЛАБОРАТОРНАЯ РАБОТА № 2. Выберите отрывок текста на русском языке. Определите в тексте количество глаголов и существительных. Считая рассмотренную выборку репрезентативной, определить примерное количество глаголов и существительных в отрывке этого же произведения объёмом 2000 слов. Порядок выполнения работы: 1. Следует выбрать отрывок текста (произвольно) на русском языке из произведения какого-либо писателя, содержащий 50–100 слов или четверостишие (произвольно) какого-либо поэта. 2. Посчитав количество букв в каждом слове отрывка, составить выборку, вариантами которой являются количество букв в слове. 3. Сформировать выборку собранных данных по обозначенным признакам, упорядочив данные значений. 4. Составить вариационные ряды и заполнить соответствующие ячейки таблицы распределения частот. Для этого необходимо разделить алфавит на 3 участка (определить интервал): № 1 – от «а» до «й», № 2 – от «к» до «ф», № 3 – от «х» до «я». 5. Следует составить таблицу распределения частот участков и указать участок наибольшей частоты. 6. Необходимо определить репрезентативность выборки, по формуле Si/S=Mi/N, где N – объём репрезентативной выборки; S – объём генеральной выборки; Mi – частота (кратность) варианты репрезентативной выборки; Si – частота (кратность) варианты генеральной выборки. Затем следует определить моду Mо которая показывает значение, встречающееся чаще других и медиану Mе, которая характеризует среднее значение (пример расчета см. Лабораторная работа № 1, п. 6, п. 7). 7. Сделать выводы. Для анализа воспользуемся стихотворение Анны Ахматовой Он длится без конца — янтарный, тяжкий день! О, как невыразима грусть, как тщетно ожиданье! И снова голосом серебряным олень В зверинце говорит о северном сиянье. И я поверила, что есть прохладный снег И синяя купель для тех, кто нищ и болен, И санок маленьких такой неверный бег Под звоны древние далеких колоколен. Посчитаем количество букв в отрывке: Он2 длится6 без3 конца5 — янтарный8, тяжкий6 день4! О1, как3 невыразима10 грусть6, как3 тщетно6 ожиданье8! И1 снова5 голосом7 серебряным10 олень5 В1 зверинце8 говорит7 о1 северном8 сиянье6. И1 я1 поверила8, что3 есть4 прохладный10 снег4 И1 синяя5 купель6 для3 тех3, кто3 нищ3 и1 болен5, И1 санок5 маленьких9 такой5 неверный8 бег3. Составим ряд распределения количества букв в словах
И построим выборку:
Сформируем выборку количества существительных и глаголов
Составим таблицу частот букв русского алфавита.
Выделим 3 интервала: № 1 – от «а» до «й», № 2 – от «к» до «ф», № 3 – от «х» до «я».
Проанализировав полученный результат, видим, что таблица частот для данной выборки такова максимальная частота у букв «Н» и «Е». В отрывке из 48 слов мы получили 5 глаголов и 11 существительных. Количество глаголов и существительных в отрывке этого же произведения объёмом 2000 слов можно найти, используя определение репрезентативной выборки, по формуле Si/S=Mi/N, где N-объём репрезентативной выборки, S- объём генеральной выборки, Mi- частота (кратность) варианты репрезентативной выборки, Si- частота (кратность) варианты генеральной выборки. 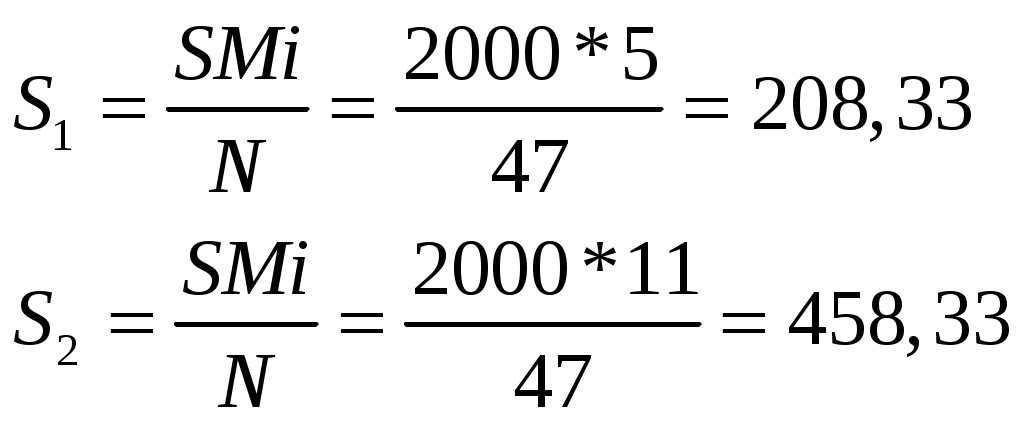 Найдем основные характеристики для данной выборки:
Мода - наиболее часто встречающееся значение признака у единиц данной совокупности. Мода данной выборке нет. Так существует 2 признака с одним значением. Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим xi, при котором накопленная частота S будет больше ∑f/2 = 24. Это значение xi = 5. Таким образом, медиана равна 5. 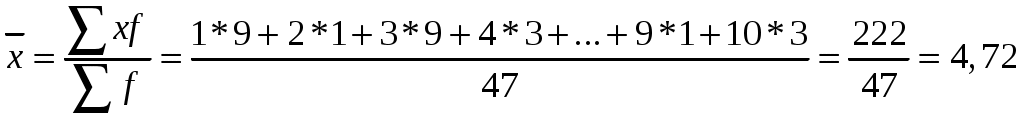 ЛАБОРАТОРНАЯ РАБОТА № 3. На основании опроса 20 случайным образом выбранных старшеклассников школы (9–11кл.) составить таблицу частот (в мин) времени ,затрачиваемого на дорогу от дома до школы. Для наглядности можно построить круговую диаграмму. Порядок выполнения работы: Следует: 1. Произвести статистическое наблюдение методом опроса с целью выяснить необходимую информацию, обозначенную в задании. 2. Сформировать выборку собранных данных по обозначенным признакам, упорядочив данные значений. 3. Составить таблицу частот. 4. Найти размах по формуле: R=Х(max) – Х(min) Рассчитать моду (Mо), которая показывает значение, встречающееся чаще других (пример расчета см. Лабораторная работа № 1, п. 6). Рассчитать медиану (Mе), которая характеризует среднее значение. Пример расчета (см. Лабораторная работа № 1, п. 7). 5. Вычислить среднее арифметическое значение для обозначенной группы, которая вычисляется по формуле: X=(X1+X2+.....Xn)/ n =?X1 / n. 6. Рассчитать интервальный ряд и оптимальное количество интервалов по формуле Стерджесса: n=1+3.322? lgN где n – число групп; N – число единиц совокупности. 7. Рассчитать длину интервала по формуле Xmax - Xmin i=------------------ n 8. Сделать выводы. Результаты работы могут быть представлены графически в виде гистограммы и полигона распределения частот. Эти расчеты можно произвести, используя MS Excel. Решение: Сформируем выборку из 20 школьников:
Упорядочим данные по возрастанию и составим таблицу относительных частот:
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда. R = Xmax - Xmin R = 8 - 1 = 7 Выбираем в качестве начала интервала 5, так как именно на этот интервал приходится наибольшее количество. Медиана соответствует варианту, стоящему в середине ранжированного ряда. Медианным является интервал 5 - 10, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот). Таким образом, 50% единиц совокупности будут меньше по величине 8.75 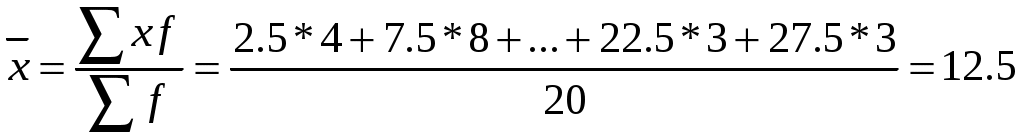 Выявим оптимальное количество интервалов: Но поскольку у нас малое количество исходных данных, то возможно увеличение интервала и уменьшения количества групп. Рассчитаем длину интервала: Составим круговую диаграмму и гистограмму: 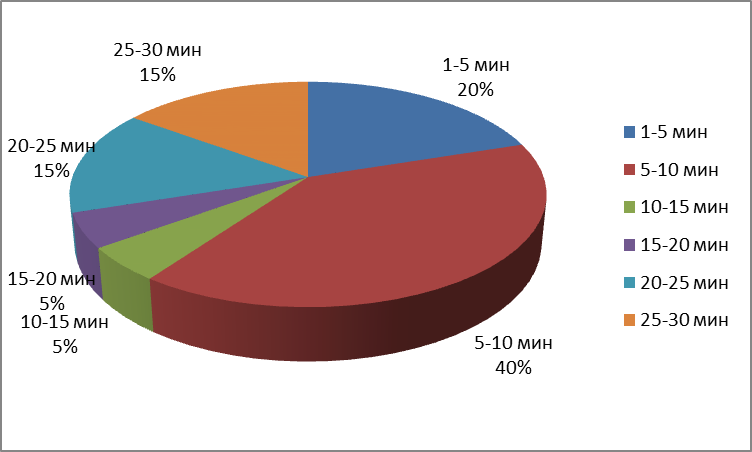 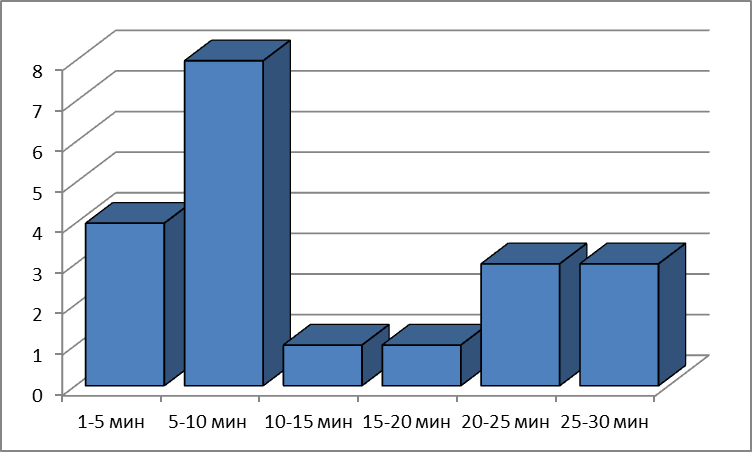 Наглядно данная информация проиллюстрирована с помощью гистограммы и круговой диаграммы. |
