задача 2 статистика. Статистика задача2. Исследование возрастной структуры работников коммерческих предприятий дало следующие результаты 18
 Скачать 40.28 Kb.
|
|
Задача 2. Исследование возрастной структуры работников коммерческих предприятий дало следующие результаты:
Построить интервальный ряд распределения, разбив совокупность на 4 группы с равными интервалами. Изобразить ряд распределения на графике, найти модальную, медианную среднюю величину ряда распределения и сформулировать вывод о возрастной структуре работников. Решение: Размер интервала d находится по формуле:  Xmax, Xmin – соответственно значения максимального и минимального признака; n – количество интервалов. d = (30 - 18) / 4 = 3 года. Для построения интервального ряда необходимо подсчитать число безработных, входящих в каждую группу (Частоты групп). При этом возникает вопрос, в какую группу включать единицы совокупности, у которых значения признака выступают одновременно и верхней, и нижней границами смежных интервалов. Отнесение таких единиц к одной из двух смежных групп рекомендуется осуществлять по принципу полуоткрытого интервала. Т. к. при этом верхние границы интервалов не принадлежат данным интервалам, то соответствующие им единицы совокупности включаются не в данную группу, а в следующую. В последний интервал включаются и Нижняя, и Верхняя границы. Верхняя граница первой группы будет равна (Xmin + d = 18 + 3 = 21 год); второй группы соответственно – 24 лет (21 + 3); третьей – 27 лет (24+3); четвертой – 30 лет (27+3). Таблица 1 - Группы работников по возрасту
Таблица 2 - Разработочная таблица
Продолжение таблицы 2
Итоговые данные по каждой группе из таблицы 2 переносим в конечную таблицу 3, графа 3 и 4. Таблица 3 - Группировка рабочих по возрасту
На рисунке 1 представим гистограмму распределения работников по возрасту. 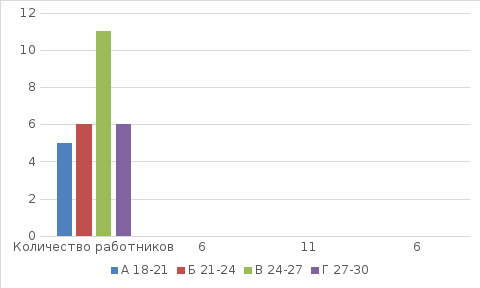 Рис. 1 Гистограмма распределения работников по возрасту Конкретное значение моды для интервального ряда рассчитывается по формуле: 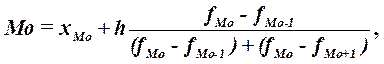 Где ХМo – нижняя граница модального интервала, H –величина модального интервала, fMo – частота модального интервала, fMo-1 – частота интервала, предшествующего модальному, fMo+1 – частота интервала, следующего за модальным. Согласно табл. 3 модальным интервалом построенного ряда является интервал 24-27 лет, так как его частота максимальна. 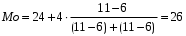 Для рассматриваемой совокупности работников наиболее распространенный возраст характеризуется средней величиной 26 лет. Медианой (  ) называется варианта, которая делит ранжированный ряд на 2 равные части, находится по формуле: где  - нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); - ширина медианного интервала; - накопленная частота интервала, предшествующего медианному; - частота i-го интервала, I = 1,2, …, K; - частота медианного интервала.Для определения медианного интервала необходимо рассчитывать накопленную частоту каждого последующего интервала до тех пор, пока она не превысит ½ суммы накопленных частот (в нашем случае – 28/2 = 14 работников): Таблица 4 - Интервал
Таким образом, медианным является интервал с границами 24-27 лет. Тогда медиана равна: 24 + 3*(1/2*(28-6)/11) = 27 лет. На основе полученных данных можно заключить, что наиболее распространенным, типичным является возраст работников в размере 26 лет. В то же время более половины работников имеет возраст свыше 27 лет при средней его величине 24 года. С ростом численности рабочих до 11 чел. в группе средний возраст повышался, в последней группе численность работников снизилась до 6 чел., а средний возраст повысился до 28 лет. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||