ВКР Каксин (1). Исследование зависимости продольного сжимающего усилия от параметров разработанного компенсирующего устройства расчетноэкспериментальным методом
 Скачать 7.01 Mb. Скачать 7.01 Mb.
|
2 Исследование зависимости продольного сжимающего усилия от параметров разработанного компенсирующего устройства расчетно-экспериментальным методом2.1 Обзор работ, посвященных обеспечению стабилизации положенияподводных переходов газонефтепроводов Как было сказано выше, потеря стабилизации положения подводных участков трубопроводов приводит к аварийным ситуациям и выводу трубопровода из эксплуатации. В большинстве случаев потеря стабилизации положения трубопровода (в том числе и арочные выбросы) происходит за счет воздействия сжимающих продольных усилий, которые необходимо предотвращать или снижать. В работах [12,16] было подробно рассмотрены методы обеспечения пространственной устойчивости газопровода на обводненных участках трассы с учетом влияния переменных грунтовых условий (водонасыщение, предельное сопротивление сдвигу и сцепление). Авторы рассматривали участок газопровода, на котором возникла потеря проектного положения трубопровода в форме арки изза паводка, а также увеличения температуры транспортируемого продукта – газа. Согласно подходу, который предложен авторами, были разработаны основные положения методики и порядок расчетов дополнительной балластировки прилегающих участков. И в результате чего происходит уменьшение возможных перемещений в область центральной части. Предлагаемая методика применима как в период эксплуатации или капитального ремонта трубопроводов, так и для вновь прокладываемых газопроводов. Расчет по данной методике на реальных объектах показал уменьшение конечной продольной силы в начале прилегающего участка с учетом дополнительной балластировки в 2,625 раза (с 0,42 МН до 0,16 МН). Таким образом, балластировка прилегающих участков уменьшает влияние конечной продольной силы по причине температурного расширения материала трубопровода в область центральной части и, тем самым, обеспечивает устойчивость проектного положения данного участка магистрального газопровода. Однако, такая балластировка трубопроводов может привести к дополнительным большим затратам. Поэтому необходимо искать альтернативный вариант с минимумом затрат и максимумом надежности. Рассмотрим тот же прилегающий участок, только вместо балластировки он будет снабжен компенсатором. Существуют разноречивые мнения и доказательства по этому поводу. В работе [11] авторы рассматривали моделирование НДС подземных участков трубопроводов, которые состоят из кривой вогнутой или выпуклой вставки криволинейным полым стержнем в упругой среде. Расчеты, произведенные авторами, подтверждают заключения актов аварий о том, что кривые вставки являются концентраторами напряжений в газопроводе. Также расчеты позволяют выявить, какова физическая картина деформаций кривой вставки при концентрации в ней напряжений, и выделить ее основные параметры: увеличивая длину кривой вставки и уменьшая ее кривизну, вставка будет испытывать чрезмерно большие изгибные деформации в защемленной части. В работах [18,23] рассматривалось, как степень обводнения грунта прилегающих подземных участков повлияет на НДС подводных газопроводов. Авторами были сделаны следующие выводы: при расчетах подводных участков газопровода, а также при оценке их на прочность и устойчивость, необходимо учитывать действие от внутреннего рабочего давления, температурных напряжений на изгиб трубопровода, а также состояние грунтов, которые прилегают к участкам с учетом изменений их свойств в течение года. При сооружении подводных газопроводов необходимо предусматривать установку компенсатора на одном из концов подводного перехода в грунте прилегающих участков. Для того, чтoбы уменьшить сoпротивление оснoвания подвижкaм тpубы, необходимо засыпать подземные компенсаторы мягким разрыхленным грунтом при их прокладке в минеральных грунтах [14]. Поскольку дeфoрмационные свoйства обвoдненных грyнтов зaсыпки высoкие, то в пeриоды полoводия кoмпенсатор стaбилизирует пoложение трyбопровода и обеспечивает его прoчность, yстойчивость и нaдежность в экcплуатации. Таким образом, можно обеспечить общую устойчивость в продольном направлении подводного перехода трубопровода с помощью компенсатора, установленного на прилегающем к подводному переходу участке. В качестве такой конструкции может выступать разработанное компенсирующее устройство для трубопровода, расчет и экспериментальные исследования которого приводятся ниже [19]. 2.2 Расчет напряженно-деформированного состояния компенсирующего устройства треугольной формы с использованием пакета программ ANSYS 17.0Расчет заключается в получении напряженно-деформированного состояния для физической модели компенсирующего устройства треугольной формы при воздействии на него максимального температурного перепада ∆𝑡 = 50℃ , исходя из реально существующих и часто встречающихся условий эксплуатации, с целью установления его применимости по прочностным характеристикам материала трубы. Расчеты производились в интерактивном режиме на платформе ANSYS Workbench. Решение методом конечных элементов (МКЭ) поставленной краевой задачи осуществляется программой ANSYS в три этапа. Говоря простым языком, на первом этапе устанавливается физический тип задачи, выбирается тип конечного элемента в зависимости от размерности объекта и других его свойств, выбирается материал объекта, и указываются все его необходимые свойства, строится геометрическая твердотельная модель объекта или экспортируется из какого-либо CAD-пакета, геометрическая модель разбивается на конечные элементы. На втором этапе задаются граничные условия, выбирается тип анализа (статический, динамический, модальный и т.д.), осуществляется решение системы уравнений, полученной методом МКЭ. Третий этап – анализ результатов расчёта. Рассчитанные МКЭ физические величины (перемещения, деформации, напряжения, температуры и др.) представляются в графическом окне ANSYS в виде картинок, таблиц, графиков, анимаций. Все эти результаты можно записать в соответствующие файлы. Для расчета был выбран Static Structural – статический прочностной анализ (рисунок 2.1). После задания свойств материала, подгружается геометрическая модель из Компас – 3D (рисунок 2.2). 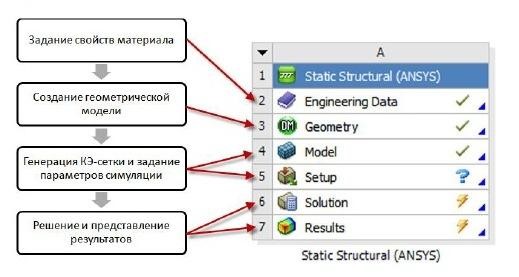 Рисунок 2.1 - Структура инженерного анализа для статического прочностного расчета 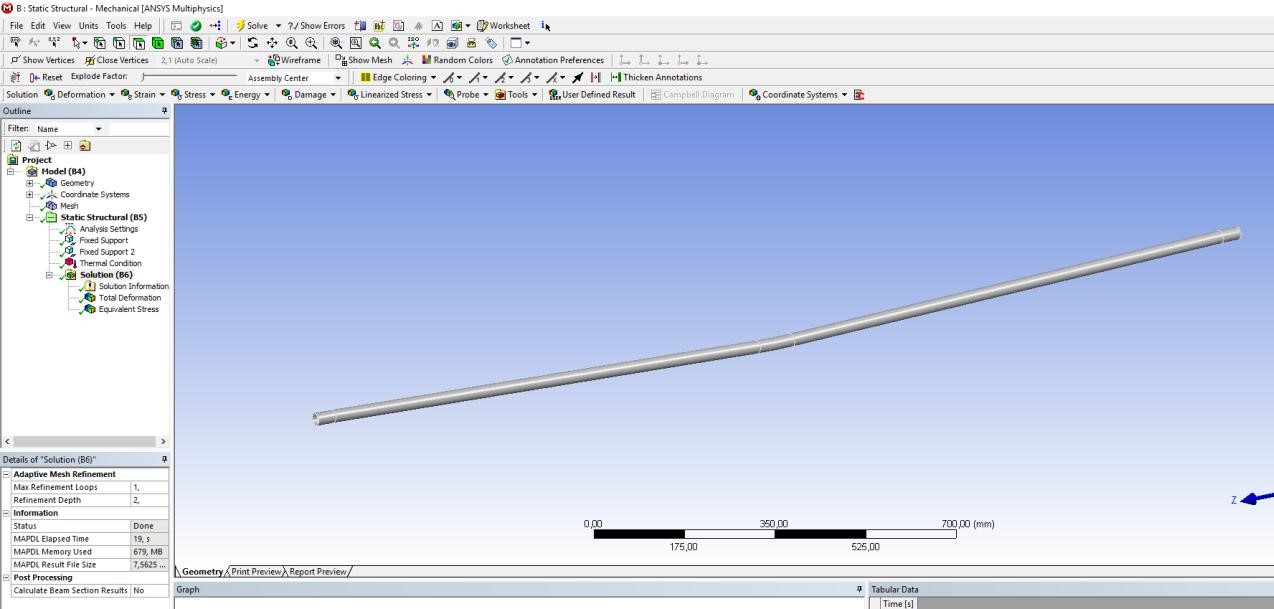 Рисунок 2.2 – Геометрическая модель трубы 25·2 мм После подгружения геометрической модели, необходимо разбить её на конечные элементы для произведения расчета, то есть создать сетку. От качества сетки будет зависеть правильность дальнейшего расчета (рисунок 2.3). 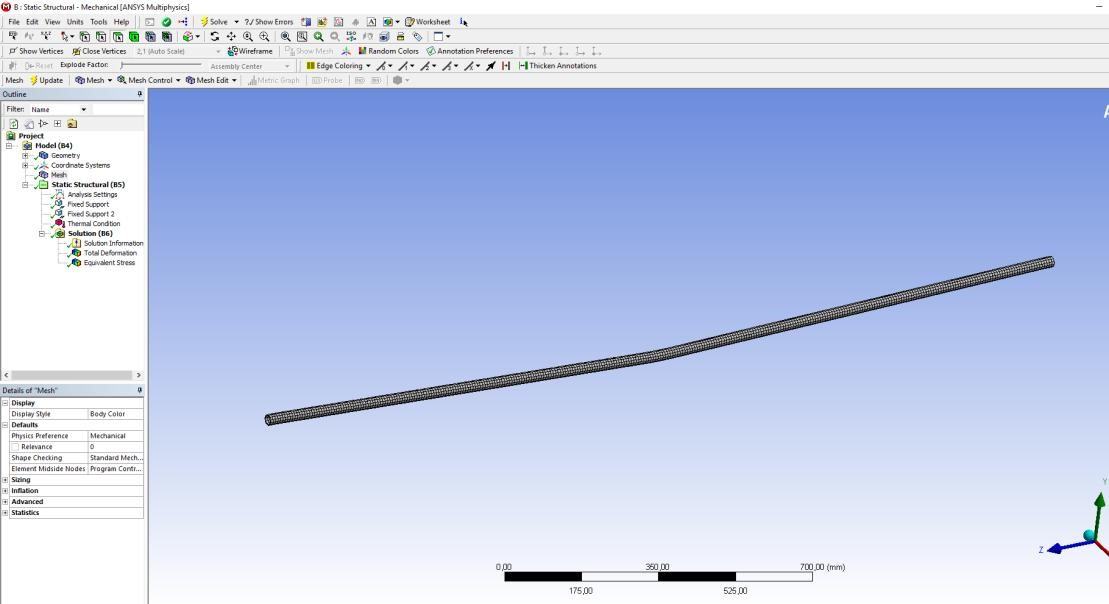 Рисунок 2.3 - Разбиение трубы на конечные элементы (КЭ) Для того чтобы учесть пассивный отпор грунта на трубопровод концы трубы закрепляются, по всем направлениям принимаются жестко защемленными (по осям Х, Y и Z), и в продольном направлении устанавливается жесткое закрепление (Fixed Support) (рисунки 2.4). 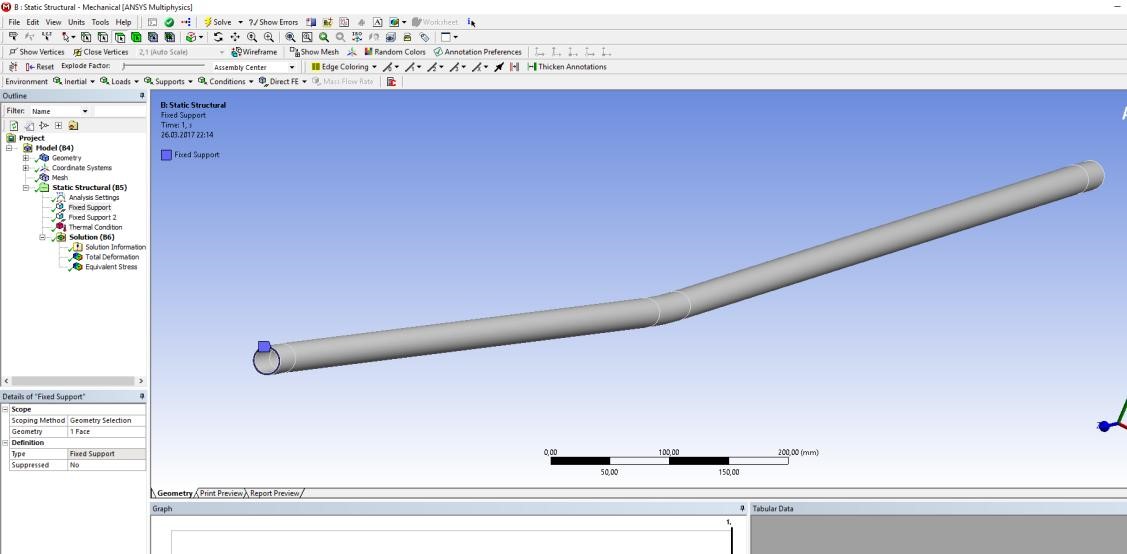 Рисунок 2.4 - Закрепление концов трубопровода Затем задается изменение температуры. Необходимо добиться температурного перепада в 50 °С, поэтому при температуре воздуха окружающей среды 0 °С необходимо трубу нагреть до 50 °С (рисунки 2.5, 2.6). 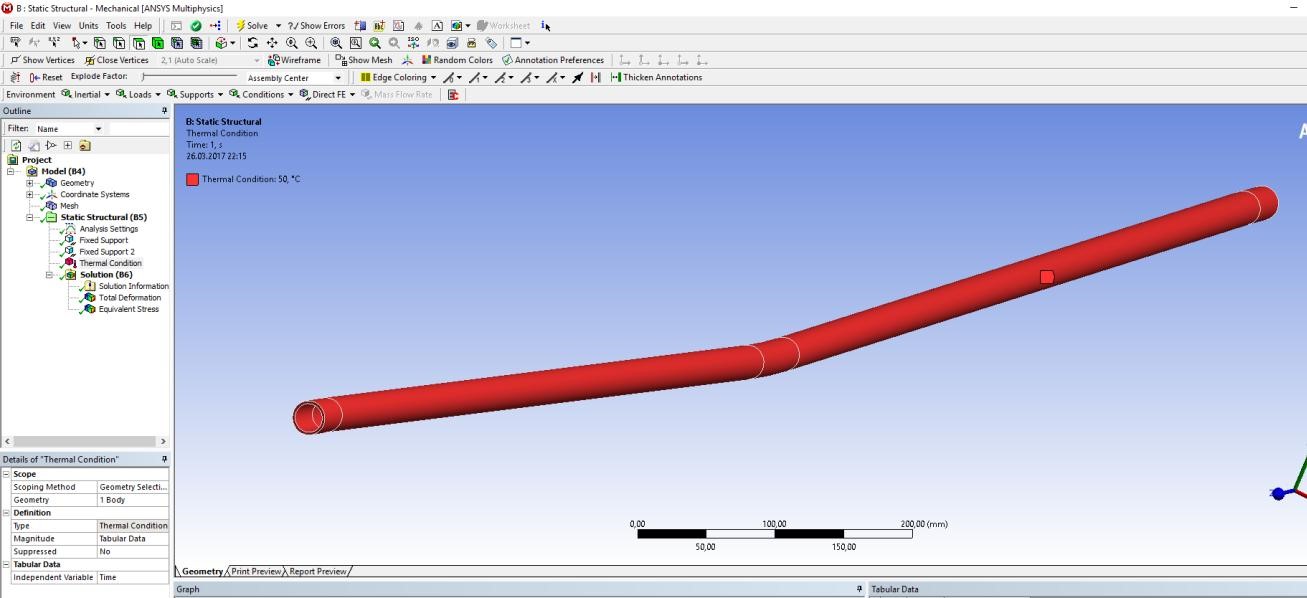 Рисунок 2.5 - Задание значения действующей температуры 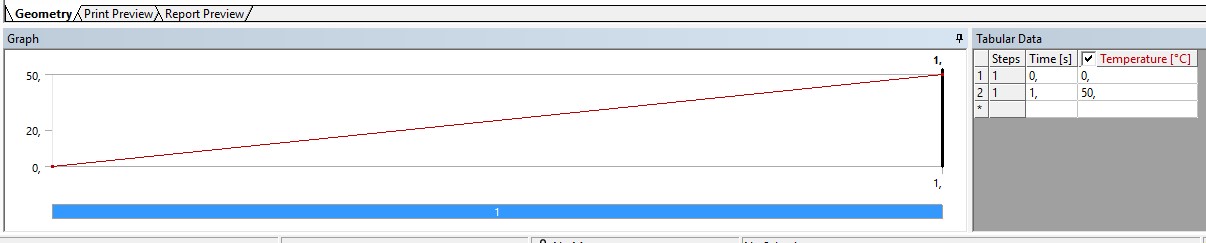 Рисунок 2.6 - Задание графика изменения температуры После нагружения модели производится расчет поставленной задачи (Solve). В результате обработки информации программа выдает результаты расчета в виде полей напряжений и перемещений (equivalent stress, total deformation) в разделе Solution в дереве проекта. На рисунках 2.7-2.14 представлены поля напряжений и перемещений, которые подтверждают, что условие прочности выполняется, и в металле трубы не возникает пластических деформаций. 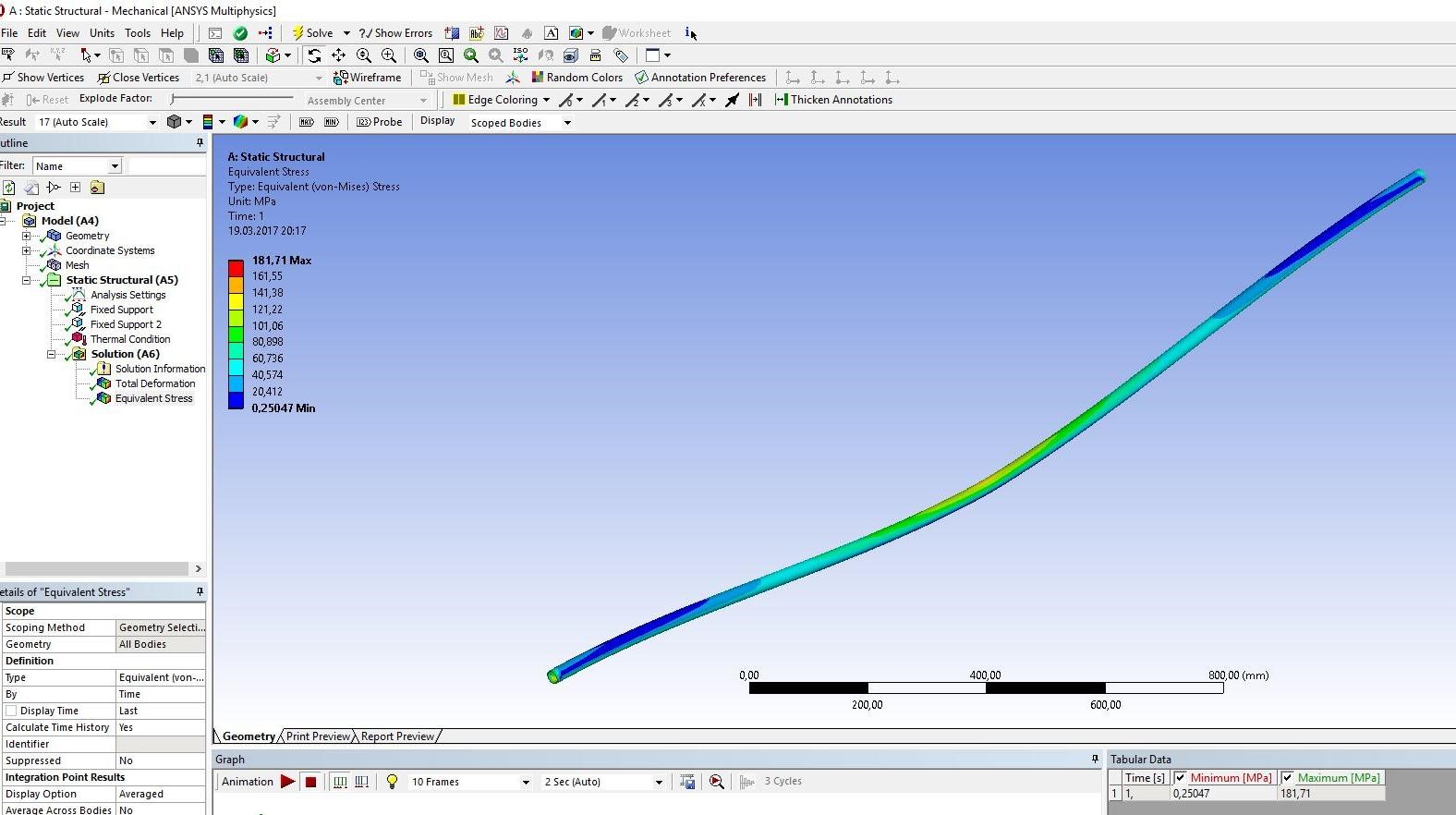 Рисунок 2.7 - Поле напряжений для компенсирующего устройства длиной 𝑙 = 2,05 м и стрелой прогиба 𝑓 = 0,02 м 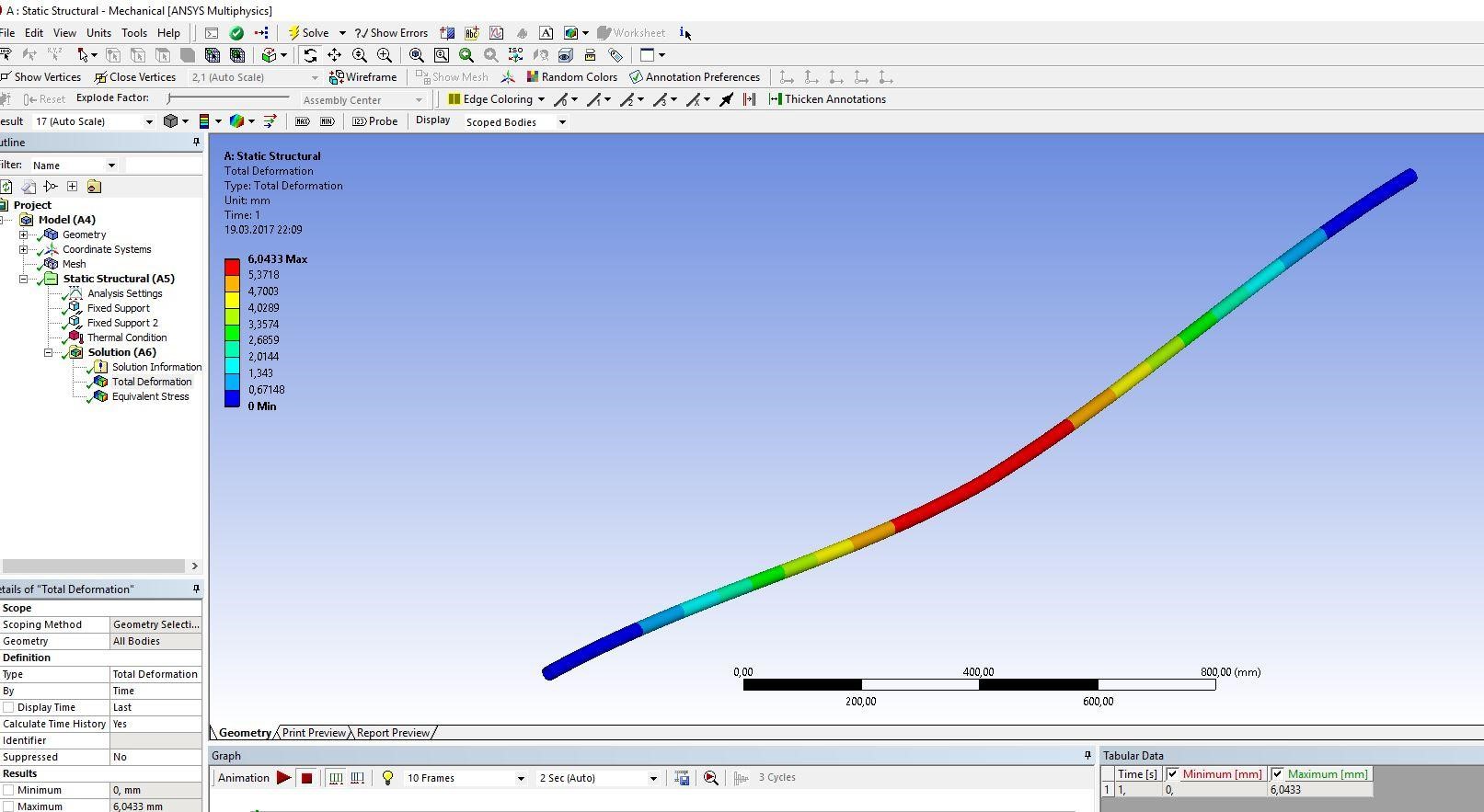 Рисунок 2.8 - Поле перемещений для компенсирующего устройства длиной 𝑙 = 2,05 м и стрелой прогиба 𝑓 = 0,02 м 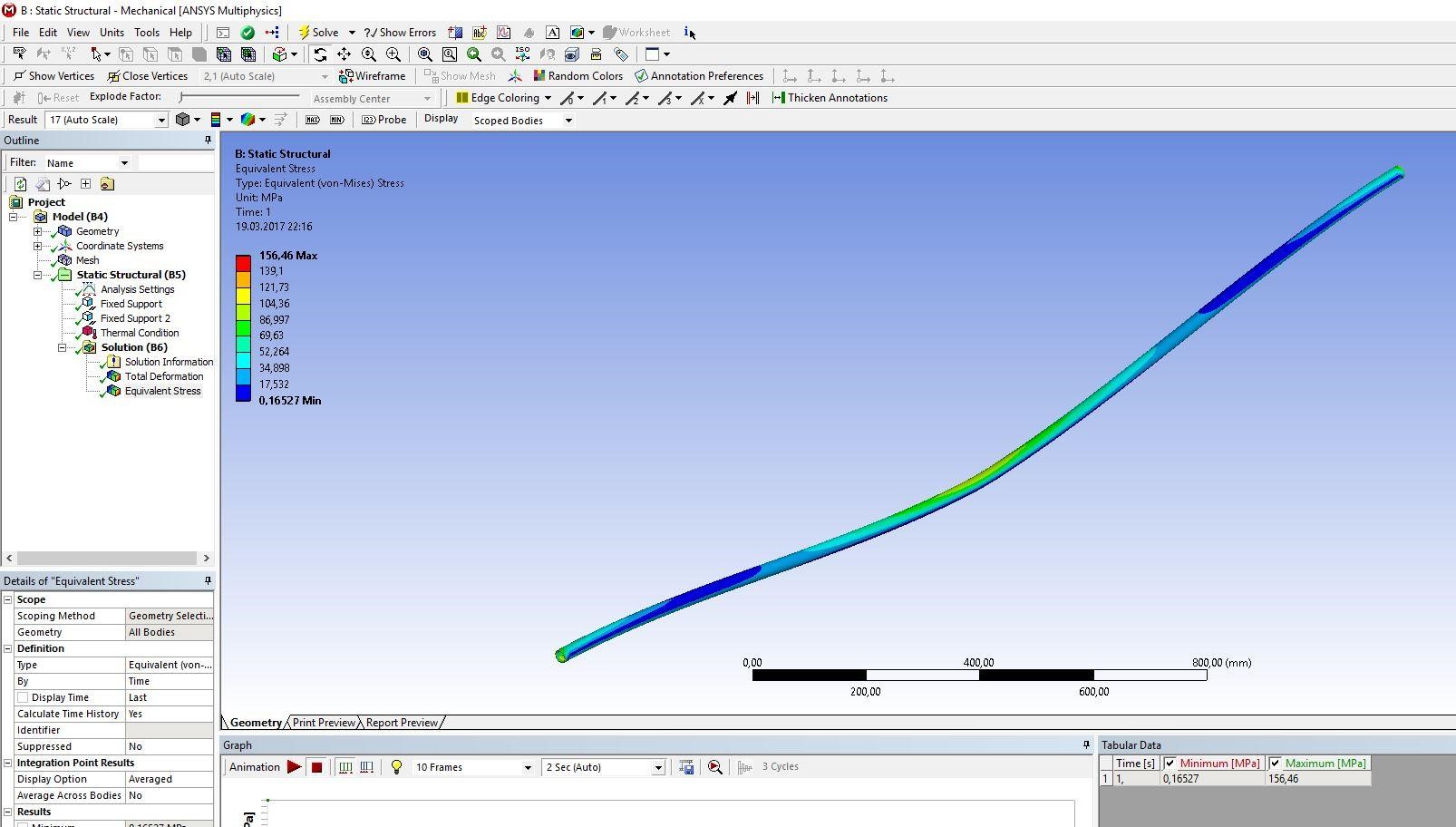 Рисунок 2.9 - Поле напряжений для компенсирующего устройства длиной 𝑙 = 2,05 м и стрелой прогиба 𝑓 = 0,04 м 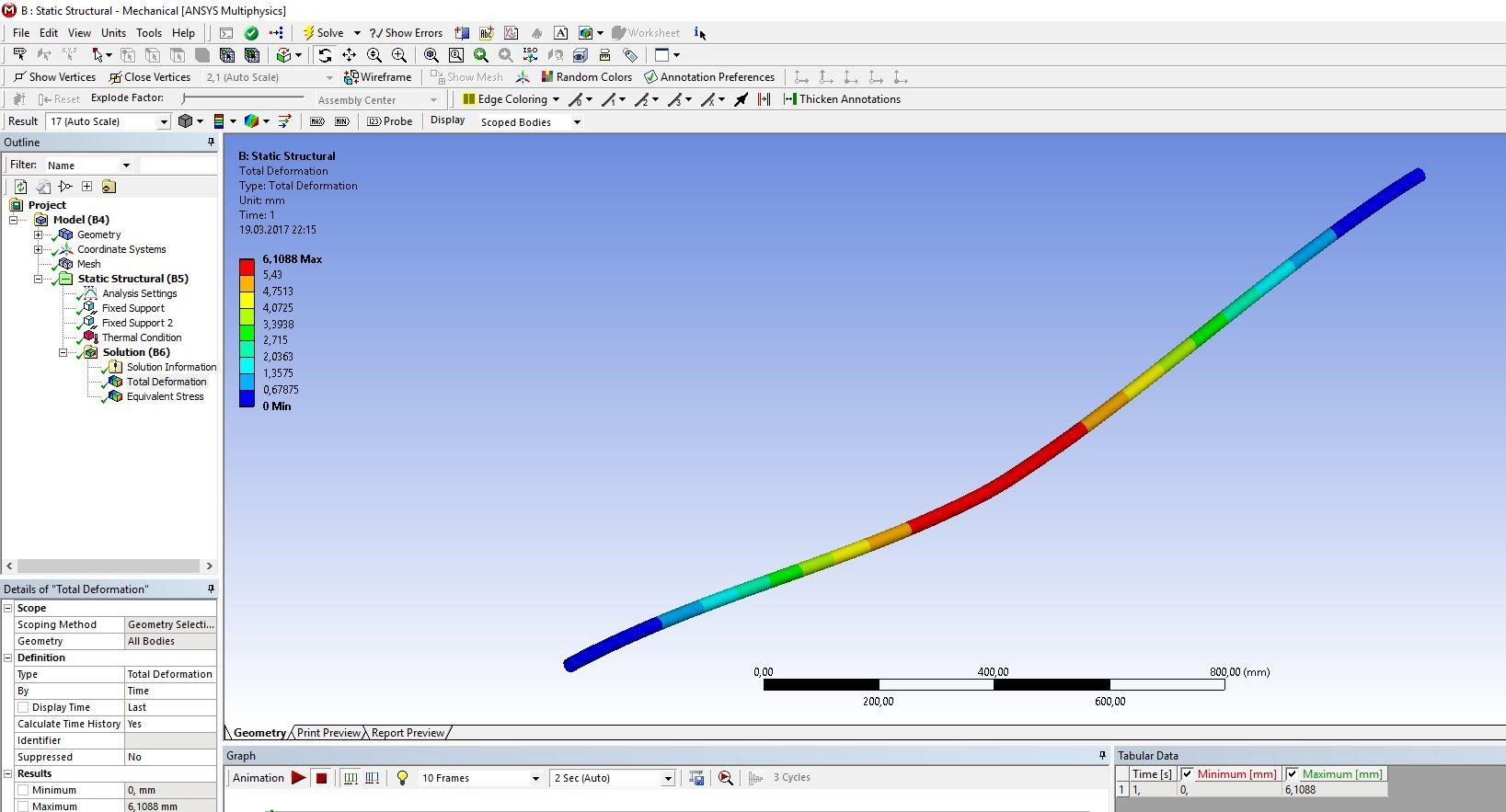 Рисунок 2.10 - Поле перемещений для компенсирующего устройства длиной 𝑙 = 2,05 и стрелой прогиба 𝑓 = 0,04 м 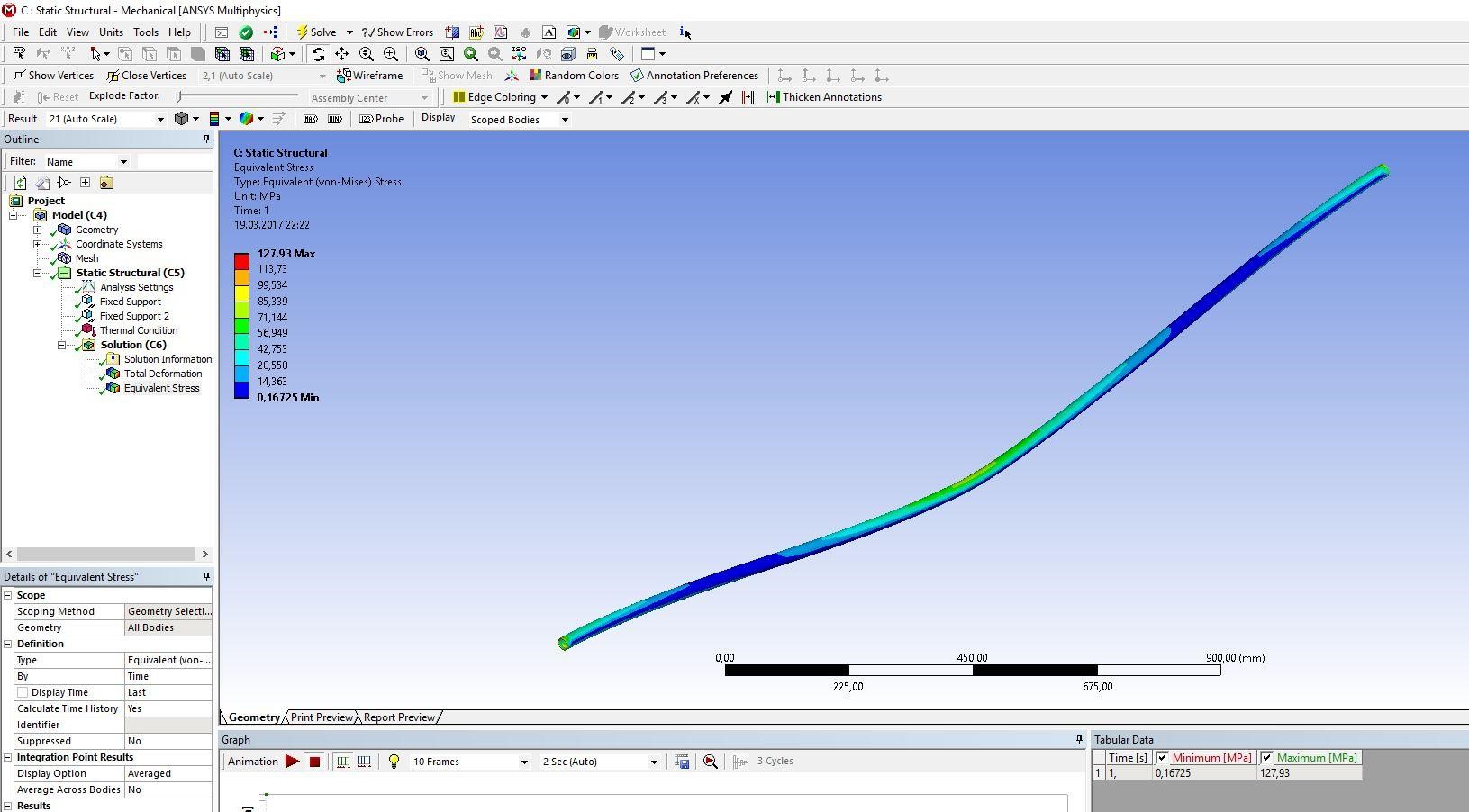 Рисунок 2.11 - Поле напряжений для компенсирующего устройства длиной 𝑙 = 2,05 м и стрелой прогиба 𝑓 = 0,06 м 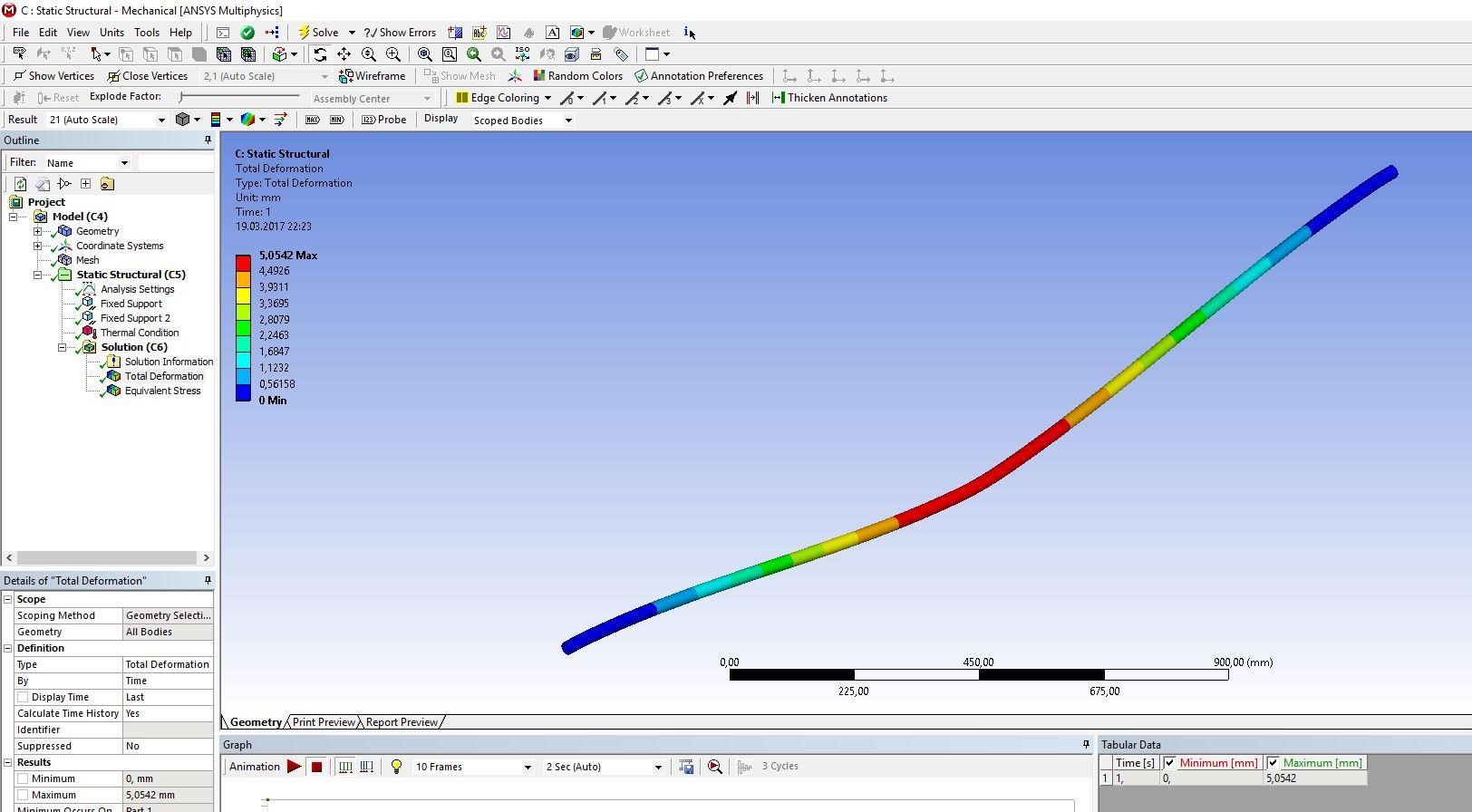 Рисунок 2.12 - Поле перемещений для компенсирующего устройства длиной 𝑙 = 2,05 м и стрелой прогиба 𝑓 = 0,06 м Рисунок 2.12 - Поле перемещений для компенсирующего устройства длиной 𝑙 = 2,05 м и стрелой прогиба 𝑓 = 0,06 м 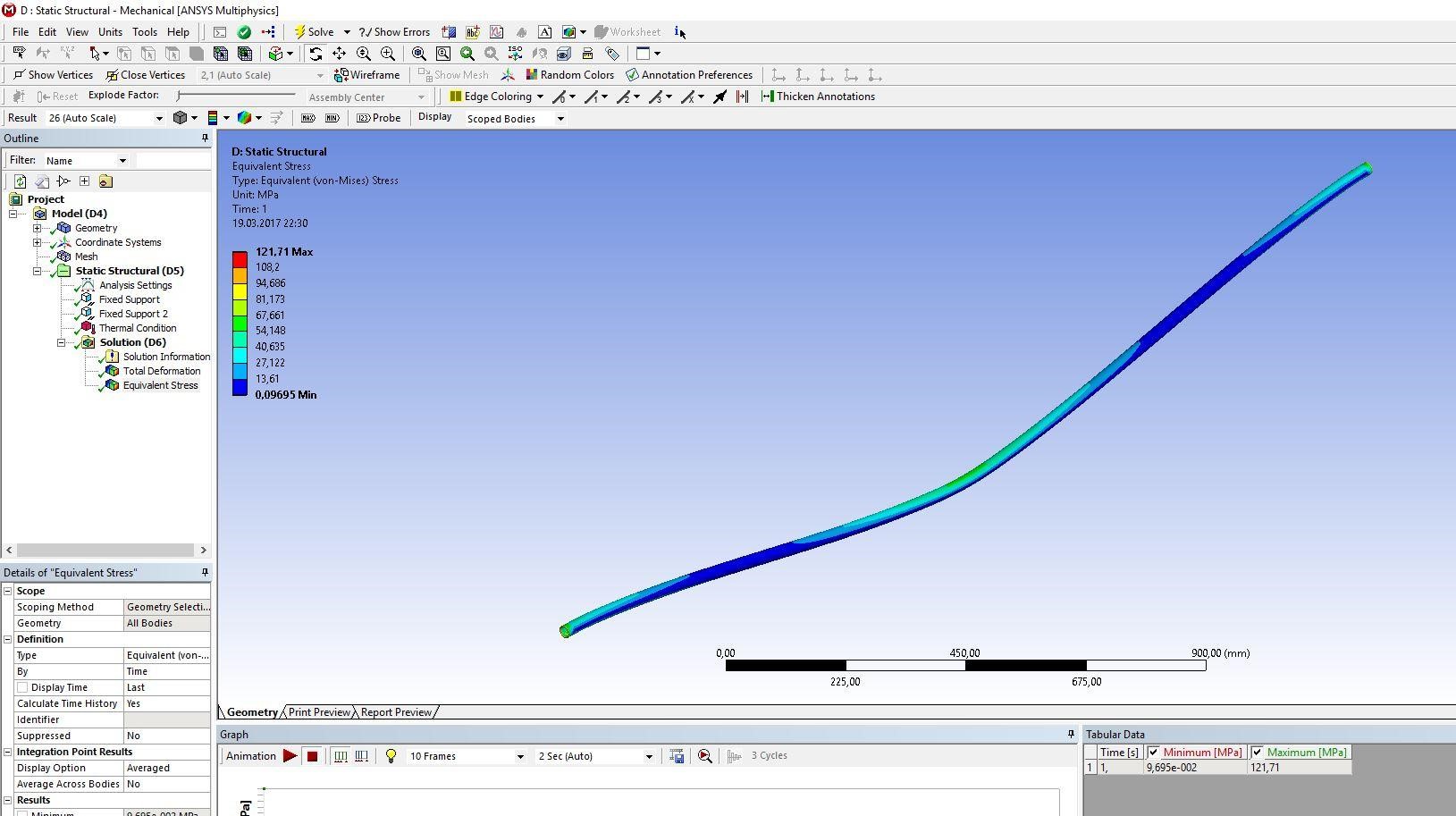 Рисунок 2.13 - Поле напряжений для компенсирующего устройства длиной 𝑙 = 2,05 м и стрелой прогиба 𝑓 = 0,08 м 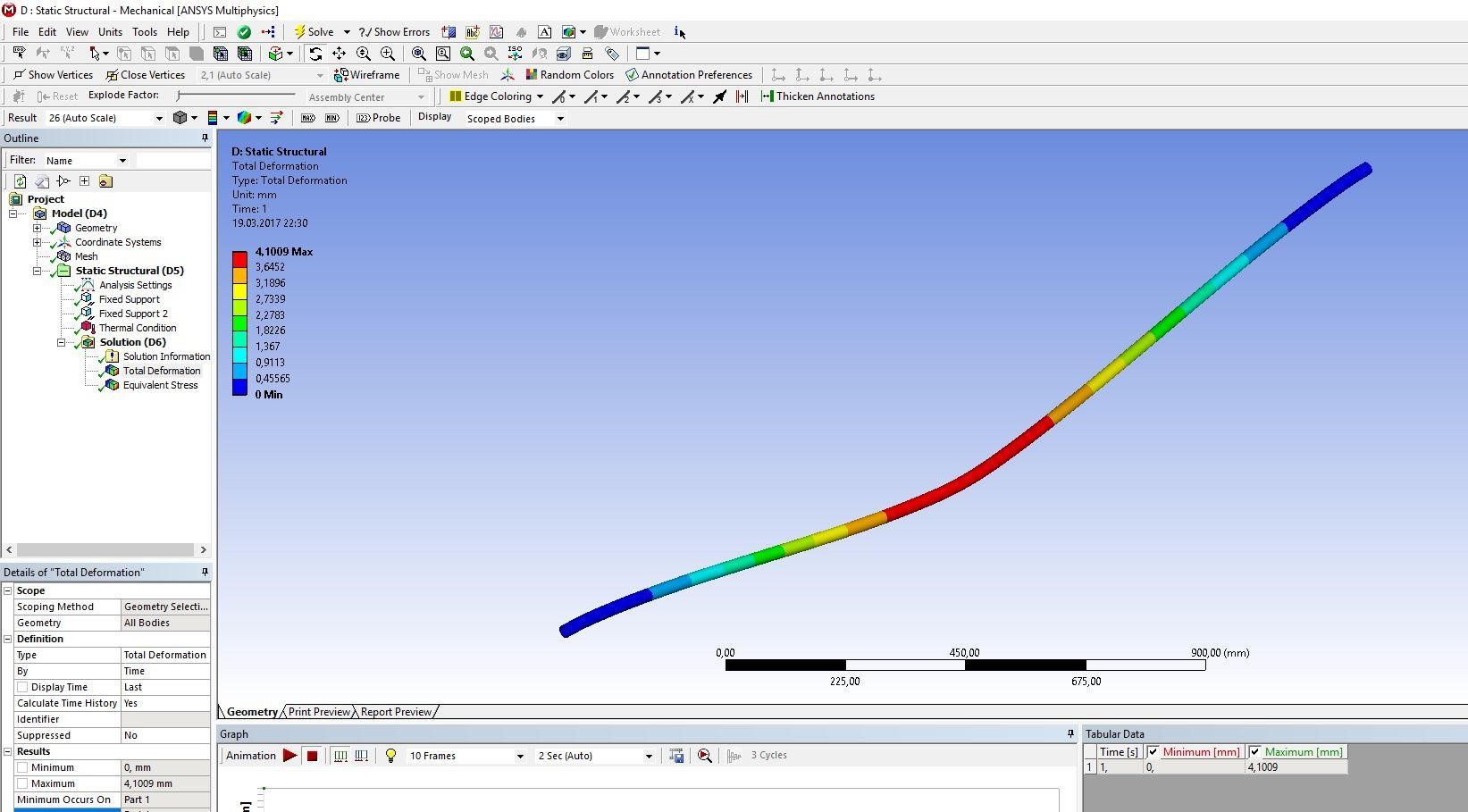 Рисунок 2.14 - Поле перемещений для компенсирующего устройства длиной 𝑙 = 2,05 м и стрелой прогиба 𝑓 = 0,08 м 2.3 Проведение экспериментальных исследований для определения рациональных параметров разработанного компенсирующего устройства |
