лекция. Теория графов. Решение задач. Лекция Курбанова И.Н. История возникновения теории графов

• Название: История возникновения теории графов
• Анкор: лекция
• Дата: 07.09.2022
• Размер: 0.56 Mb.
• Имя файла: Теория графов. Решение задач. Лекция Курбанова И.Н.docx
• Тип: Задача; #666922
• страница: 3 из 5

Представление графов в памяти

Чтобы решать задачи, связанные с графами, нужно сначала научиться сохранять его в памяти, а ещё лучше — сохранять оптимально. Существует несколько способов сделать это, и для каждой конкретной задачи оптимальным будет свой способ.

Матрица смежности

Самый простой способ сохранить граф в памяти — матрица смежности. Нарисуем таблицу, которая чем-то напоминает таблицу умножения: в первой строчке и в первом столбце будут стоять номера (или любые названия) вершин, а на пересечении столбца и строки будем ставить, например, 1 если между этими вершинами есть ребро и 0 если нет. Кроме 1 и 0 можно ставить, например, вес ребра, а для обозначения отсутствия ребра — просто очень большое число. Какой именно вариант использовать, зависит от каждой конкретной задачи. Также задача определяет, что ставить на диагонали получившейся матрицы.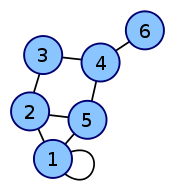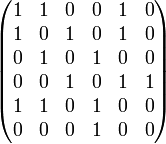



Граф и его матрица смежности.

Матрица смежности элементарно реализуется в большинстве языков программирования, достаточно лишь объявить двумерный массив.

Другие способы

Существуют и другие способы хранения графа в памяти, например, матрица инцидентости, которая удобна при использовании методов линейной алгебры в задачах на графах, или списки рёбер, но практическое применение в задачах обычно находят описанные выше два способа.

Основные задачи теории графов

Обходы графа

Часто требуется обойти все вершины графа в определённом порядке, например, для проверки его на связность или упорядочения задач при планировании (топологическая сортировка графа). Существует два стандартных метода обхода графа — обход в глубину и обход в ширину.

Обход в глубину (DFS)

Обход в глубину можно описать так: представьте, что вы в лабиринте. Идите всегда прямо, а на всех развилках выбирайте самый левый путь. Упёршись в тупик, возвращайтесь обратно до последней развилки и выбирайте следующий путь слева. Продолжайте, пока не обойдёте весь лабиринт.

Обход в ширину (BFS)

Обход в ширину можно наглядно представить себе так: в какой-то стартовой точке лабиринта разливается жидкость, и она начинает равномерно заполнять все его помещения, продвигаясь все дальше. При этом в каждый момент времени все точки края разливающейся воды находятся на одном расстоянии от начала.

Этот обход, как и обход DFS, можно применять для поиска путей в графах. Основное его отличие в том, что поиск не уходит сразу далеко от начала, а продвигается вглубь графа постепенно, неким «фронтом».

Его реализация немного сложнее, чем DFS. Для этого нам понадобится такая структура данных, как очередь. Очередь, как видно из названия, моделирует обычную очередь в магазине. Обычно это список, в которой можно класть элементы с одной стороны, а забирать — с другой. Обход в ширину хранит в очереди вершины, которые еще предстоит просмотреть.

Другие задачи

Другими классическими задачами теории графов являются, например, задача топологической сортировки и задача поиска наименьшего остовного дерева.

Проблема четырёх красок

Проблема четырёх красок — математическая задача, предложенная Гутри в 1852 году.

Выяснить, можно ли всякую расположенную на сфере карту раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета.

Иначе говоря, показать что хроматическое число плоского графа не превосходит 4.

О доказательстве

К. Аппель и В. Хакен доказали в 1976 г., что так можно раскрасить любую карту. Это была первая крупная математическая теорема, для доказательства которой был применён компьютер. Несмотря на последующие упрощения, доказательство практически невозможно проверить, не используя компьютер. Поэтому некоторые математики отнеслись к этому доказательству с недоверием, что объяснялось не только использованием компьютера, но и громоздкостью описания алгоритма первых доказательств (741 страница), впоследствии были предложены более компактные алгоритмы и скорректирован ряд ошибок. Проблема четырех красок является одним из известнейших прецедентов неклассического доказательства в современной математике.

Исторически планарные графы связаны с одной знаменитой задачей.

Задача о домиках и колодцах. В некоторой деревне есть три колодца. Трое жителей, живущие в трех стоящих рядом домиках перессорились, и решили так протоптать тропинки от своих домов к каждому из трех колодцев, чтобы они не пересекались. Удастся ли им выполнить свой план?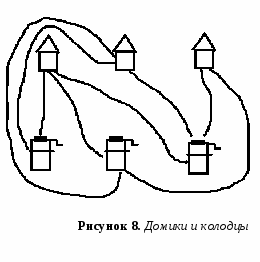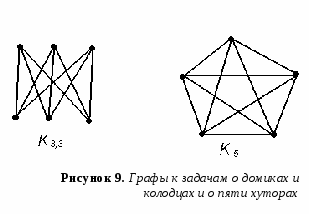





Решим эту задачу. Проведем тропинки так, как это показано на рисунке 8. Как видно, нам удалось провести только восемь тропинок, а девятая должна пересечься хотя бы с одной. Можно доказать (мы не будем приводить строгое доказательство), что эта задача не имеет решения. Дело в том, что по мере проведения тропинок из двух первых домиков, будет получаться некоторый замкнутый контур, внутри которого будет стоять один из колодцев, при этом третий домик будет находиться снаружи от этого контура. Для того чтобы соединить этот домик с колодцем, обязательно потребуется пересечь новой тропинкой одну из уже проложенных.

Задача о четырех красках. На политической карте мира нарисовано несколько государств. Карту нужно раскрасить так, что бы две страны, имеющие общую границу, были покрашены в разные цвета.

В классическом варианте предполагалось, что карту можно раскрасить четырьмя цветами. Покажем, как эта задача связана с графами. Обозначим каждую страну на карте точкой, вершины, отвечающие странам, имеющим общую границу, соединим ребрами. Теперь задачу о раскрашивании можно сформулировать так: раскрасить вершины планарного графа так, чтобы любые две смежные были покрашены в разные цвета. Эта задача может быть решена для графов с малым количеством вершин. Если же число вершин достаточно велико, то гипотеза четырех красок оказывается неверной. (Этот факт установлен с помощью мощных компьютеров.)

Вместе с тем, довольно простыми средствами была доказана теорема о пяти красках.

Теорема. Планарный граф можно раскрасить пятью красками так, что любые смежные вершины будут окрашены в разные цвета.

Еще одна интересная проблема: сколькими способами можно раскрасить граф, если имеется n красок.

Оказывается, что число способов раскрашивания является многочленом от n, коэффициенты этого многочлена можно вычислить с помощью специального алгоритма.

Укажем еще одно обобщение задачи о раскрасках. Известно, что граф без самопересечений располагается на некоторой поверхности (на сфере, на торе, на бутылке Клейна и т.п.), какое минимальное количество красок нужно для его раскрашивания?

Ответ на этот вопрос был получен в разделе математики, называющемся «топологией». Оказалось, что для всех замкнутых двумерных поверхностей (кроме сферы), данное число выражается через Эйлерову характеристику этой поверхности.