лекция. Теория графов. Решение задач. Лекция Курбанова И.Н. История возникновения теории графов
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
Дополнительная нформация о графеПутем или цепью в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром. Циклом называют путь, в котором первая и последняя вершины совпадают. Путь или цикл называют простым, если ребра в нем не повторяются. Если в графе любые две вершины соединены путем, то такой граф называется связным. Можно рассмотреть такое подмножество вершин графа, что каждые две вершины этого подмножества соединены путем, а никакая другая вершина не соединена ни с какой вершиной этого подмножества. Каждое такое подмножество, вместе со всеми ребрами исходного графа, соединяющими вершины этого подмножества, называется компонентой связности. Один и тот же граф можно нарисовать разными способами. Вот, например, два изображения одного и того же графа, которые различаются кривизной: 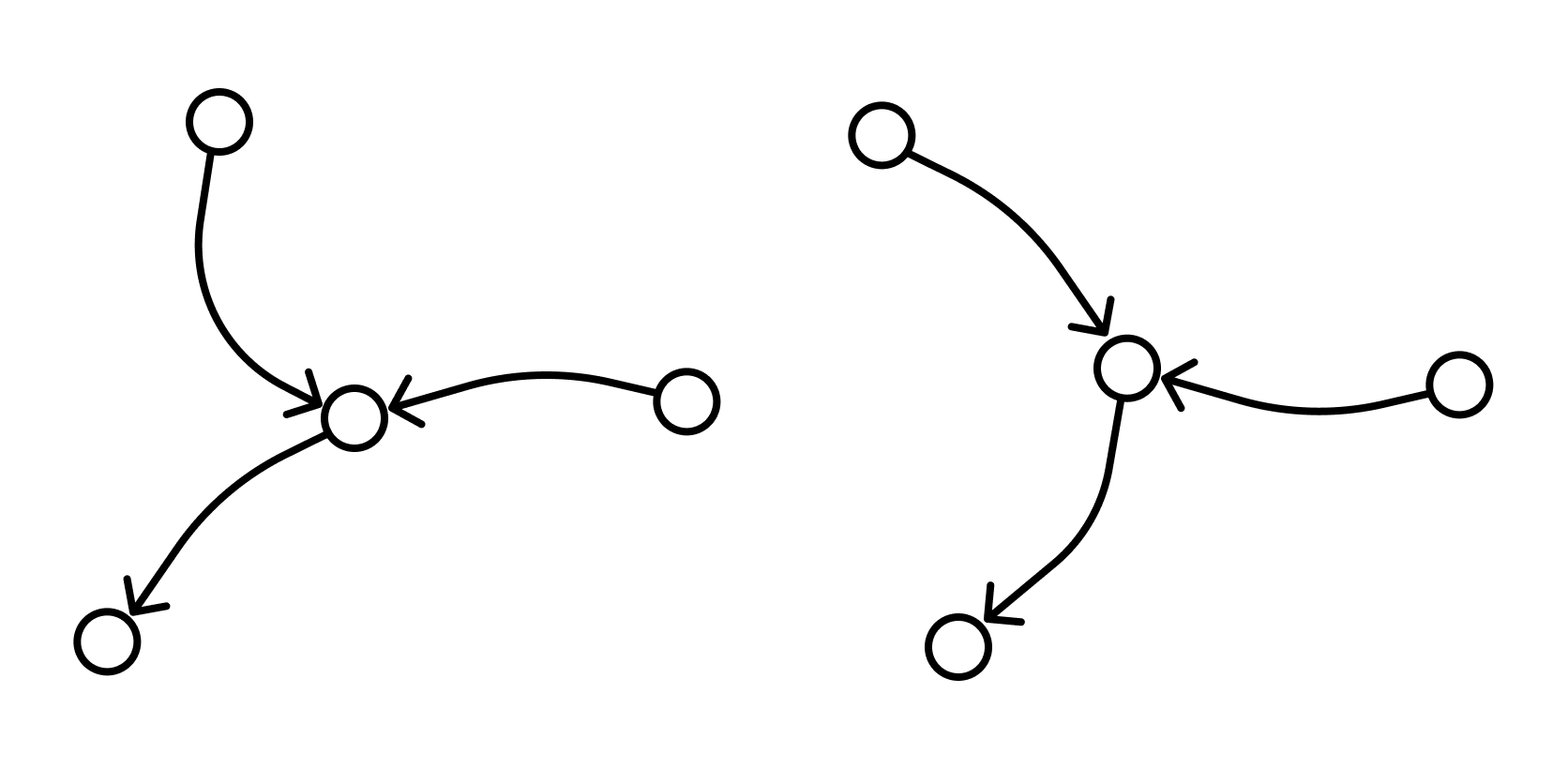 Два графа называются изоморфными, если у них поровну вершин. При этом вершины каждого графа можно занумеровать числами так, чтобы вершины первого графа были соединены ребром тогда и только тогда, когда соединены ребром соответствующие занумерованные теми же числами вершины второго графа. Граф H, множество вершин V’ которого является подмножеством вершин V данного графа G и множество рёбер которого является подмножеством рёбер графа G соединяющими вершины из V’ называется подграфом графа G. Визуализация графовых моделейВизуализация — это процесс преобразования больших и сложных видов абстрактной информации в интуитивно-понятную визуальную форму. Другими словами, когда мы рисуем то, что нам непонятно — и сразу все встает на свои места. Графы — и есть помощники в этом деле. Они помогают представить любую информацию, которую можно промоделировать в виде объектов и связей между ними. Граф можно нарисовать на плоскости или в трехмерном пространстве. Его можно изобразить целиком, частично или иерархически. Изобразительное соглашение — одно из основных правил, которому должно удовлетворять изображение графа, чтобы быть допустимым. Например, при изображении блок-схемы программы можно использовать соглашение о том, что все вершины должны изображаться прямоугольниками, а дуги — ломаными линиями с вертикальными и горизонтальными звеньями. При этом, конкретный вид соглашения может быть достаточно сложен и включать много деталей. Виды изобразительных соглашений: 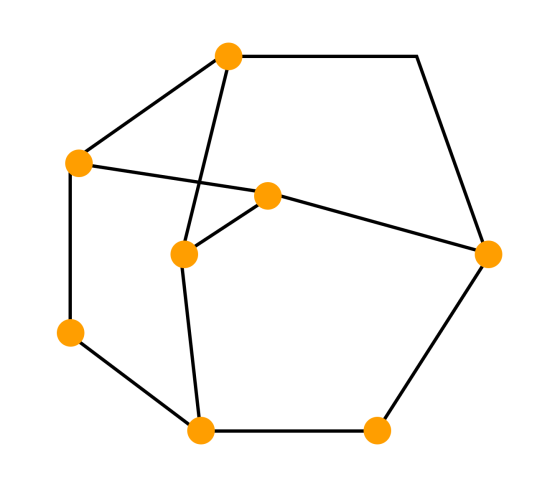 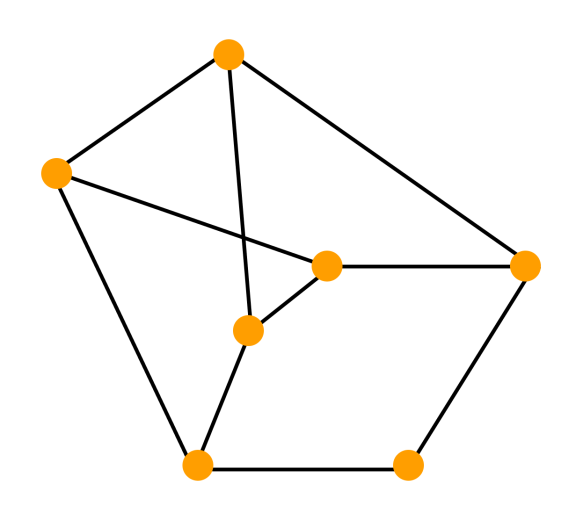 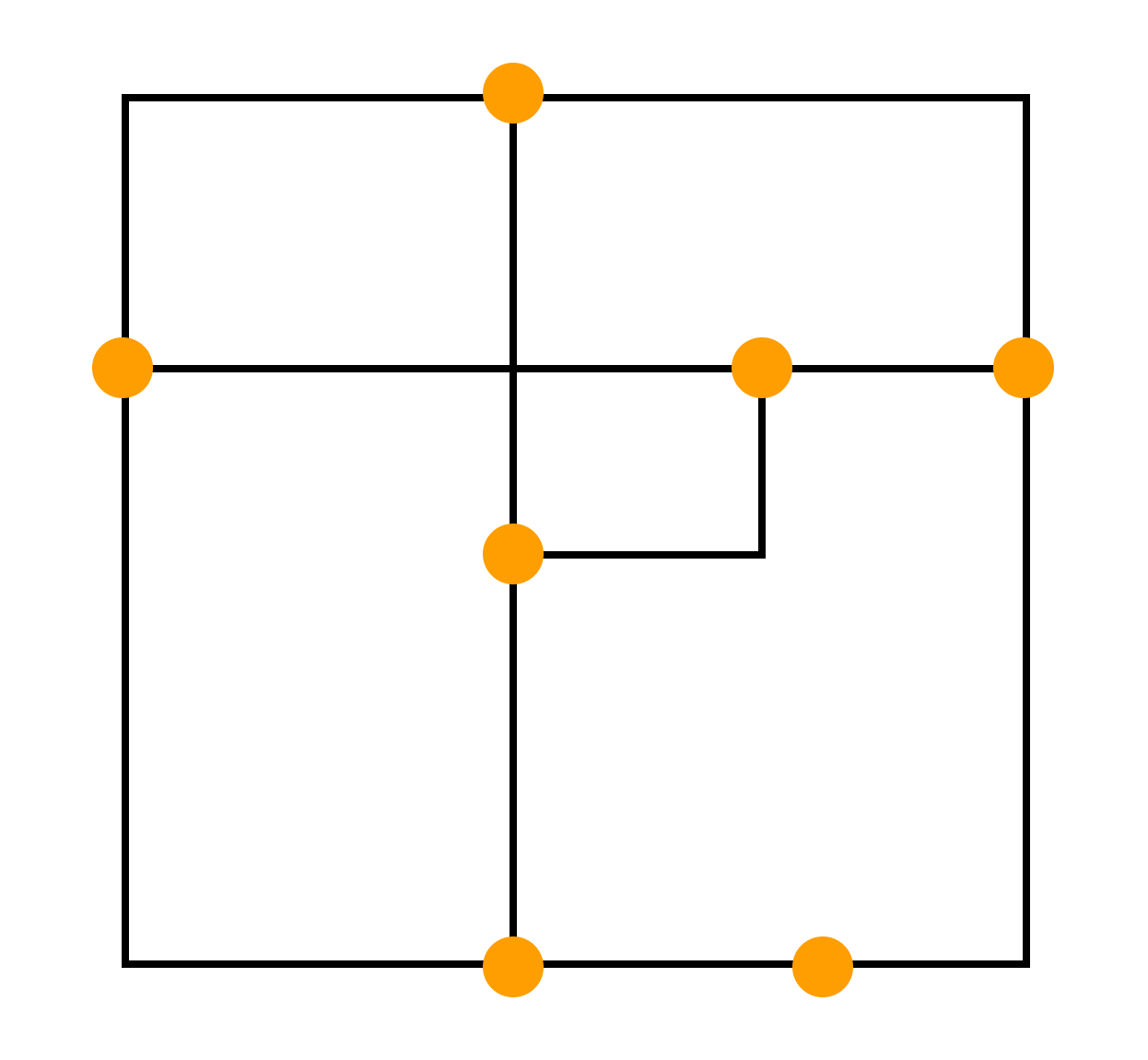 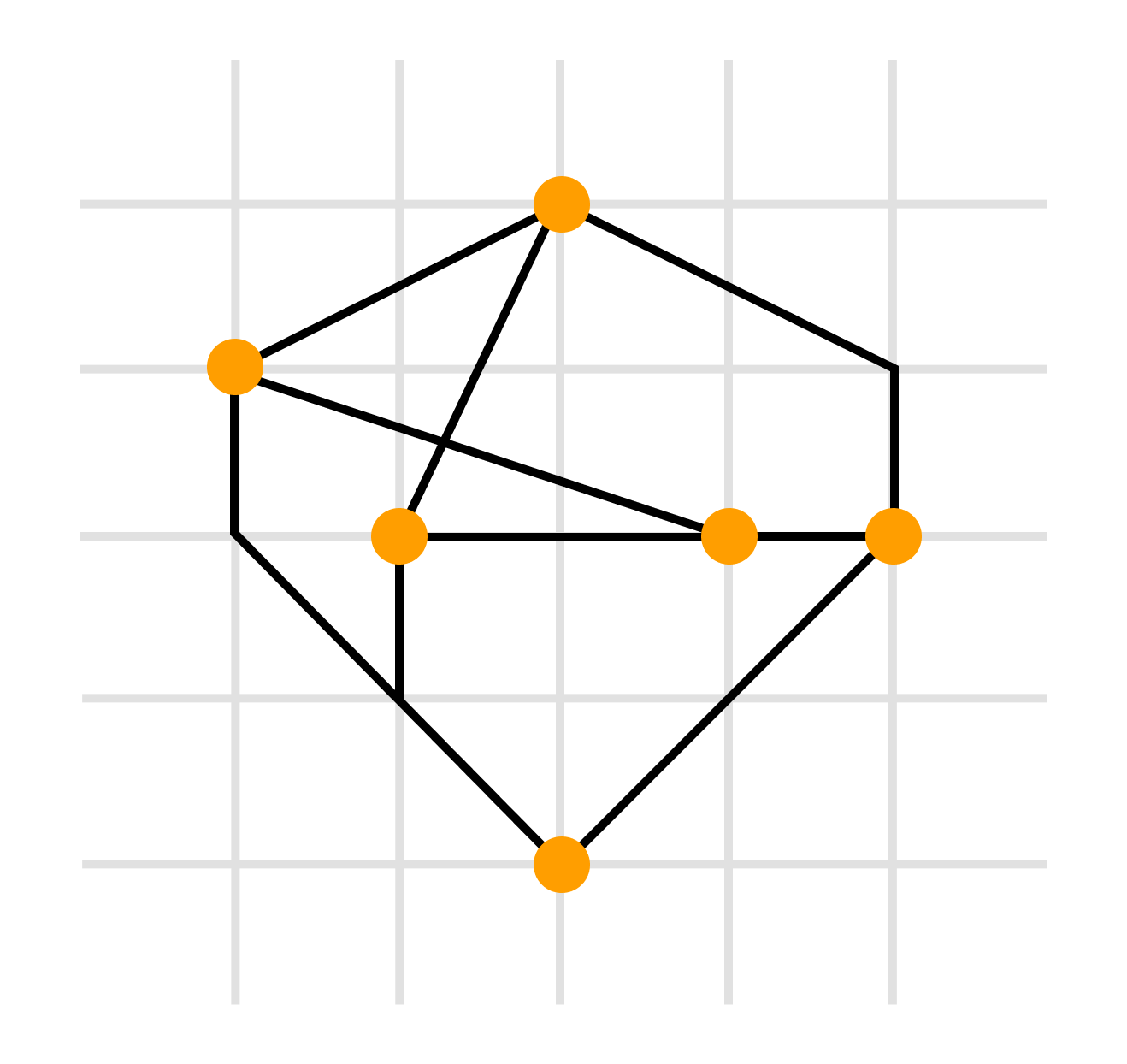 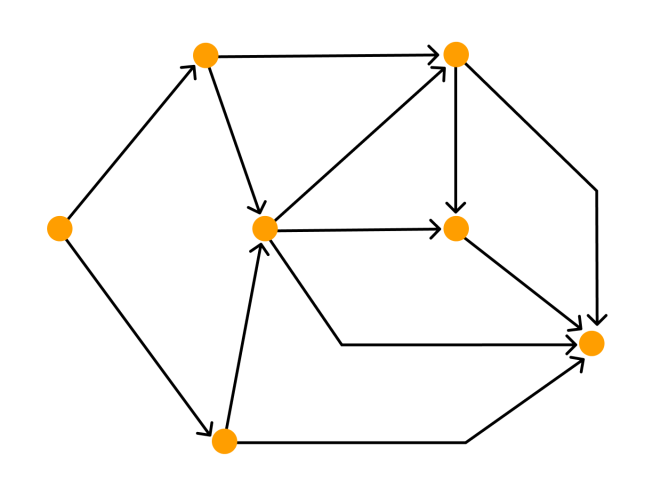 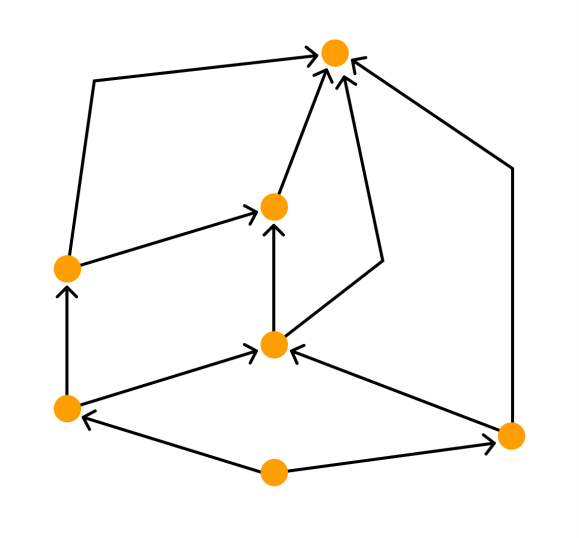 полилинейное изображение — каждое ребро графа рисуют в виде ломаной линии прямолинейное изображение — каждое ребро представляют с помощью отрезка прямой ортогональное изображение — каждое ребро графа изображается в виде ломаной линии, состоящей из чередующихся горизонтальных и вертикальных сегментов сетчатое изображение — все вершины, а также все точки пересечения и сгибы ребер имеют целочисленные координаты. То есть находятся в узлах координатной сетки, образованной прямыми, параллельными координатным осям и пересекающими их в точках с целочисленными координатами плоское изображение предполагает отсутствие точек пересечения у линий, изображающих ребра. восходящее или нисходящее изображение имеет смысл по отношению к ациклическому орграфу и предполагает, что каждая дуга изображается ориентированной линией, координаты точек которой монотонно изменяются в направлении снизу вверх или сверху вниз, а также слева направо |
