лекция. Теория графов. Решение задач. Лекция Курбанова И.Н. История возникновения теории графов
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
ВведениеТеория графов — раздел математики и информатики, нашедший широкое применение в современных прикладных задачах. В первую очередь, это задачи поиска маршрута на картах, но её применение не ограничивается навигационными приложениями. Графы возникают там, где между данными существуют какие-либо нелинейные связи. Например, это могут быть компьютеры, соединённые в сеть. Или же это могут быть задачи, которые надо выполнить в каком-то порядке, причём некоторые задачи надо выполнять строго после каких-то других. Существуют алгоритмы, позволяющие вычислить оптимальный порядок выполнения таких задач. История возникновения теории графовЛеонард Эйлер и задача о Кёнигсберских мостахРодоначальником теории графов считается Леонард Эйлер. В 1736 году в одном из своих писем он формулирует и предлагает решение задачи о семи кёнигсбергских мостах, ставшей впоследствии одной из классических задач теории графов. Издавна среди жителей Кёнигсберга (теперь Калининграда) была распространена такая загадка: как пройти по всем мостам, не проходя ни по одному из них дважды? Многие кёнигсбержцы пытались решить эту задачу как теоретически, так и практически, во время прогулок. Но никому это не удавалось, однако не удавалось и доказать, что это даже теоретически невозможно. В 1736 году задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук Леонарда Эйлера, о чём он написал в письме итальянскому математику и инженеру Мариони от 13 марта 1736 года. В этом письме Эйлер пишет о том, что он смог найти правило, пользуясь которым легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них (в случае семи мостов Кёнигсберга это невозможно). Для того, чтобы решить эту задачу, Эйлер сделал специальные обозначения. Каждую часть суши (остров или берег реки) он обозначил кружком на бумаге, а затем соединил линиями те кружки, между которыми существуют мосты. Такие обозначения подчеркивают, что в этой задаче фактическое расположение, форма, длина и другие свойства объектов не представляют интереса, важны только связи между ними. Такая картинка на бумаге или на экране компьютера называется графом. Кружки — это его вершины, а линии — рёбра. Размышляя над этой и другими картинками из кружков и линий, Эйлер пришел к следующим выводам о графах: Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно всегда быть чётно. То есть, просто не может существовать графа, который имел бы нечётное число нечётных вершин. Если все вершины графа чётные, то его можно начертить не отрывая карандаша от бумаги, при этом начинать можно с любой вершины графа и завершить его в ней же. Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком. (такой граф называют уникурсальным) Доказательство. Вначале заметим, что если все вершины графа имеют степень не меньше двух, то в нем существует хотя бы один цикл. Рассмотрим случай, когда все вершины четны. Применим «метод стирания». Выберем некоторую точку и начнем строить путь. Так как степени всех вершин четны, то они не меньше двух. Поэтому, войдя по некоторому ребру в данную точку, мы всегда можем выйти из нее по второму ребру. Будем отмечать пройденные вершины. Так как число вершин конечно, то на каком-то шаге мы перейдем в одну из уже отмеченных вершин и таким образом замкнем цикл. Теперь сотрем этот цикл (естественно, запомнив его где-то) и рассмотрим получившийся граф. Он может оказаться несвязным, но, тем не менее, все его вершины будут иметь четную степень. Применим к этому графу ту же процедуру, и будем это делать до тех пор, пока остается хотя бы один нетривиальный подграф. В результате мы получим несколько циклов, которые не имеют общих ребер, а все вместе образуют исходный граф. Нам остается только склеить эти циклы в один. Возьмем два цикла (…ВАС…) и (…НАМ…), имеющие общую вершину А, разрежем их в этой вершине и склеим по такому правилу: сначала выписываем вершины первого цикла, потом, дойдя до точки А, записываем все вершины второго цикла, а затем продолжаем выписывать оставшиеся вершины первого цикла. Очевидно, что в итоге у нас получится один цикл, который содержит все ребра исходного графа. Предположим теперь, что в исходном графе ровно две нечетных вершины А и В. Соединим их дополнительных ребром АВ, и получим граф, все вершины которого четны. Построим для него эйлеров цикл по указанному выше алгоритму. Перепишем его так, чтобы вершина А была начальной, а ребро АВ – последним. Удалив из этого цикла ребро АВ получим цикл, начинающийся в А и заканчивающийся в В. Этот путь проходит через все ребра исходного графа. Предположим теперь, что граф уникурсален. Докажем, что в нем не более двух нечетных вершин. Очевидно, что рисовать такой граф нужно, начиная с нечетной вершины. Причем завершить маршрут нужно в другой нечетной вершине. Если же имеется еще одна нечетная вершина, то она не может быть ни начальной, ни конечной. Поэтому, когда мы в нее заходим, то должны обязательно выйти. Каждый проход через вершину уменьшает число не пройденных ребер, связанных с этой вершиной, ровно на два. В итоге, на каком то шаге в нечетной вершине останется только одно не пройденное ребро, зайдя по которому в вершину мы уже не сможем из нее выйти. Теорема доказана полностью. Граф кёнигсбергских мостов имел четыре нечётные вершины (т.е. все), следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды. 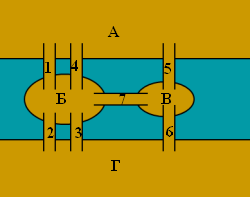 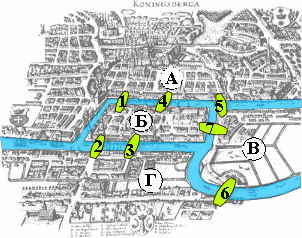 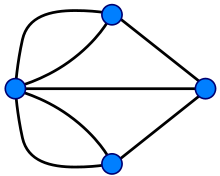 |
