лекция. Теория графов. Решение задач. Лекция Курбанова И.Н. История возникновения теории графов
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
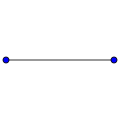
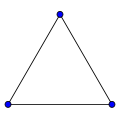
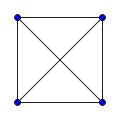
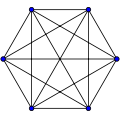
Определения теории графовГраф — конечное множество вершин, природа которых не важна, и конечно множество рёбер, соединяющих между собой какие-либо вершины. Графы могут быть ориентированными и неориентированными. Если в рамках задачи по рёбрам можно перемещаться в обоих направлениях, то граф называется неориентированным. Если же по каждому ребру можно пройти только в одну сторону, то граф ориентированный. В таком случае рёбра обычно обозначаются стрелками, а не просто линиями. 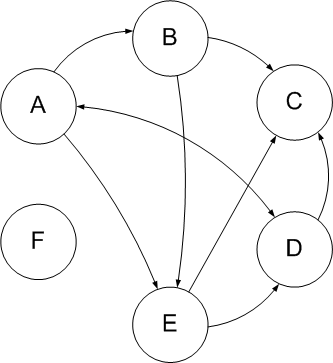 Пример ориентированного графа Иногда бывает полезно связать с ребрами графа какие-то числа. Это могут быть длины дорог или плата за проезд, если граф моделирует карту какой-то местности. В таком случае граф называется взвешенным, а сами числа — весами. Пример: граф с шестью вершинами и семью рёбрами  Граф, в котором каждая пара вершин соединена ребром, называется полным. Обозначение: Kn – граф, состоящий из n вершин и ребер, соединяющих всевозможные пары этих вершин. Такой граф можно представить как n–угольник, в котором проведены все диагонали. Ниже приведены полные графы с числом вершин от 1 до 8 и количества их рёбер.
Степенью вершины называется число ребер, которым принадлежит вершина (число рёбер с концом в данной вершине). Дополнением данного графа называется граф, состоящий из всех ребер и их концов, которые необходимо добавить к исходному графу, чтобы получить полный граф. Граф, который можно представить на плоскости в таком виде, когда его ребра пересекаются только в вершинах, называется плоским. Многоугольник плоского графа, не содержащий внутри себя никаких вершин или ребер графа, называют его гранью. Понятия плоского графа и грани графа применяется при решении задач на «правильное» раскрашивание различных карт. Путем от вершины A до вершины X называется последовательность ребер, ведущая от A к X, такая, что каждые два соседних ребра имеют общую вершину, и никакое ребро не встречается более одного раза. Циклом называется путь, в котором совпадают начальная и конечная точка (т.е. можно «ходить по циклу» — «ходить по кругу»).  Простым циклом называется цикл, не проходящий ни через одну из вершин графа более одного раза. Длиной пути, проложенного на цикле, называется число ребер этого пути. Две вершины A и B в графе называются связными (несвязными), если в нем существует (не существует) путь, ведущий из A в B. Граф называется связным, если каждые две его вершины связны; если же в графе найдется хотя бы одна пара несвязных вершин, то граф называется несвязным. https://habr.com/ru/company/otus/blog/568026/ Специальным типом графов является дерево. В дереве выделяется особая вершина — корень, которая соединена рёбрами с другими вершинами — своими потомками, которые в свою очередь могут иметь своих потомков. Вершина, не имеющая потомков, называется листом. Наглядный пример дерева — иерархия файлов и папок в файловой системе компьютера или систематика живых организмов 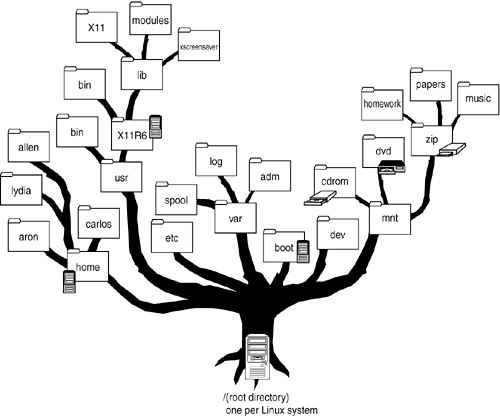 Если не выделять особым образом корень, то дерево — это просто любой связный граф, не имеющий циклов |