матемтике. Изоклины представляют собой гиперболы
 Скачать 58.45 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ МАТЕМАТИКА Группа Го20М661 Студент Курбонова С.У МОСКВА 2023 1. Методом изоклин построить интегральные кривые уравнения 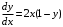 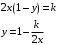 Если y=k ,то k=2x(1-y)  =1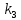 =2 =10Изоклины представляют собой гиперболы. 1. Строится достаточно густая сетка изоклин для различных значений k и на каждой изоклине изображаются небольшие отрезки с наклоном k. 2. Начиная из точки (x0, y0), поводится линия, которая, будет пересекать каждую изоклину под углом, заданным полем направлений. Полученная таким образом кривая и будет приближенным изображением (эскизом) интегральной кривой уравнения, проходящей через точку (x0, y0). 2. Решить уравнение, допускающее понижения порядка 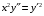 Делаем замену  . Тогда  . 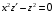Подставляя в исходное уравнение получаем: Это неоднородное уравнение. Сделаем замену переменных:   или 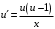 Преобразуем уравнение так, чтобы получить уравнение с разделяющимися переменными: 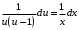 Интегрируя, получаем: 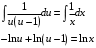 Учитывая, что z = ux, u=z/x получаем: 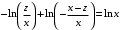 Поскольку y'=z, то интегрируя, окончательно получаем:  3. Решить систему уравнений 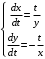 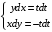   4. Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10? Решение Наивероятнейшее число k0 определяют из двойного неравенства 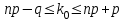 таким образом: 1) если число np – q дробное, то существует одно наивероятнейшее число k0; 2) если число np – q целое, то существует два наивероятнейших числа, а именно: k0 и k0 + 1; 3) если число np целое, то наивероятнейшее число k0 = np. пусть провел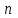и  испытаний.Имеем:      .Ответ: . |