Изучение законов динамики и кинематики поступательного движения на машине атвуда

• Название: Изучение законов динамики и кинематики поступательного движения на машине атвуда
• Дата: 24.10.2021
• Размер: 1.41 Mb.
• Имя файла: LR104.doc
• Тип: Лабораторная работа; #254950
• страница: 1 из 4

Лабораторная работа 104

ИЗУЧЕНИЕ ЗАКОНОВ ДИНАМИКИ И КИНЕМАТИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ НА МАШИНЕ АТВУДА
Теория

Механика - это наука о простейших формах движения и силах, вызывающих это движение.

Механическим движением называется изменение с течением времени взаимного положения тел или частей тела друг относительно друга.

Развитие механики как науки начинается с 3 в. до н. э., когда древнегреческий ученый Архимед сформулировал закон равновесия рычага и законы равновесия плавающих тел. Основные законы механики установлены итальянским физиком и астрономом Галилео Галилеем и окончательно сформулированы английским ученым Исааком Ньютоном.

Механика Галилея – Ньютона называется классической механикой. В ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме (3·10⁸ м/с).

Механика делится на три раздела: кинематику, динамику и статику.

Кинематика - это раздел физики, который изучает движение тел вне зависимости от причин, вызывающих это движение.

Динамика изучает законы движения тел и причины, которые вызывают или изменяют это движение.

Статика изучает законы равновесия системы тел. Если известны законы движения тел, то из них можно установить и законы равновесия. Поэтому законы статики отдельно от законов динамики физика не рассматривает.

Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Простейшей моделью является материальная точка. Под материальной точкой понимают любое тело, размерами и формой, которого можно пренебречь в данной задаче. Одно и тоже тело, в зависимости от постановки задачи может быть рассмотрено как материальное тело или материальная точка.

Произвольное макроскопическое тело или систему тел можно мысленно разбить на малые взаимодействующие между собой части, каждая из которых рассматривается как материальная точка. Тогда изучение движения произвольной системы тел сводится к изучению системы материальных точек. В механике сначала изучают движение одной материальной точки, а затем переходят к изучению движения системы материальных точек.

Под воздействием тел друг на друга тела могут деформироваться, то есть менять свою форму и размеры. Поэтому в механике вводится еще одна модель – абсолютно твердое тело. Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя точками (или точнее между двумя частицами) этого тела остается постоянным.

Различают три вида механического движения тел – поступательное, вращательное и колебательное.

Поступательное движение – это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Колебательным движением называется процесс, при котором система, многократно отклоняясь от своего состояния равновесия, каждый раз вновь возвращается к нему.

Поступательное движение характеризуется векторами: перемещения, скорости и ускорения.

Л 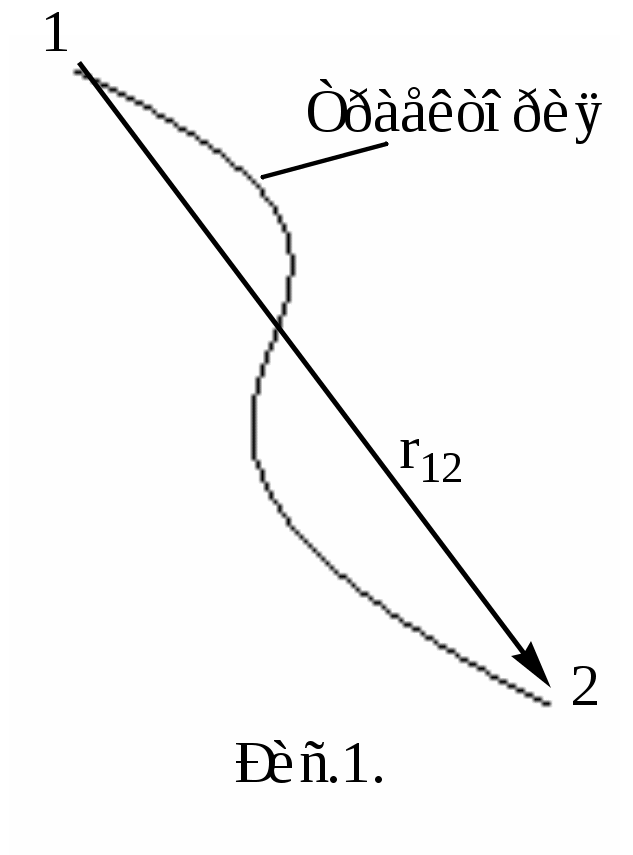иния, которую описывает материальная точка при движении, называют траекторией (рис. 1). Вне зависимости от формы траектории различают прямолинейное и криволинейное движение. Движение называется прямолинейным, если траектория прямая линия, и криволинейным, если траектория – кривая линия

П 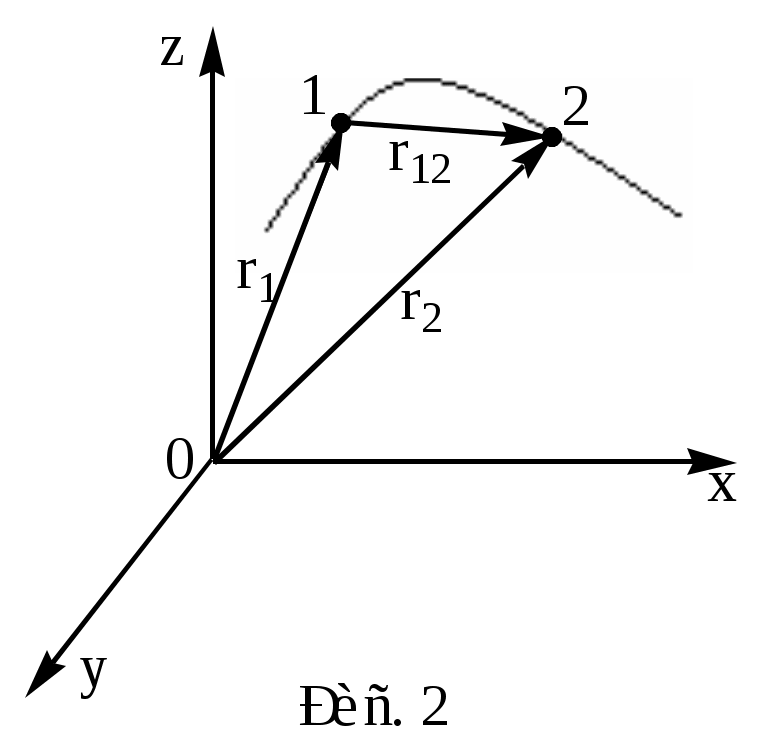еремещение– это вектор , направленный из начального положения материальной точки в ее конечное положение – приращение радиуса вектора точки за рассматриваемый промежуток времени

Путь – это длина траектории от начального положения материальной точки до конечного. Путь - величина скалярная.

Под элементарным вектором перемещения точки понимают приращение радиуса-вектора этой точки за промежуток времени .

Радиус-вектор – это вектор, проведенный из начала системы координат, в которой изучается движение, в данную точку.

Для характеристики движения материальной точки вводится векторная величина – скорость, которой определяется как быстрота движения, так и его направление в данный момент времени.

П 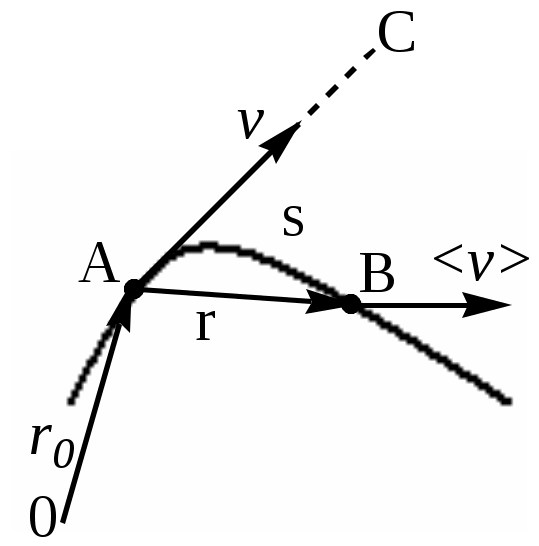усть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус вектор . В течение малого промежутка времени Δt точка пройдет малый путь Δs и получит элементарное (бесконечно малое) перемещение .

Отношение пути, пройденного материальной точкой, к промежутку времени, за который этот путь пройден, называется средней скоростью движения:

(1.3)

- скалярная величина.

Вектором средней скорости называется отношение приращения радиуса вектора точки к промежутку времени Δt

(1.4).

Направление вектора средней скорости совпадает с направлением .

В общем случае криволинейного (и прямолинейного) движения средняя скорость может быть различной на разных участках траектории и зависеть от пути Δs, или, что то же, от промежутка времени Δt. Следовательно, 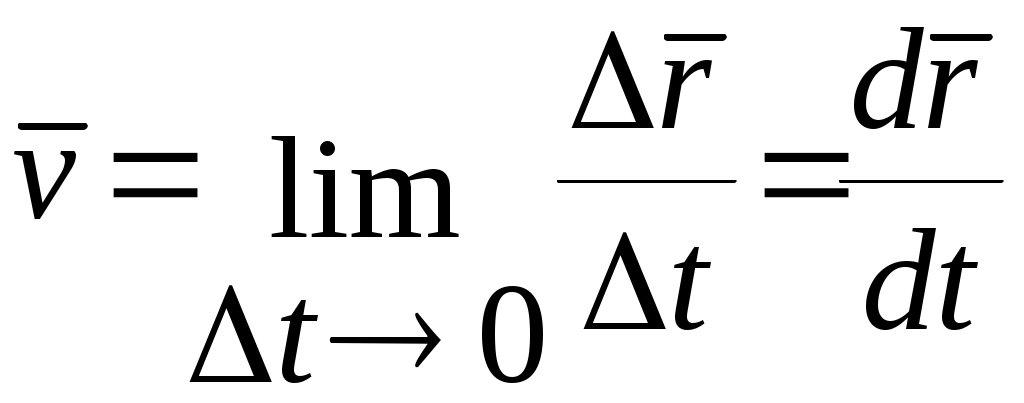недостаточно полно характеризует движение. Поэтому вводят понятия мгновенной скорости (скорости в данный момент времени в данной точке пути). Будем бесконечно уменьшать промежуток времени, то есть предположим Δt→0. Тогда точка В стремится к точке А, хорда АВ – к дуге Δs и обе они в пределе совпадут с касательной АС. Таким образом, криволинейное движение по малой дуге Δs перейдет в прямолинейное движение по бесконечно малому отрезку касательной к траектории вблизи точки А, а средняя скорость на малом пути Δs перейдет в мгновенную скорость в точке А, направленную по касательной к траектории. Таким образом, мгновенная скорость , есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени

(1.5).

При уменьшении Δt до предела Δs= модуль мгновенной скорости равен первой производной пути по времени

(1.6).

Из формул 1.5 и 1.6 следует, что скорость выражается в метрах в секунду.

Если направление вектора точки не изменяется, то траектория точки – прямая линия. В случае криволинейного движения точки направление ее скорости непрерывно изменяется. При равномерном движении точки остается постоянным модуль скорости v , в то время как направление вектора изменяется произвольным образом, а путь пройденный точкой за промежуток времени Δt равен

(1.7).

В этом случае точка проходит за равные промежутки времени один и тот же путь. Если точка движется равномерно и прямолинейно со скоростью вдоль оси ОХ, то зависимость ее координаты х от времени имеет вид:

(1.8),

где х₀ – значение х в начальный момент времени (t=0),

v_х – проекция скорости точки на ось ОХ.

Если модуль вектора скорости точки изменяется с течением времени, то такое движение точки называется неравномерным. Для характеристики быстроты изменения скорости т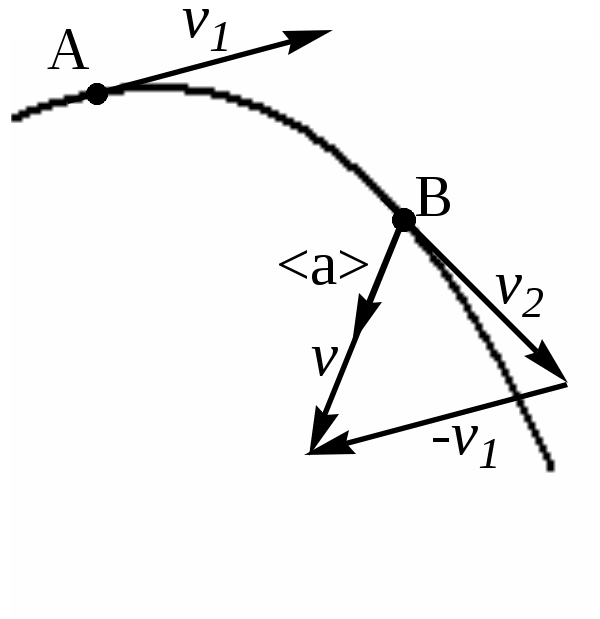очки в механике вводится векторная физическая величина, называемая ускорением.

П усть материальная точка переместилась за малый промежуток времени Δt из А, где она имела скорость , в В, где она имеет скорость . Изменение (приращение) скорости точки есть вектор , равный конечной и начальной скоростей:

(1.9).

Отношение изменения скорости к промежутку времени, за которое это изменение произошло, называется средним ускорением

(1.10).

Из правила деления вектора на скаляр следует, что среднее ускорение направлено так же, как приращение скорости, то есть под углом к траектории в сторону ее вогнутости.

В общем случае среднее ускорение может быть различным на различных участках траектории. Оно зависит от промежутка времени, по которому проводится усреднение. Будем уменьшать промежуток времени. В пределе при Δt→0 точка В будет стремиться к точке А и среднее ускорение на пути АВ превратиться в мгновенное ускорение в точке А

(1.11).

Таким образом, мгновенное ускорение движения в любой точке - это вектор, направленный под углом к траектории в сторону ее вогнутости, определяемый как первая производная вектора скорости по времени или степень изменения скорости во времени. Математически ускорение- это вторая производная радиус-вектора по времени.

Из формул 1.10 и 1.11 следует, что ускорение выражается в метрах на секунду в квадрате (м/с²).

В 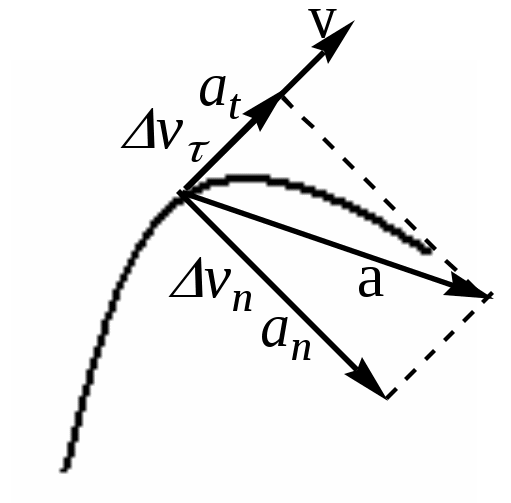ектор ускорения принято раскладывать на две составляющие, одна из которых направлена по касательной к траектории и называется касательным или тангенциальным ускорением , другая – по нормали к траектории и называется нормальным или центростремительным ускорением .

Тангенциальная составляющая ускорения равна первой производной по времени от модуля скорости, характеризует быстроту изменения скорости по модулю, направлена по касательной к траектории

(1.12).

Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению и направлена к центру кривизны траектории

(1.13).

Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющей

(1.14),

численно равна

(1.15).

В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:

1) = 0, =0 – прямолинейное равномерное движение.

2) = а = const, .=0 – прямолинейное равнопеременное движение (равноускоренное, если >0, и равнозамедленное, если <0). При таком виде движения

(1.16).

Если начальный момент времени t₁ = 0, а начальная скорость v₁ = v₀, то обозначив t₂ = t и v₂ = v, получим a=(v-v₀)/t, откуда

(1.17).

Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t, найдем, что длина пути, пройденного точкой, в случае равнопеременного движения

(1.18).

3) = f(t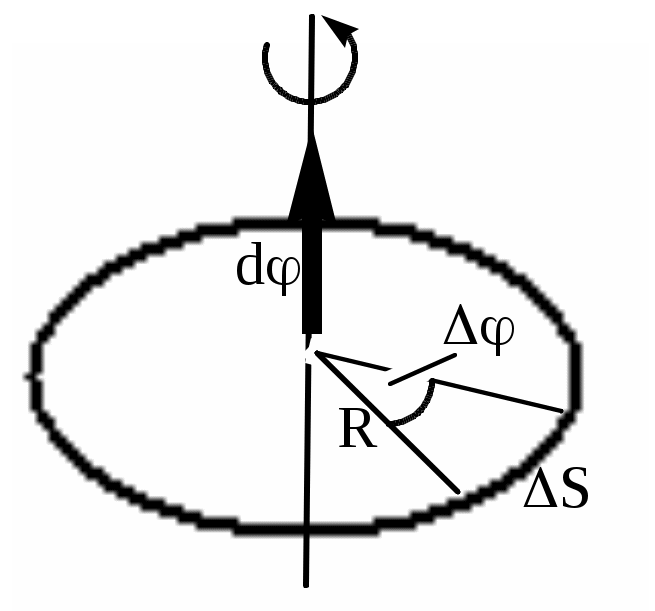), .=0 – прямолинейное движение с переменным ускорением – ускоренное движение;

4) = 0, .= const. При = 0 скорость по модулю не изменяется, а изменяется по направлению. Из формулы 1.13 ( ) следует, что радиус кривизны должен быть постоянным. Следовательно, это есть равномерное движение по окружности;

5) = 0, .≠0 – равномерное криволинейное движение;

6) = const, . ≠0 – криволинейное равнопеременное движение;

7) = f(t), . ≠0 – криволинейное движение с переменным ускорением.

Р ассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдельные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R. Ее положение через промежуток времени Δt зададим углом Δφ. Элементарные (бесконечно малые) повороты можно рассматривать как векторы (они обозначаются или ). Модуль вектора равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, то есть подчиняется правилу правого винта («правило буравчика»). Векторы, направления которых связываются с направлением вращения, называются псевдовекторами или аксиальными векторами. 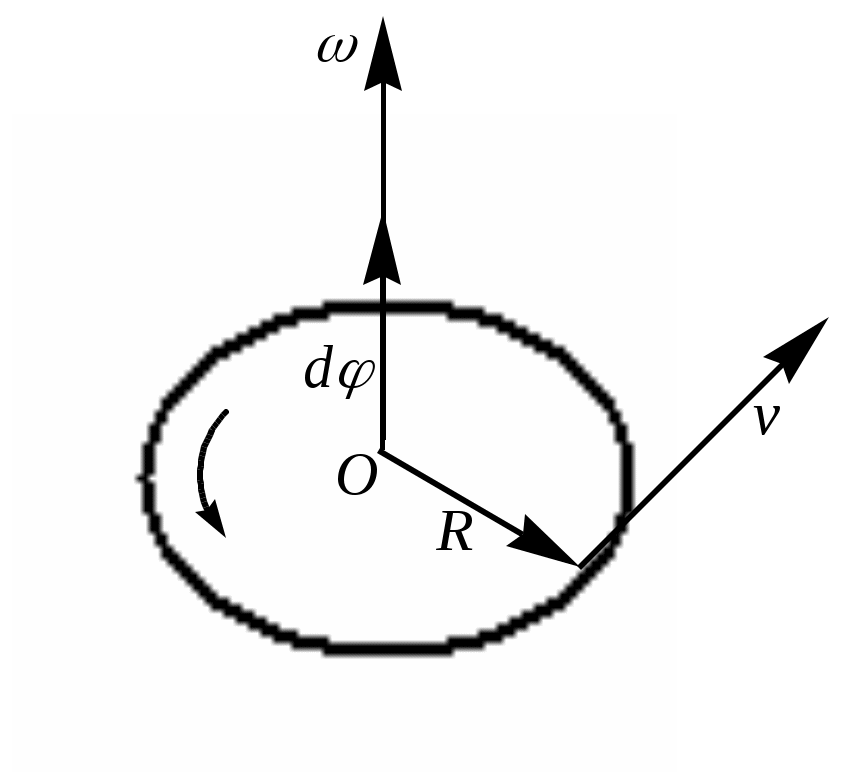Эти векторы не имеют определенных точек приложения: они м огут откладываться из любой точки оси вращения.

Отношение угла поворота к промежутку времени, за который этот поворот произошел называется угловой скоростью . Угловая скорость - векторная величина, равная первой производной угла поворота тела по времени:

(1.19).

Вектор направлен вдоль оси вращения по правилу правого винта, то есть так же, как и вектор . Единица измерения угловой скорости – радиан в секунду (рад/с).

Линейная скорость точки равна

(1.20), то есть

(1. 21).

В векторном виде формулу для линейной скорости можно написать как векторное произведение

(1.22).

При этом модуль векторного произведения, по определению, равен , а направление совпадает с направлением поступательного движения правого винта при его вращении от к .

Если = const, то вращение равномерное и его можно характеризовать периодом вращения Т – временем, за которое точка совершает один полный оборот, то есть поворачивается на угол 2π. Так как промежутку времени Δt=Т соответствует Δφ=2π, то ω= 2π/Т, откуда

Т= 2π/ ω

Единица измерения периода – секунда (с).

Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения n

n = 1/Т = ω/2π, откудаω = 2πn

Единица измерения частоты – Герц (Гц) или с^-1.

При неравномерном движении материальной точки по окружности вместе с линейной изменяется и угловая. Поэтому можно ввести понятие углового ускорения. Отношение изменения угловой скорости к промежутку времени, за который это изменение произошло, называется угловым ускорением . Угловое ускорение – это векторная величина, равная первой производной угловой скорости по времени:

(1.24)

Единица измерения углового ускорения – радиан на секунду в квадрате (рад/с²).

П ри вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор сонаправлен вектору , при замедленном – противонаправлен ему.

Тангенциальная составляющая ускорения (1.25), подставляя (1.21) получим 1.26

Нормальная составляющая ускорения

1.27

Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение , нормальное ускорение ) и угловыми величинами (угол поворота φ, угловая скорость , угловое ускорение ) выражается следующими формулами:

; ; ; 1.28

В случае равнопеременного движения точки по окружности ( = const)

; 1.29,

где ω₀ – начальная угловая скорость