Лекция_6. Жидкости и газа
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
VI. УСТАНОВИВШАЯСЯ ФИЛЬТРАЦИЯ ОДНОРОДНОЙ СЖИМАЕМОЙ (УПРУГОЙ) ЖИДКОСТИ И ГАЗА Дифференциальные уравнения установившейся фильтрации упругой жидкости и газа по закону Дарси Составим дифференциальное уравнение фильтрации однородного сжимаемого флюида в однородной пористой среде на основе уравнения неразрывности потока (2.11) и уравнений движения (2.4) т.е. считаем фильтрацию сжимаемого флюида =(Р) по закону Дарси, процесс изотермический (Т=const), при этом вязкость флюида и проницаемость зависят от давления , т.е. =(Р) и k=k(Р). Введем обобщенную функцию давления тогда будем называть обобщенной функцией Лейбензона. Так как функция Из сравнения коэффициентов при dx, dy, dz, dt получаем Запишем выражения для массовых скоростей фильтрации с использованием (6.5) Далее, подставив (6.6) в уравнение неразрывности (6.1). получимили это и есть дифференциальное уравнение неустановившегося движения однородного флюида в однородной пористой среде по закону Дарси. В случае установившейся фильтрации или т.е. при установившейся фильтрации обобщенная функция Лейбензона Аналогия установившейся фильтрации сжимаемого флюида с фильтрацией несжимаемой жидкости Введение функции Лейбензона в уравнения позволяет установить аналогию между установившейся фильтрацией сжимаемого флюида и установившейся фильтрацией несжимаемой жидкости. В дальнейшем принимаем, что проницаемость среды и динамический коэффициент вязкости флюида постоянны, т.е. k=const и =const, а плотность флюида =(Р). Тогда можно ввести функцию Лейбензона как при этом Запишем закон Дарси для установившейся фильтрации несжимаемой жидкости в дифференциальной форме (1.15) через расход где Q=const; (S) - площадь поперечного сечения струйки. При установившейся фильтрации сжимаемого флюида по всей длине струйки массовый расход сохраняется постоянным: Qm= Q = const. Умножив обе части равенства (6.13) на плотность флюида (Р) и используя соотношение (6.12), имеем Легко видеть, что выражения (6.13) и (6.14) являются однотипными дифференциальными уравнениями, в которых объемному расходу Q несжимаемой жидкости соответствует массовый расход Qm сжимаемого флюида, а давлению в уравнении (6.13) соответствует функция Лейбензона Уравнения движения (6.2) для несжимаемой жидкости связывают скорость фильтрации V с давлением Р, а для сжимаемого флюида – массовую скорость фильтрации Отсюда вывод (аналогия): все формулы, полученные для установившейся фильтрации несжимаемой жидкости по закону Дарси, можно использовать и для установившейся фильтрации сжимаемого флюида в пластах той же геометрии и при тех же граничных условиях, заменив соответствующие параметры:
При этом помним, что при фильтрации сжимаемого флюида под давлением Р понимается абсолютное давление. Установившаяся фильтрация упругой жидкости Прежде всего найдем выражение функции Лейбензона для упругой (слабо сжимаемой) жидкости, описываемой уравнением состояния (2.14): Если 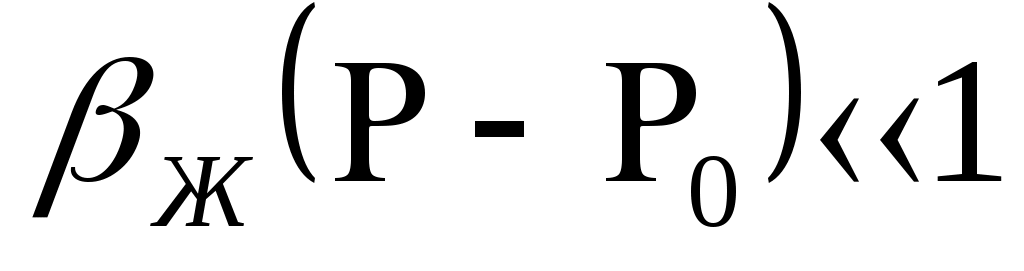 , то можно взять уравнения состояния упругой жидкости в виде (2.15). Тогда из (6.15) получаем следующее выражение для функции Лейбензона , то можно взять уравнения состояния упругой жидкости в виде (2.15). Тогда из (6.15) получаем следующее выражение для функции ЛейбензонаПодставив (6.16) в дифференциальное уравнение (6.9), получим Как следует из выражения (6.17), при установившейся фильтрации упругой жидкости плотность можно считать постоянной, поэтому при решении практических задач с установившейся фильтрацией упругой жидкости можно пользоваться формулами для установившейся фильтрации несжимаемой жидкости. Однако в случае фильтрации упругой жидкости в пласте с очень высоким пластовым давлением и при большой депрессии, следует использовать функцию Лейбензона (6.15), поскольку возможны большие погрешности. Прямолинейно-параллельный фильтрационный поток идеального газа На основании уравнения состояния идеального газа (2.18) при изотермическом процессе, находим функцию Лейбензона Используя аналогию между течением несжимаемой жидкости и течением газа найдем характеристики фильтрационного потока газа по аналогии с соответствующими характеристиками потока несжимаемой жидкости. Распределение давления в прямолинейно-параллельном фильтрационном потоке (рис.8) несжимаемой жидкости При фильтрации газа аналогичное соотношение справедливо для функции Лейбензона: Используя выражение функции Лейбензона (6.18) находим распределение давления Р(х) в прямолинейно-параллельном потоке идеального газа 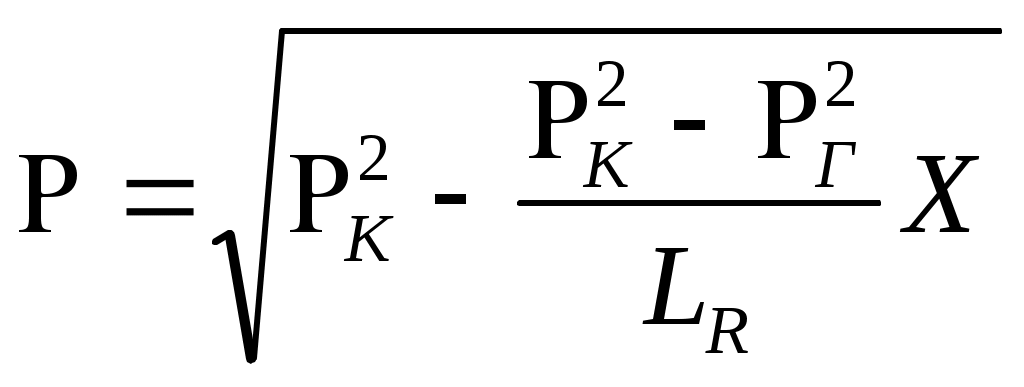 , (6.19) , (6.19)т 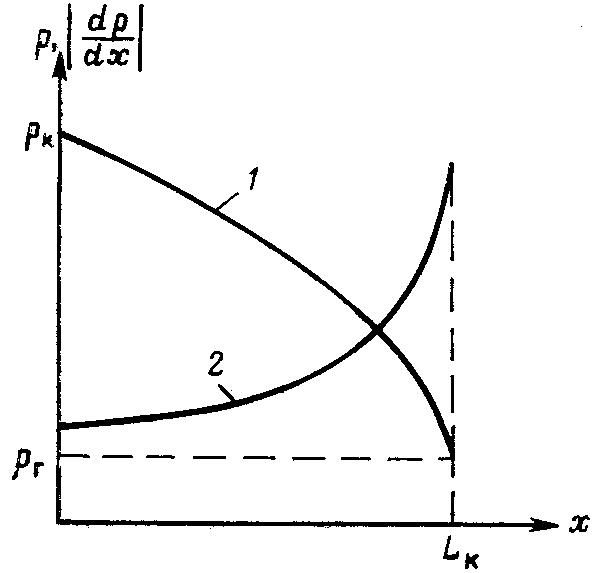 .е. давление по длине пласта Р(х) изменяется по параболическому закону (рис.36, кривая 1), а зависимость Р2(х) – прямолинейная. Рис. 36 Градиент давления в потоке несжимаемой жидкости имеет вид По аналогии градиент функции Лейбензона для потока газа будет Дифференцируя по Х выражение (6.18) и используя выражения 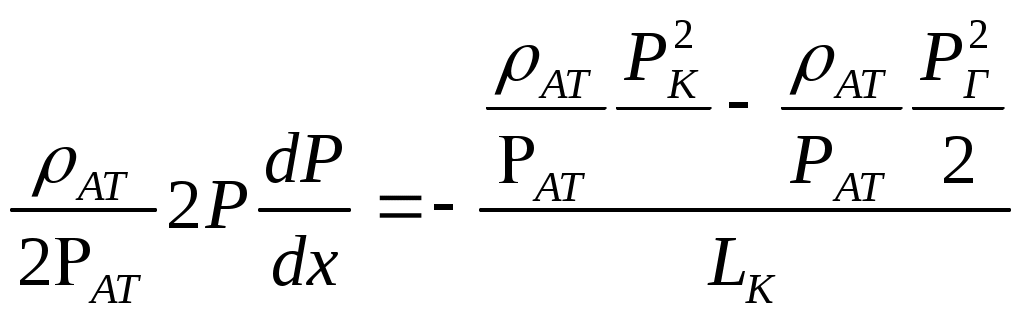 , ,откуда 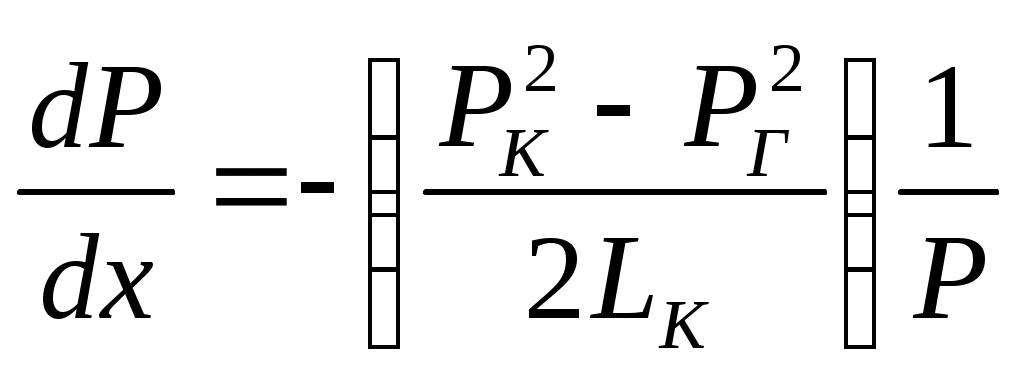 , ,где Р – определяется по формуле (6.19). График распределения градиента давления в потоке газа представлен на рис. 36, кривая 2. Градиент давления возрастает при приближении к галереи. 3) Объемный расход несжимаемой жидкости в рассматриваемом одномерном потоке Заменяя объемный расход Q массовым расходом Qm и давление Р функцией Лейбензона 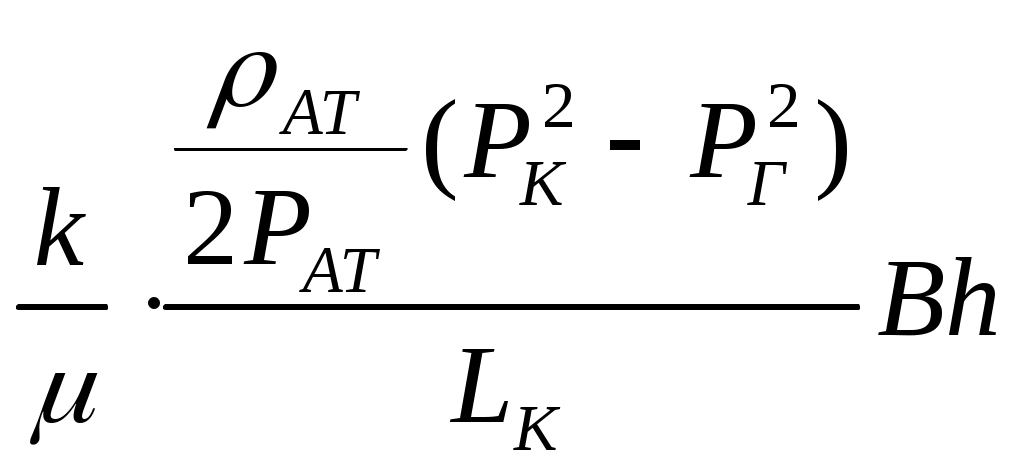 . (6.22) . (6.22)Тогда объемный расход газа, приведенный к атмосферному давлению, выражается формулой при фильтрации газа аналогично определяется массовая скорость фильтрации , т.е. откуда График функции V(x) аналогичен графику Средневзвешенное по объему порового пространства, занятого газом, пластовое давление В нашем случае Тогда 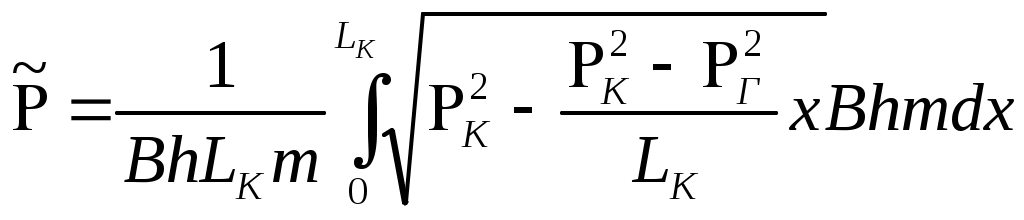 . .После интегрирования получим 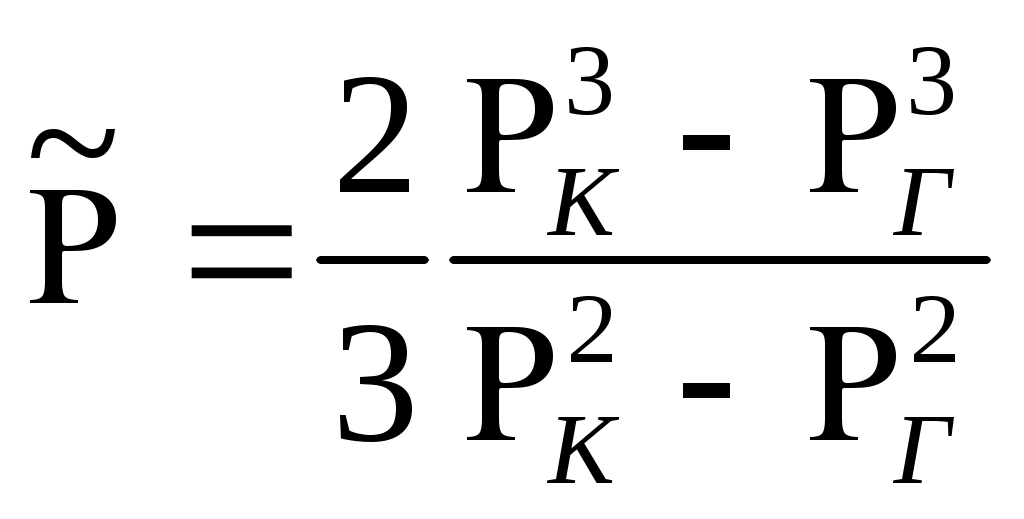 . (6.25) . (6.25)Плоскорадиальный фильтрационный поток идеального газа по закону Дарси Плоскорадиальный поток имеет место в круговом пласте радиусом RK , в центре которого имеется совершенная скважина радиусом re (Рис.9). Характеристику такого потока найдем, зная характеристики подобного потока несжимаемой жидкости. Распределение давления в потоке несжимаемой жидкости определяется по формуле 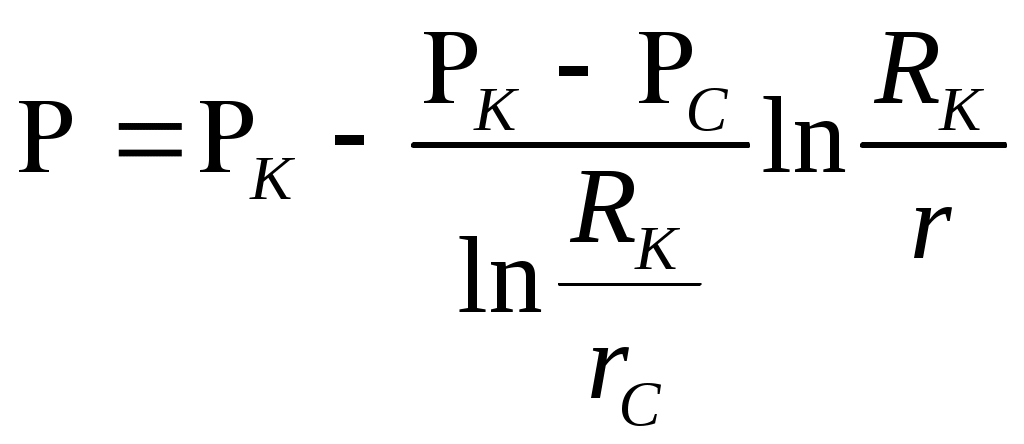 . (3.24) . (3.24)По этому же закону будет распределяться в фильтрационном потоке газа функция Лейбензона 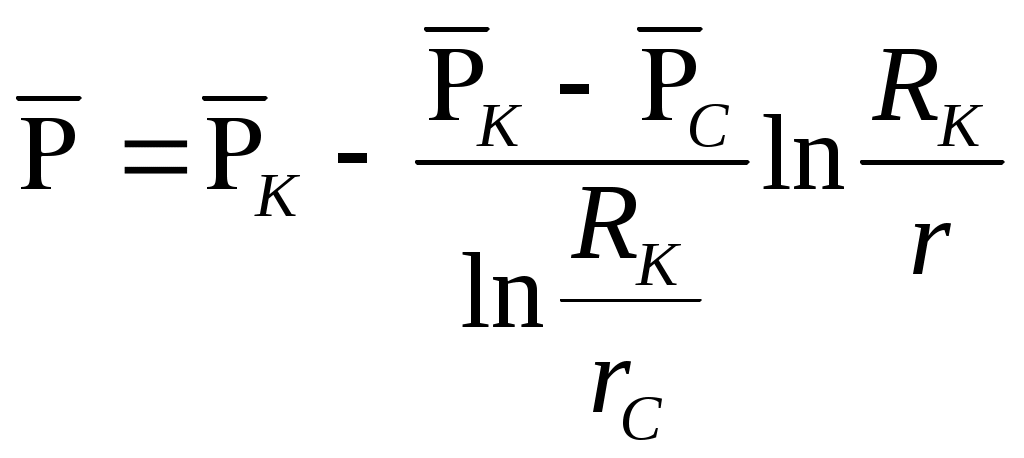 . (3.24) * . (3.24) *Подставив в (3.24)* выражение (6.18) для функции Лейбензона, получим закон распределения давления Р(r) в потоке идеального газа 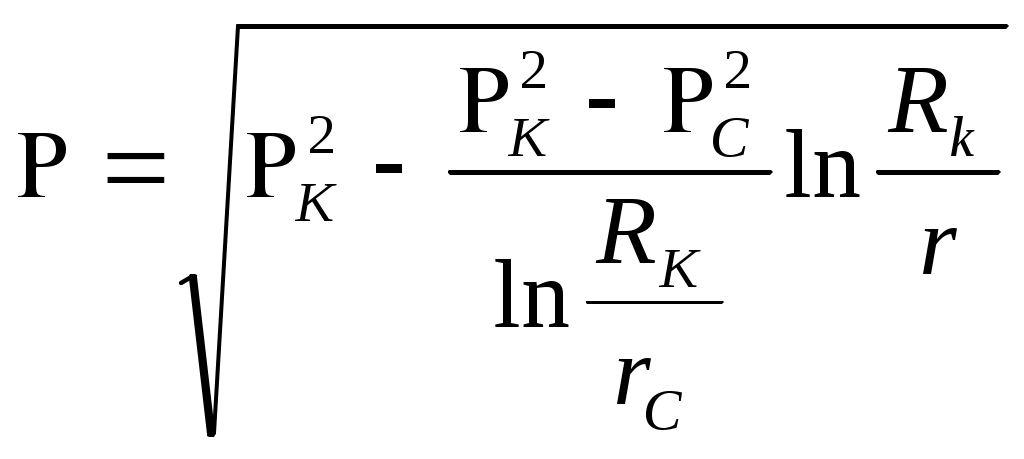 . (6.26) . (6.26)С 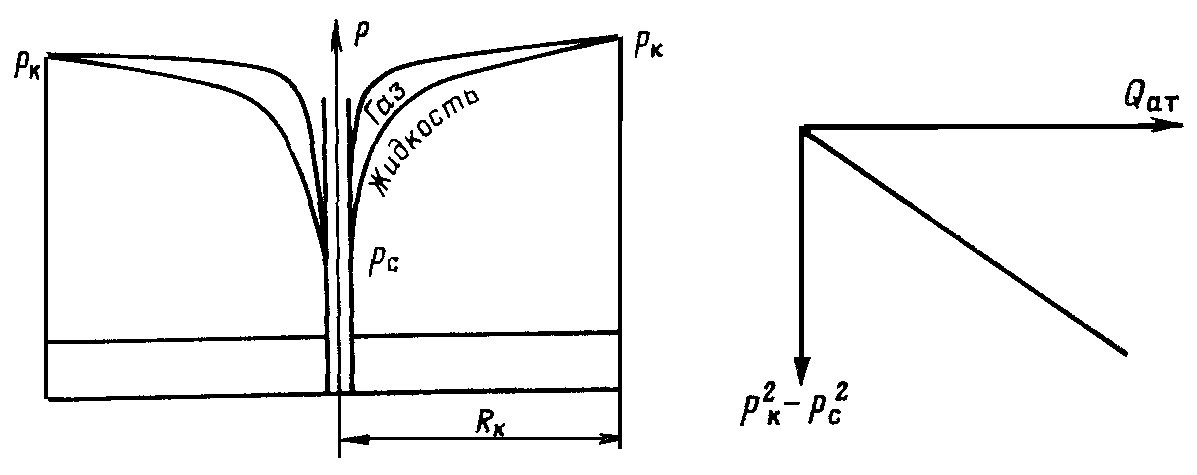 равнение кривых Р(r) для несжимаемой жидкости и идеального газа показывает (при одинаковых граничных условиях), что в газовом потоке имеет место резкое падение давления вблизи забоя скважины и весьма малое вдали от нее (рис. 37). Рис. 37 Рис. 38 Изменение градиента давления при плоскорадиальной фильтрации несжимаемой жидкости определяется формулой 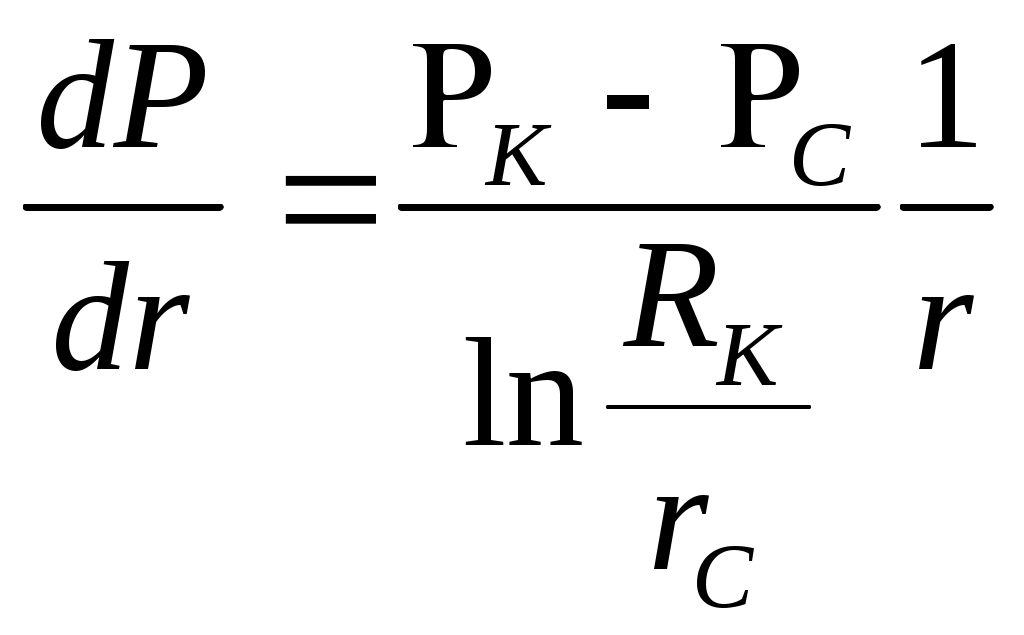 . (3.25) . (3.25)В случае установившейся фильтрации газа по такому же закону будет изменяться функция Лейбензона: 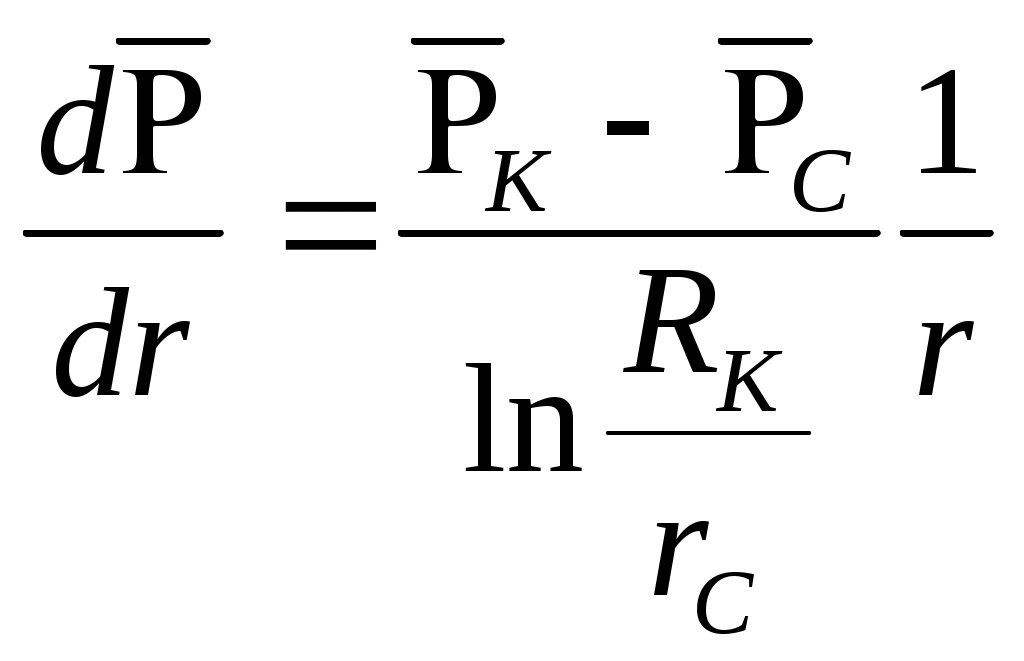 . (3.25)* . (3.25)*Переходя от функции Лейбензона (6.18) к давлению, получим 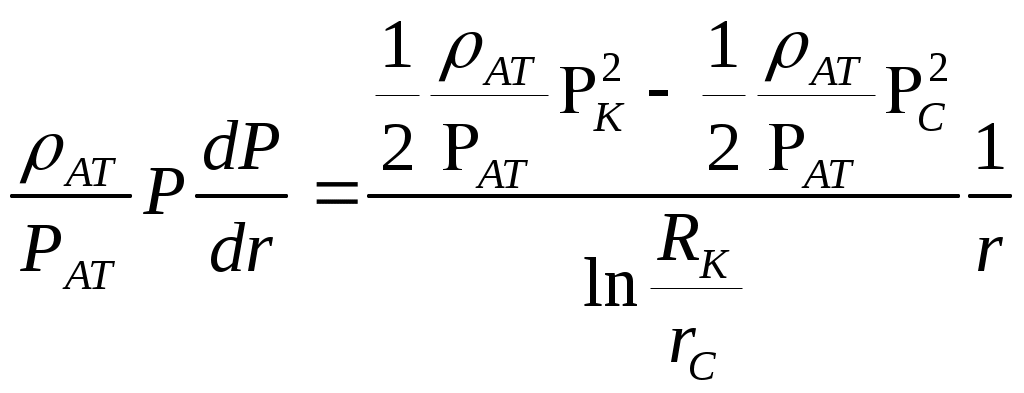 , ,откуда 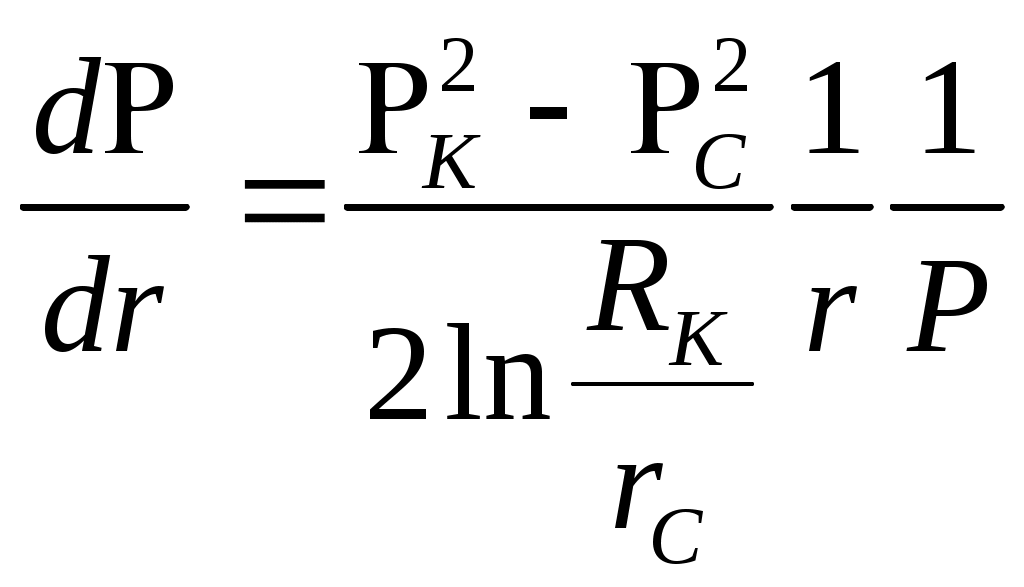 . (6.27) . (6.27)Из (6.27) следует, что градиент давления вблизи забоя скважины резко возрастает как за счет уменьшения r, так и за счет падения давления Р. Дебит газовой скважины получим, подставив в формулу Дюпюи (3.27) вместо объемного расхода Q сжимаемой жидкости массовый расход Qm газа и вместо давления Р функцию Лейбензона 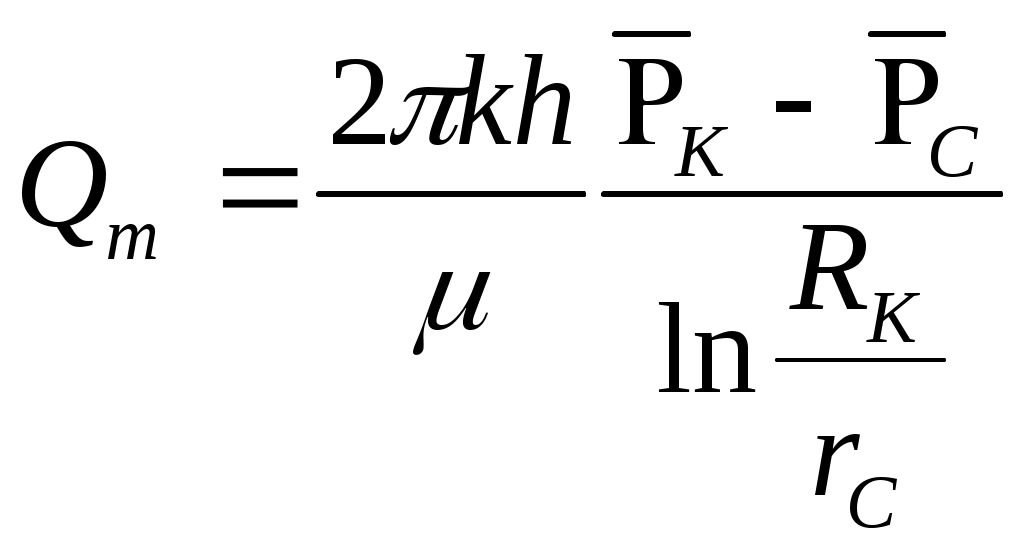 , (3.27)* , (3.27)*или 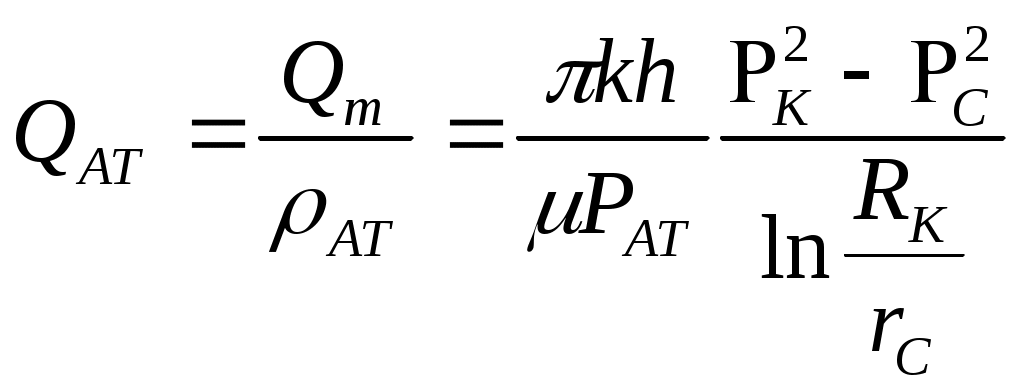 . (6.28) . (6.28)Индикаторная диаграмма при фильтрации газа строится в координатах QАТ и Если представить тогда выражение для дебита газа (6.28) можно представить так: 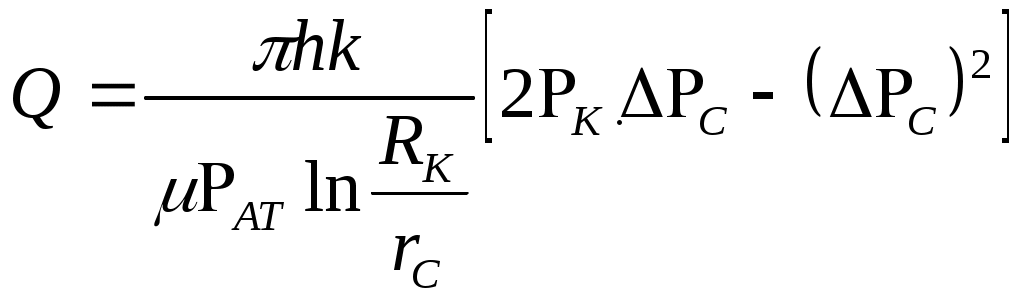 . (6.28)* . (6.28)*Уравнение (6.28)* в координатах Q и 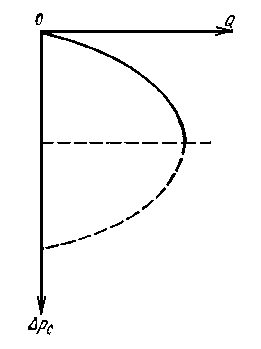 Рис. 39 Скорость фильтрации несжимаемой жидкости определяется по формуле 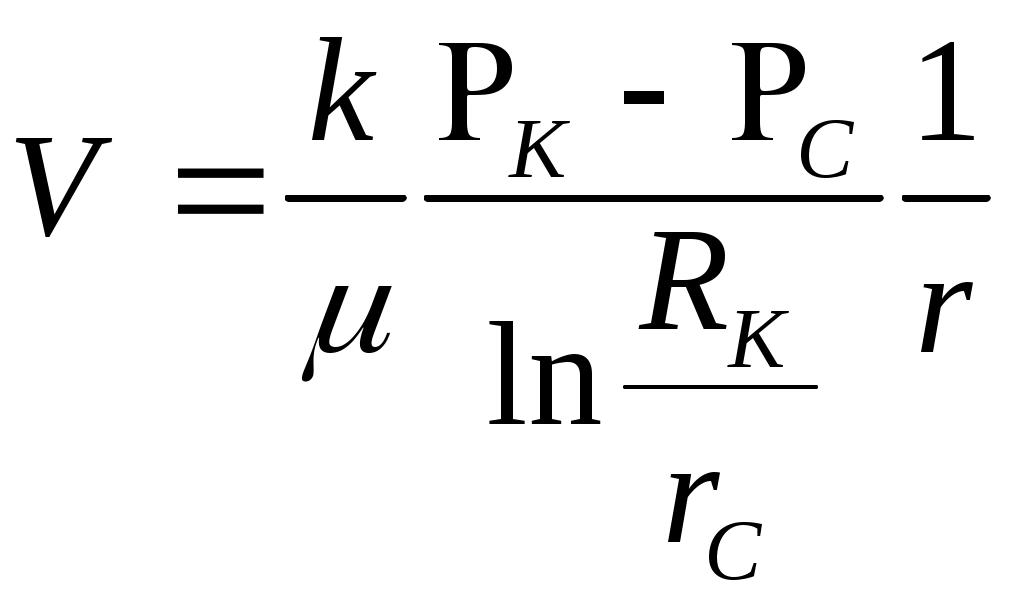 . (3.26) . (3.26)В плоскорадиальном потоке газа так же будет изменяться массовая скорость фильтрации 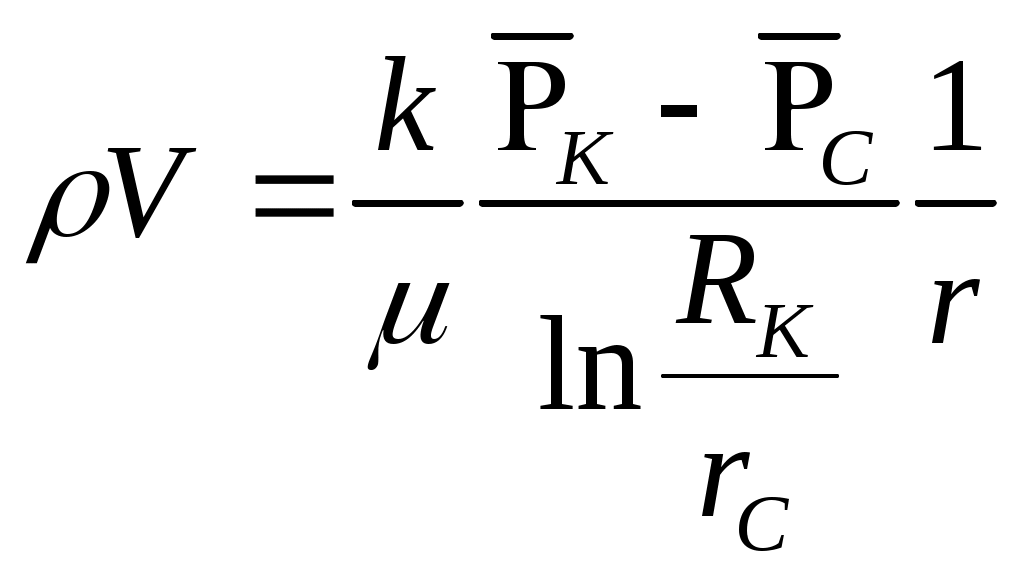 , (3.26)* , (3.26)*или 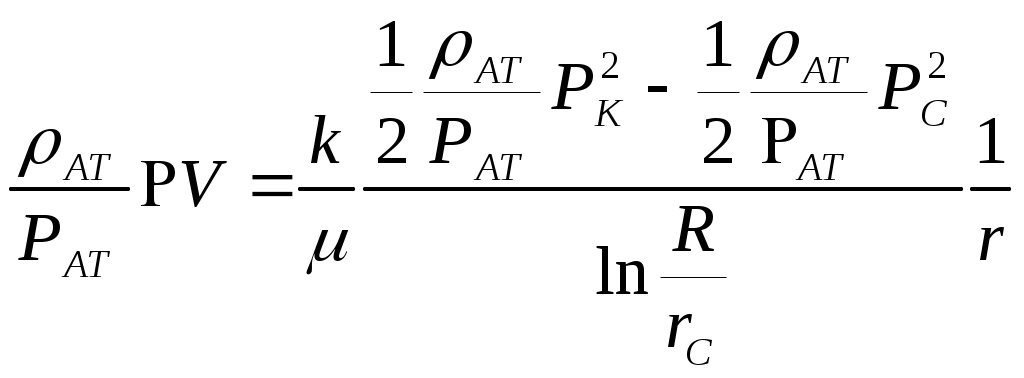 , ,откуда 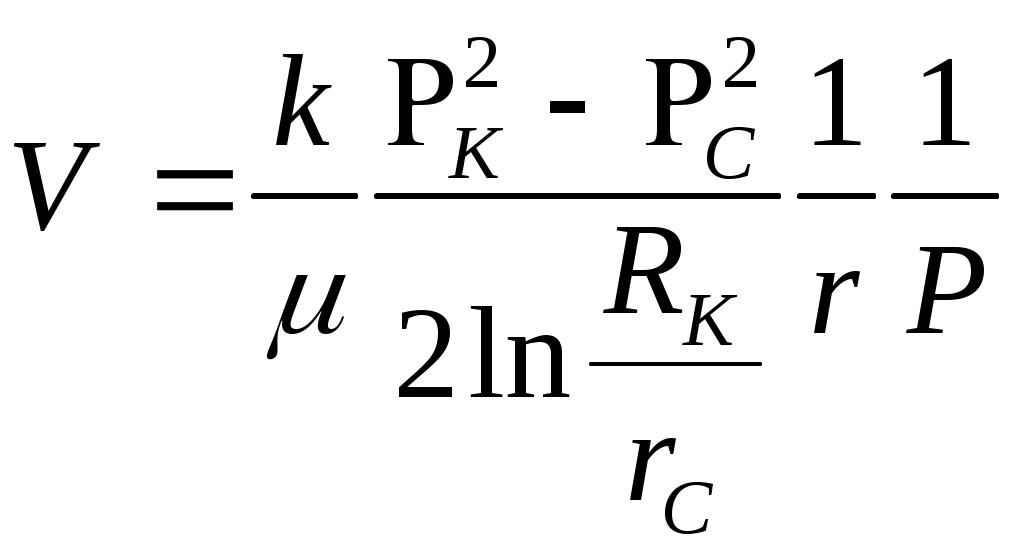 . (6.29) . (6.29) Определим средневзвешенное пластовое давление В нашем случае 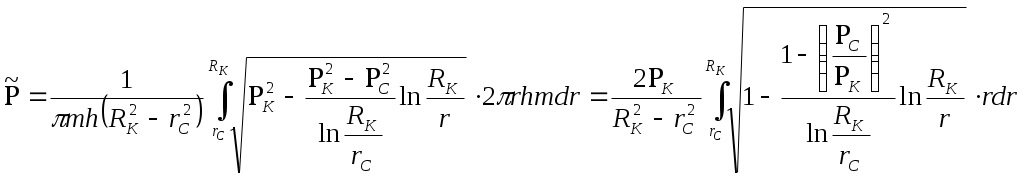 Полученный интеграл не берется в конечном виде и вычисляется приближенно. Получаем приближенное выражение для 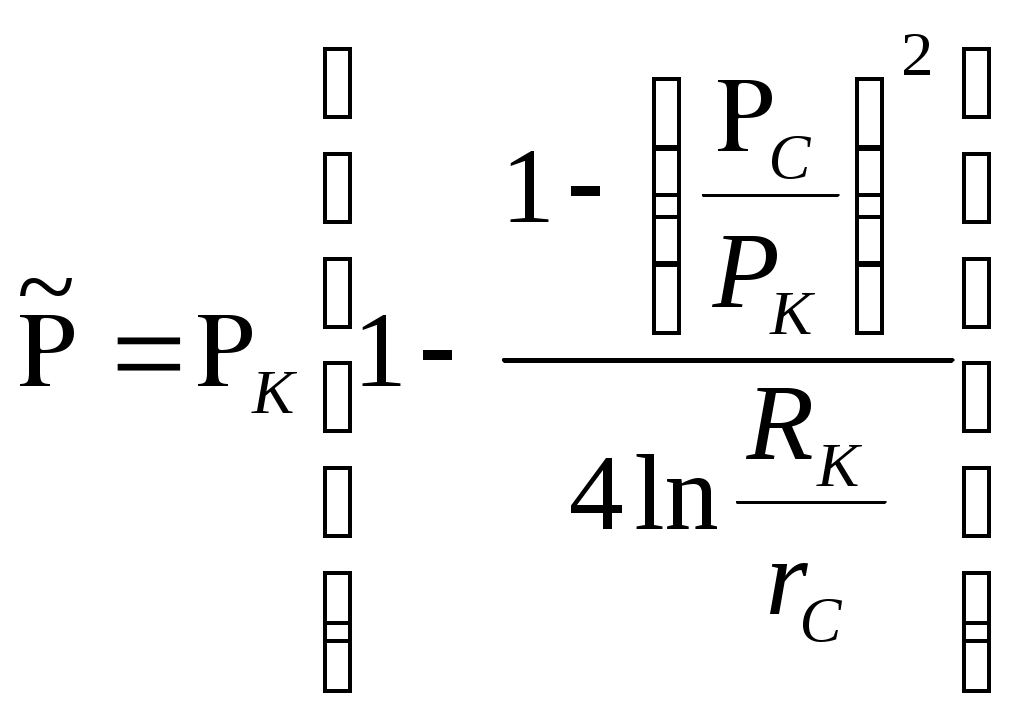 . (6.30) . (6.30)Расчеты по формуле (6.30) показывают, что Плоскорадиальный поток идеального газа по двучленному закону фильтрации Вблизи высокодебитных газовых скважин происходит нарушение закона Дарси, поэтому все гидродинамические расчеты строятся на основе двучленного закона фильтрации (5.10). При этом нельзя использовать диф. уравнение (6.9), т.к. оно получено с учетом уравнений движения по закону Дарси (6.2). Поэтому будем интегрировать уравнение (5.10), считая фильтрацию плоскорадиальной: т.е. Найдем распределение давления Р(r) в круговом пласте и выведем формулу притока газа к скважине. Выразим скорость фильтрации через приведенный объемный дебит 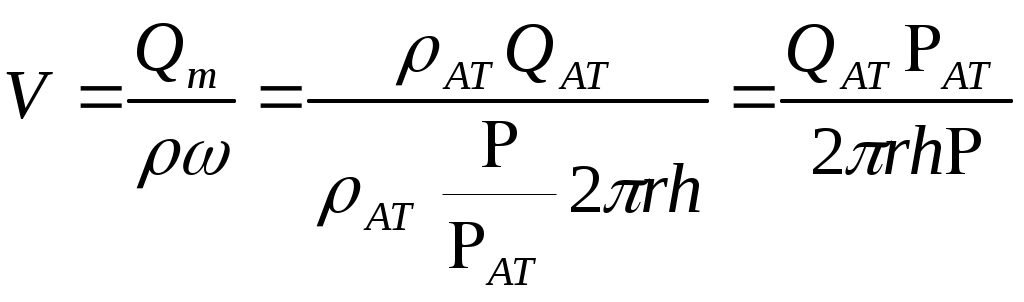 . (6.31) . (6.31)Подставим выражение (6.31) в (5.10) с учетом выражения (2.14) для (Р), получаем: Разделим переменные и проинтегрируем от забоя скважины (P=Pc; r=rc) до произвольной точки пласта (P;r): 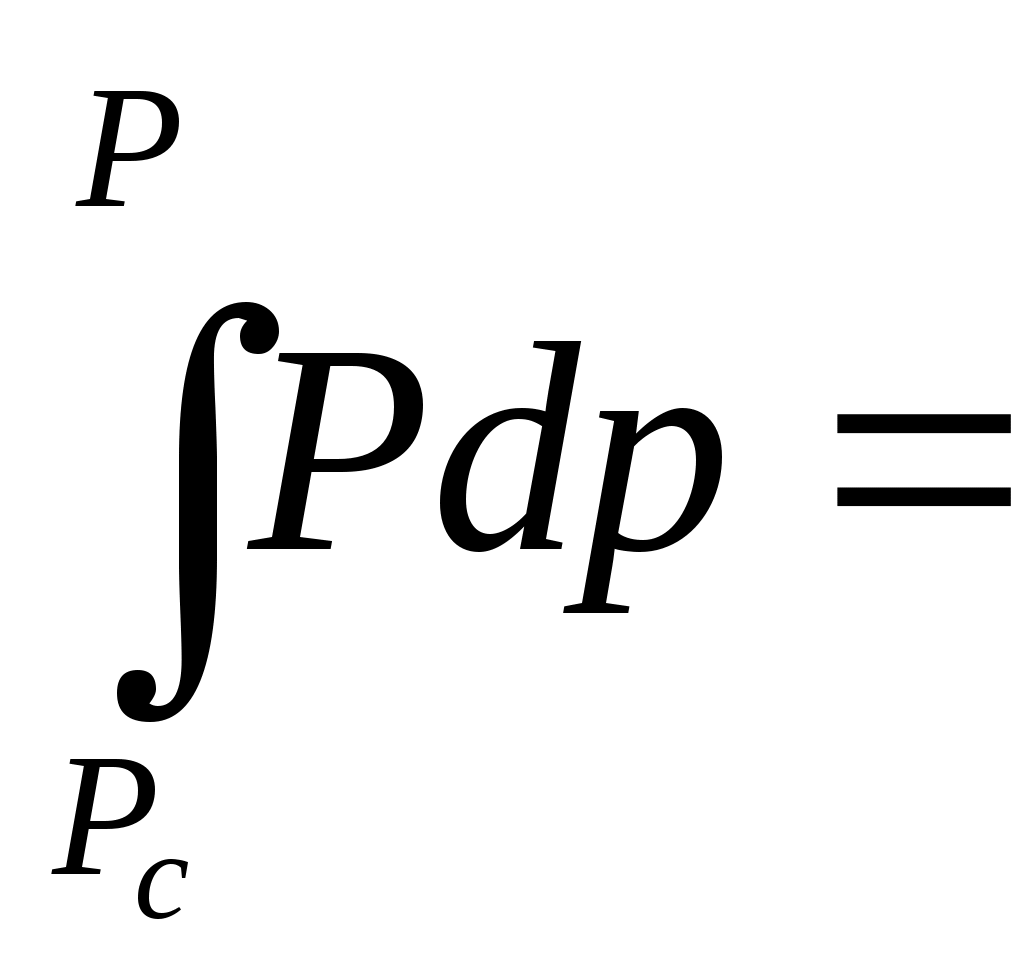 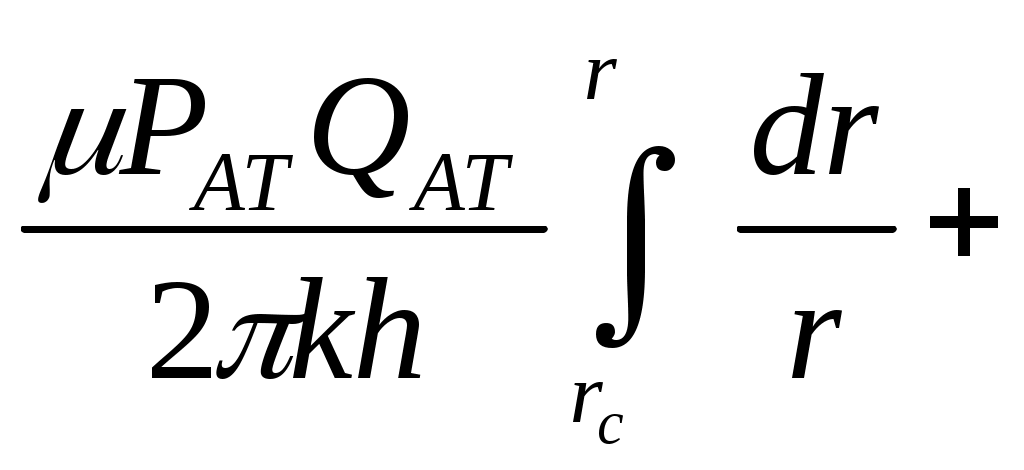 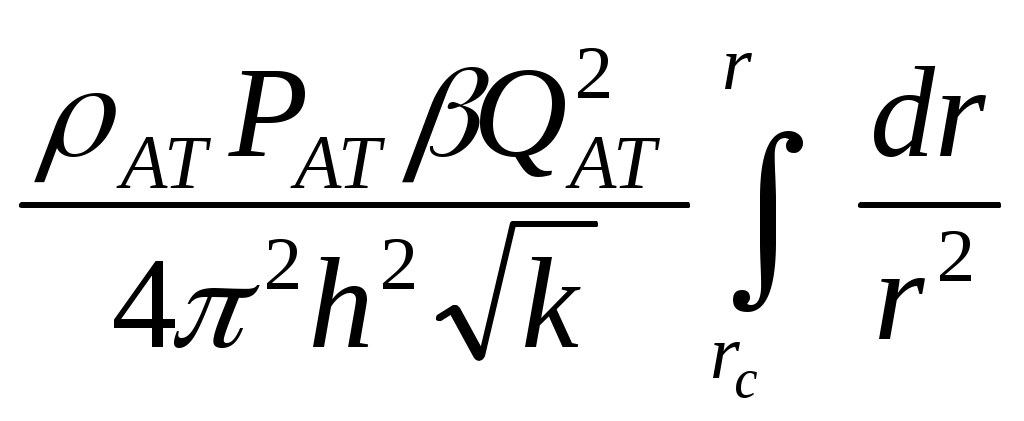 . .В результате будем иметь или 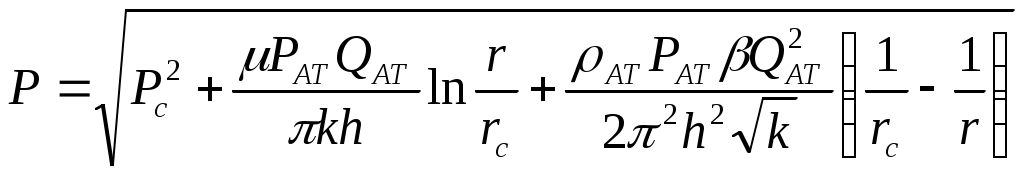 . (6.33) . (6.33)Распределение давления по формуле (6.33) отличается от распределения давления по формуле (6.26) ( при сохранении закона Дарси) наличием последнего слагаемого. Проинтегрируем уравнение (*) от забоя (P=Pc; r=rc) до контура питания (P=Pk; r=rk) и пренебрегая 1/Rk по сравнению с 1/rc , получим уравнение притока газа к скважине. 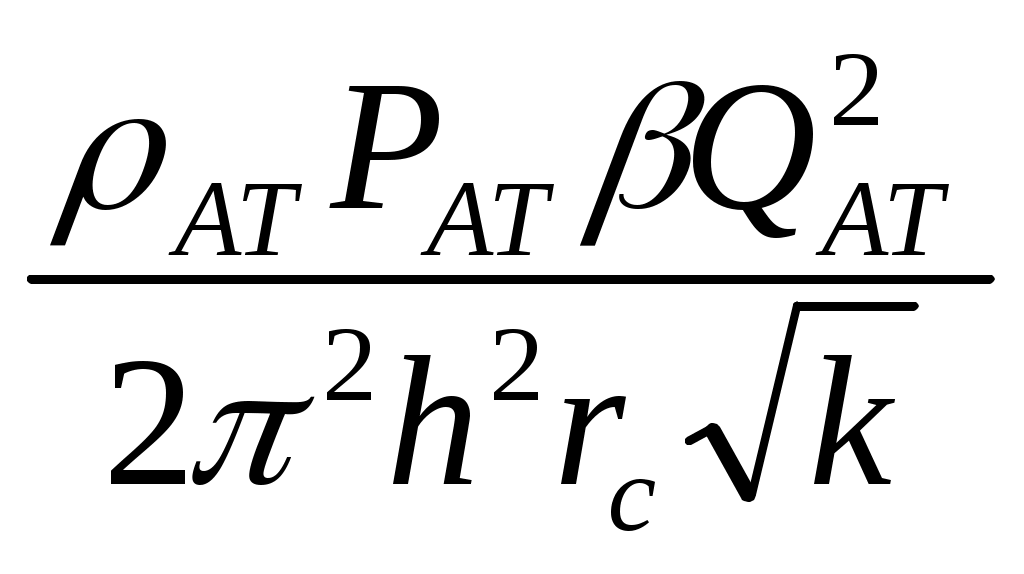 (6.34) (6.34)Обычно вводят обозначения: тогда уравнение (6.34) принимает вид: Коэффициенты фильтрационных сопротивлений А и B определяют опытным путем по данным исследования скважин при установившихся режимах. Газовая скважина исследуется на 5-6 режимах; на каждом режиме измеряется дебит и определяется забойное давление (по устьевому давлению). Затем скважину закрывают и давление в остановленной скважине принимают за контурное давление Pk. После этого можно найти (вычислить) значение коэф. А и В по индикаторной линии, построенной по уравнению (6.36) , которая представляет собой параболу выпуклостью к оси дебитов (рис.40). Однако удобнее уравнение (6.36) записать в виде : График уравнения (6.37) , построенный в координатах QАТ и 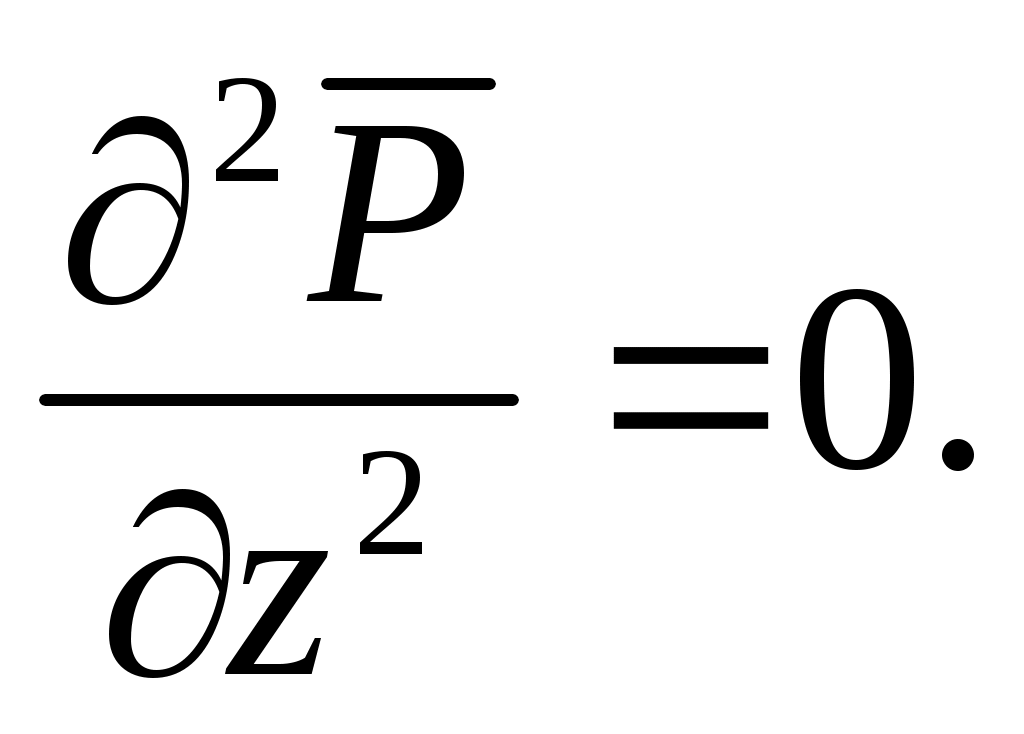 Рис. 40 Рис. 41 Уравнение притока (6.36) газа к скважине широко используется в расчетах при проектировании разработки газовых месторождений. Кроме того, по найденному значению А (путем исследования скважины) можно определить коллекторские свойства пласта, например, коэффициент гидропроводности 7. Плоскорадиальный фильтрационный поток реального газа по закону Дарси Если пластовое давление выше 10Мпа и депрессия не слишком мала (P/Pk т.е. Кроме того, для высоких пластовых давлений нужно учитывать зависимость вязкости от давления, которая определяется выражениями (2.21) или (2.22) или по графикам Если фильтрация установившаяся и выполняется закон Дарси, то справедливо уравнение (6.9) , в котором под функцией Лейбензона надо понимать выражение (6.4) , т.е. Для реального газа выражение (6.4) с учетом (2.16) имеет вид: Найдем дебит скважины при плоскорадиальном движении. Используя аналогично методу установившейся фильтрации несжимаемой жидкости и газа, напишем выражение для дебита , заменяя в ф-ле Дюпюи объемный дебит массовым, а KP/ 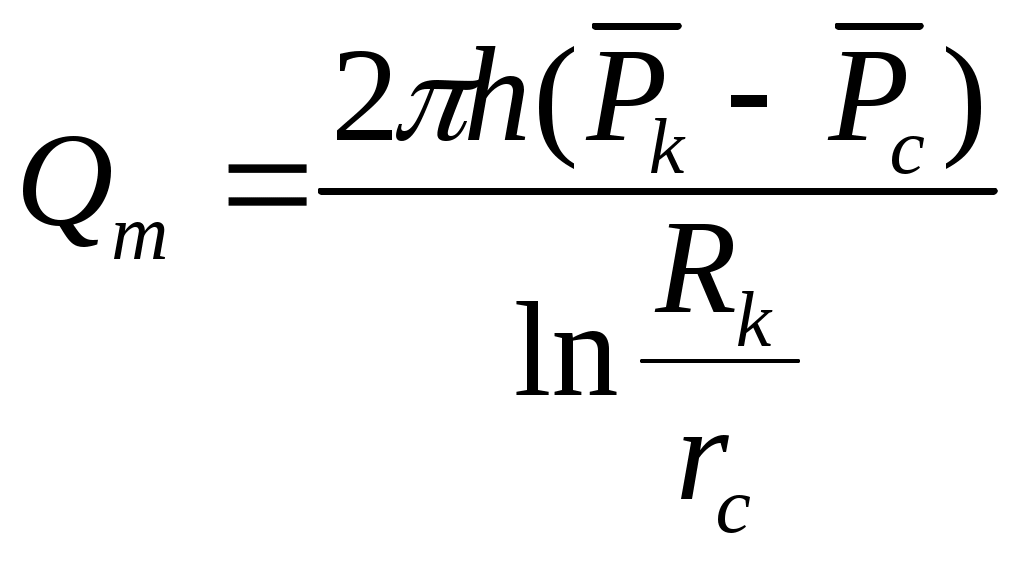 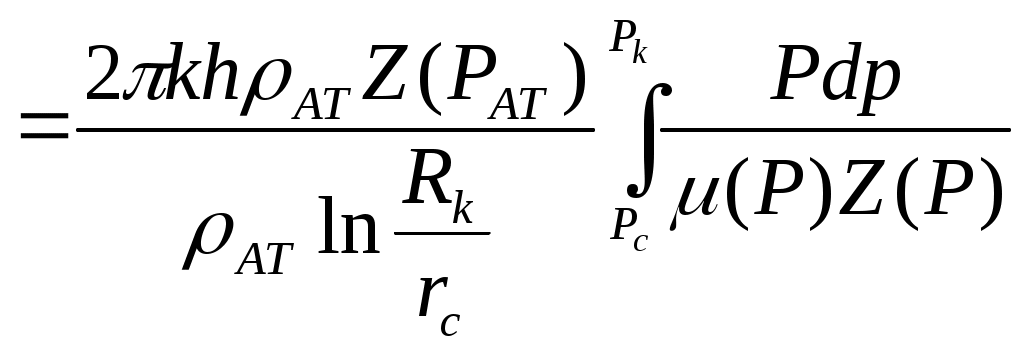 (6.40) (6.40)Переходим к дебиту , приведенному к атмосферному давлению 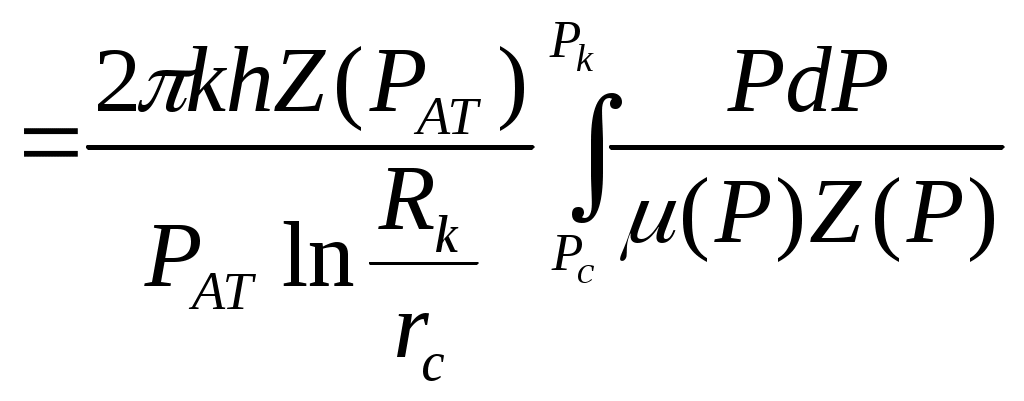 . (6.41) . (6.41)Вычисление интеграла в (6.41) можно произвести приближенно: по графикам зависимости Z(P) и (P) определяются значения Z(Pc)=Zc; Z(Pk)=Zk и Тогда интеграл в (6.41) вычисляется аналитически и формула (6.41) принимает вид  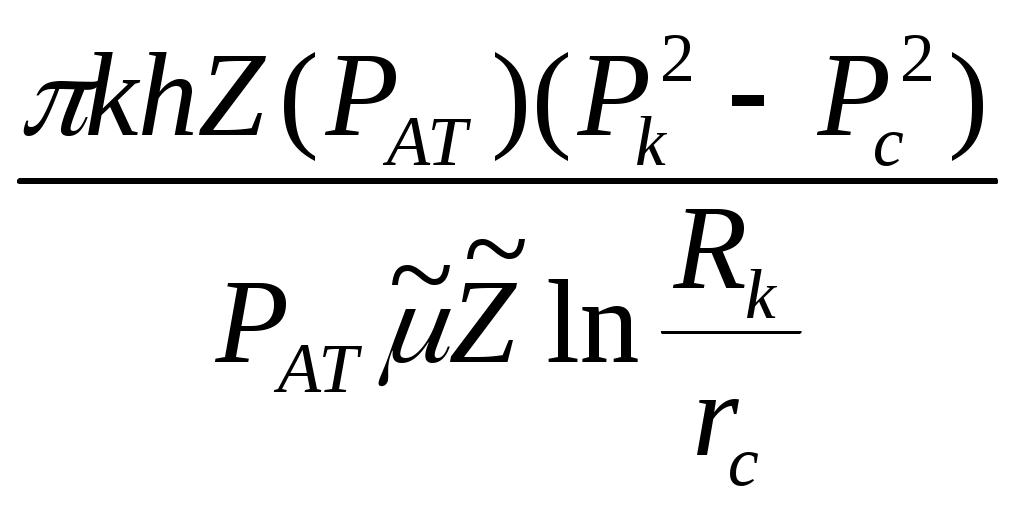 . (6.42) . (6.42)Как видим выражение (6.42) определяющее дебит реального газа отличается от выражения (6.28) для дебита идеального газа множителем |
