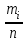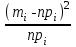Метрология. Кафедра арэо контрольная работа по дисциплине метрология, стандартизация и сертификация. Тема контрольного задания Обработка опытных данных по результатам многократных измерений
 Скачать 143.5 Kb. Скачать 143.5 Kb.
|
|
Федеральное Агентство Воздушного Транспорта Федерального Государственного Бюджетного Образовательного Учреждения Высшего Профессионального Образования «Московский Государственный Технический Университет Гражданской Авиации» (МГТУ ГА) Кафедра АРЭО КОНТРОЛЬНАЯ РАБОТА ПО ДИСЦИПЛИНЕ «МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ» . Тема контрольного задания: Обработка опытных данных по результатам многократных измерений. Вариант 3 При сверлении 80 отверстий одним и тем же сверлом и последующим измерением диаметров отверстий получены данные (в мм), приведены частоты контрольных измерений диаметров отверстий. Таблица 1
Требуется: Результаты измерений записать в виде вариационного ряда. Составить интервальный статистический ряд распределения частот и частостей (относительных частот) измеренных значений диаметров отверстий. Построить гистограмму и полигон частостей, сделать вывод о предполагаемом законе распределения измеренных диаметров отверстий. Вычислить среднее арифметическое и среднее квадратическое отклонение. Найти точечные оценки параметров нормального закона распределения, записать плотность вероятности и функцию распределения измеренных значений. Найти теоретические частоты нормального закона распределения, проверить согласие эмпирической функции распределения с нормальным законом с помощью критерия χ² Пирсона при уровне значимости α = 0,05. Найти интервальные оценки для среднего арифметического при α = 0,10; 0,05. 1. Результаты измерений запишем в виде вариационного ряда.
2. Составим интервальный статистический ряд распределения частот и частостей (относительных частот) измеренных значений диаметров отверстий. В учебных целях можно принять k = 6. Ширину интервала определяем по формуле 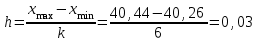 мм ммРассчитаем границы интервалов: x0= xmin = 40,26 ; x1 = x0 +h = 40,26 + 0,03 = 40,29 ; x2 = x1 +h = 40,29 + 0,03 = 40,32 ; x3 = x2 +h = 40,32 + 0,03 = 40,35 ; x4 = x3 +h = 40,35 + 0,03 = 40,38 ; x5 = x4 +h = 40,38 + 0,03 = 40,41 ; x6 = xmах = 40,44 . m1= 2 +1 + 2 = 5; m 2 = 3+5 + 6 = 14; m 3 = 7+7 + 11 = 25; m 4 = 9+6 + 7 = 22; m 5= 3+4 + 3 = 10; m 6 = 2+1 + 1 = 4; m1 / n = 5/80 = 0,0625; m2 / n = 14/80 = 0,175; m3 /n = 25/80 = 0,3125; m4 /n = 22/80 = 0,275; m5 /n = 10/80 = 0,125; m6 /n = 4/80 = 0,05; n = 80– количество измеренных отверстий.
3. Построим гистограмму и полигон частостей. Площадь прямоугольника равна частости данного частичного интервала. Высота прямоугольника равна mi/nh, где h – ширина интервала. 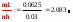 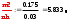 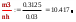 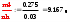 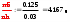 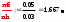 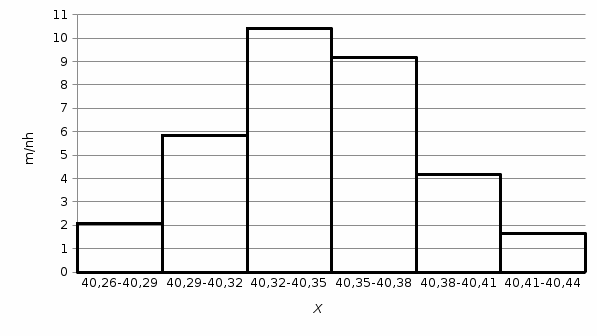 Рис. 1. Гистограмма частостей 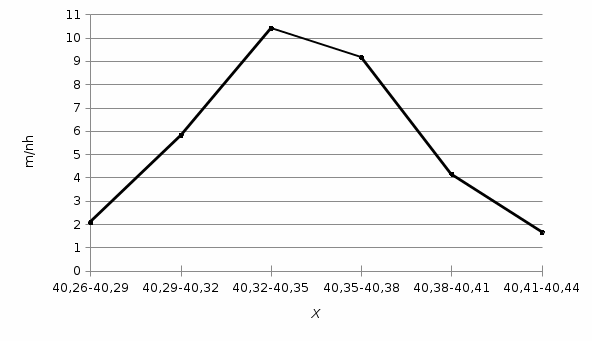 Рис. 2. Полигон частостей Вывод: По виду гистограммы и полигону частостей делаем предположение о нормальном законе распределения измеренных диаметров отверстий, так как центр распределения один и находится в интервале ]40,32-40,35], кривая распределения сначала возрастает, затем убывает. 4. Вычислим среднее арифметическое и среднее квадратическое отклонение. Среднее арифметическое определяем по формуле: 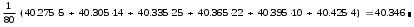 Среднее квадратическое отклонение равно:  5. Найдём точечные оценки параметров нормального закона распределения, запишем плотность вероятности и функцию распределения измеренных значений. Точечные оценки параметров нормального закона распределения находим методом моментов. Они равны: 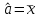 = 40,34 = 40,34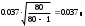 Запишем функцию плотности вероятности и функцию распределения измеренных значений 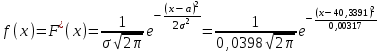 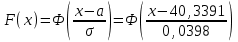 6. Найдём теоретические частоты нормального закона распределения, проверить согласие эмпирической функции распределения с нормальным законом с помощью критерия χ² Пирсона при уровне значимости α = 0,05. Для определения теоретических частот нормируем интервалы, т.е. выражаем их в единицах среднего квадратического отклонения 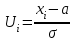 . При этом минимальное значение U1 заменяем на - . При этом минимальное значение U1 заменяем на -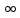 , а максимальное значение U6 – на + , а максимальное значение U6 – на +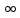 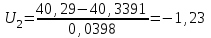 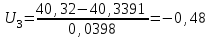 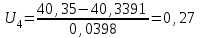 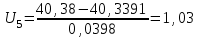 Вероятность попадания случайной величины х с параметрами а и σ в частичные интервалы находим по формуле 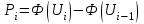 и таблице приложения 1: и таблице приложения 1: P1= Ф(-1,23) - Ф(- 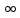 ) = - 0,3907 + 0,5 = 0,1093 ) = - 0,3907 + 0,5 = 0,1093P2= Ф(-0,48) - Ф(-1,23) = - 0,1844 + 0,3907= 0,2063 P3= Ф(0,27) - Ф(-0,48) = 0,1064 + 0,1844 = 0,2908 P4= Ф(1,03) - Ф(0,27) = 0,3485 - 0,1064= 0,2421 P5= Ф(+ 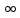 ) - Ф(1,03) = 0,5 - 0,3485 = 0,1515 ) - Ф(1,03) = 0,5 - 0,3485 = 0,1515Вычисляем теоретические частотыnpi и наблюдаемое значение статистики по формуле 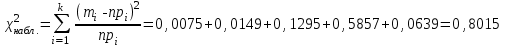 Таблица 4
По таблице квантилей 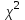 - распределения (Приложение 2 [1]) по заданному уровню значимости α = 0,05 и числу степеней свободы ν = k – r –1 = 5 – 2 – 1 = 2, где k = 5; r = 2 – число параметров функции распределения, находим критическое значение - распределения (Приложение 2 [1]) по заданному уровню значимости α = 0,05 и числу степеней свободы ν = k – r –1 = 5 – 2 – 1 = 2, где k = 5; r = 2 – число параметров функции распределения, находим критическое значение 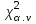 = 5,991. = 5,991. Вывод: Так как 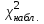 = 0,8015 < = 0,8015 <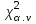 = 5,991, то эмпирической функция распределения согласуется с нормальным законом распределения. = 5,991, то эмпирической функция распределения согласуется с нормальным законом распределения.7. Найдём интервальные оценки для среднего арифметического при α = 0,10; 0,05. Найдём доверительный интервал для оценки среднего арифметического 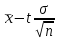 < <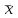 < <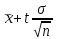 где 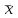 = 40,3391, σ = 0,0398; n = 80. = 40,3391, σ = 0,0398; n = 80. Значения квантилей Стьюдента в зависимости от числа степеней свободы ν = n – 1 = 79 и уровня значимости α/2 = 0,05 и 0,025 находим в Приложении 3 [1] t =1,645 и 1,96. Получаем доверительные интервалы: 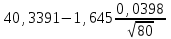 < <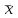 < <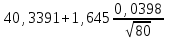 ; ; 40,3318 < 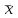 < 40,3464 при α = 0,10 < 40,3464 при α = 0,10С вероятностью 0,9 можно ожидать, что средний диаметр отверстий в генеральной совокупности будет находиться в интервале от 40,3318 мм до 40,3464 мм. 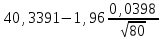 < <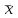 < <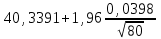 ; ; 40,3304 < 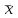 < 40,3478 при α = 0,05. < 40,3478 при α = 0,05.С вероятностью 0,95 можно ожидать, что средний диаметр отверстий в генеральной совокупности будет находиться в интервале от 40,3304 мм до 40,3478 мм. Вывод по работе: величина диаметр отверстий распределена по нормальному закону со средним значением 40,34 мм и средним квадратическим отклонением 0,04 мм. Список литературы 1. Логвин А.И., Иванов В.В. Метрология, стандартизация и сертификация. Пособие к изучению дисциплины и выполнению контрольного задания. – М.: МГТУ ГА, 2004. – 32 с. 2. Логвин А.И., Епифанцева Д.А. Метрология, стандартизация и сертификация: Пособие по проведению практических занятий для студентов всех специальностей всех форм обучения. – М.: МГТУ ГА, 2006. – 28 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||