электроника. Кафедра конструирования электронных средств
 Скачать 3.45 Mb. Скачать 3.45 Mb.
|
2.2 Сравнение различных тыльных контактовПроизводительность моделируемых солнечных элементов увеличивается с увеличением работы выхода, но после определенного значения она насыщается. С увеличением работы выхода металла высота барьера уменьшается из-за изгиба зон на границе раздела металл-полупроводник. По мере того как работа выхода металла увеличивается, Voc становится больше. Следовательно, эффективность солнечного элемента перовскита также возрастает. Энергетически невыгодно, чтобы дырки продвигались к электрону, потому что электрическое поле вблизи HTM тыльного контакта станет отрицательным. По этой причине можно ожидать, что более низкая рабочая функция ответственна за более низкую эффективность Для подтверждения адекватности и точности результатов моделирования была создана модель солнечного элемента в программе SCAPS-1D со структурой ITO / TiO2 (50 нм) / CH3NH3PbI3-xClx (400 нм) / Spiro-OMeTAD (250 нм) / Au и проведено сравнение результатов моделирования её характеристик с экспериментальными данными, представленными в работе [21]. Результаты моделирования показывают близкое совпадение с экспериментальными данными Таблица 2.6 - Теоретические и экспериментальные параметры солнечных элементов
3. Моделирование характеристик и параметровсолнечных элементов3.1 Численный метод моделированияМетод конечных разностей является дискретным приближением вычисления подхода к дифференциальному уравнению, его результаты расчетов не являются непрерывной функцией, кроме приближенного значения функции в каждой точке сетки. Основная идея метода конечных разностей заключается в использовании различных коэффициентов для замены производной части в уравнениях. При моделировании, это предполагает, что толщина перовскита составляет L нм, и дискретизируется [0, L] с расстоянием h. Схема устройства показана на Рисунке 3.1.  Рисунок 3.1 - Схема устройства На основе дискретизации модели устройства, уравнение Пуассона и уравнение непрерывности в дискретной форме могут быть описаны как: 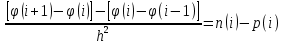 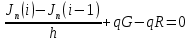 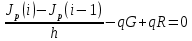 где, k = 1,2, 3, ..., N-1, i= 1, 2, ..., N, k является средней точкой между i-1 и I, N-координаты точки в сетке. Подход предполагает, что изменением электрического поля, подвижностью носителей и плотностью тока можно пренебречь между I и i+1, так что уравнения преобразуются в: 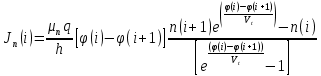 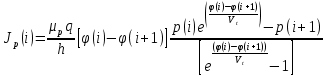 Есть 3 × (N - 2) неизвестные (n, p, φ) после подстановки в уравнение примут вид: 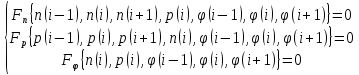 В результате чего получаем нормальные граничные условия, которые позволяют провести численное моделирование. Jn, Jp, а также R являются нелинейными функциями, так что уравнения являются нелинейными. Необходимо привести эти уравнения к линейному виду. Согласно теории итерационного метода, когда одна переменная рассчитывается, как мы предполагаем, то и другие переменные константы. Таким образом, когда мы вычисляем φ, она должна содержать n и p как константы. Используя разложение в ряд Тейлора по 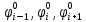 , то уравнение можно переписать в виде: , то уравнение можно переписать в виде: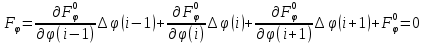 Для того, чтобы обеспечить сходимость и точность результатов, отношения между φ, а также n и р необходимо учитывать в следующем виде: 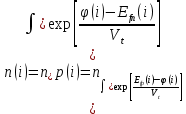 Каждый коэффициент из уравнения показан ниже: 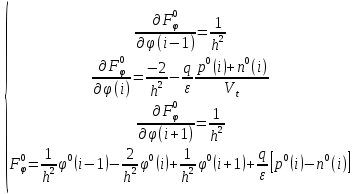 Использованный метод выбран потому, что коэффициенты матрицы очень малы, и некоторые из них приблизительно равны нулю. Кроме того, эта матрица соответствует граничным условиям выбранного метода решения. Решенное уравнение Пуассона удовлетворяет условию точности. После получения новых значений потенциала, подставим их в уравнение непрерывности для вычисления n и p соответственно. Когда n рассчитано, φ и p считаются константами. Используя разложение в ряд Тейлора по 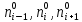 уравнение приобретает вид: уравнение приобретает вид: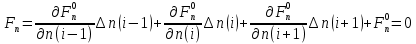 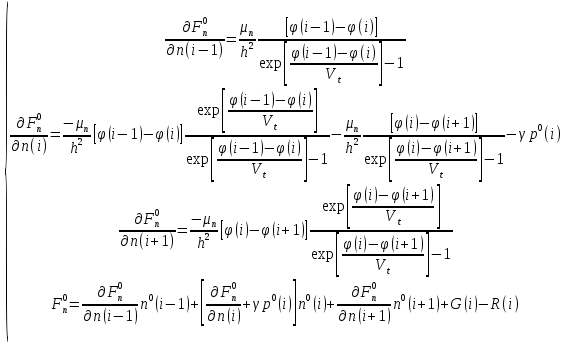 Уравнение с разложением в ряд Тейлора может быть получено с использованием того же подхода, как было показано ранее. Результаты показаны в уравнениях ниже. 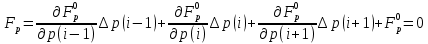 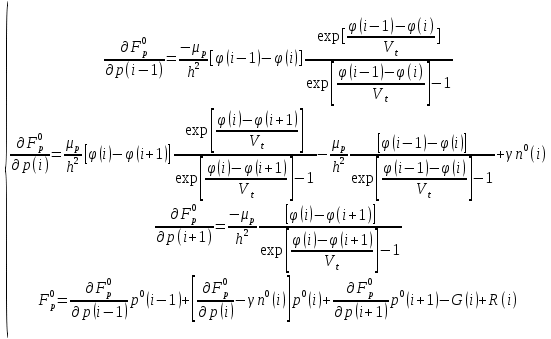 После решения уравнений непрерывности, необходимо оценить удовлетворяют ли n и p условию точности. Если эти вычисления отвечают условию точности, цикл итерации останавливается и 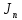 и и 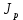 рассчитываются. Новые значения плотности (n и p) подставляются в уравнение Пуассона, и новая итерация не проводится до тех пор, пока все решения отвечают условию точности. Схема последовательности операций итерационного показана на Рисунке 3.2. рассчитываются. Новые значения плотности (n и p) подставляются в уравнение Пуассона, и новая итерация не проводится до тех пор, пока все решения отвечают условию точности. Схема последовательности операций итерационного показана на Рисунке 3.2.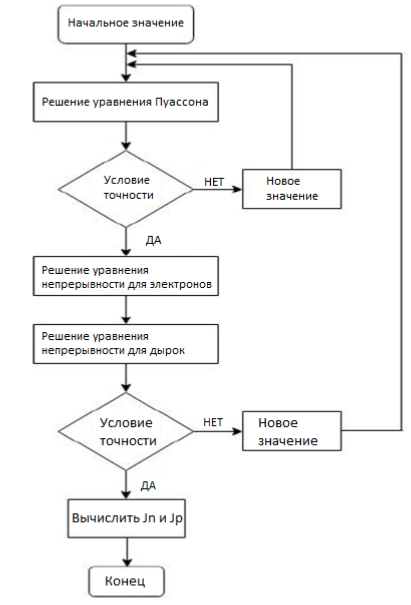 Рисунок 3.2 - Схема последовательности операций итерационного метода |
