электроника. Кафедра конструирования электронных средств
 Скачать 3.45 Mb. Скачать 3.45 Mb.
|
1.6 Отжиг в муфельной печиМуфельные печи - это термические печи, имеющие съемные камеры из высокотемпературного сплава, которые работают в защитной атмосфере. Обычно в коробчатом виде, высококачественные печи для термообработки, способные работать при высоких температурах до 1800℃. Муфельные печи могут использоваться для различных применений, включая закалку, волочение, отжиг, пайку, спекание и снятие напряжений как в воздухе, так и в контролируемой атмосфере. 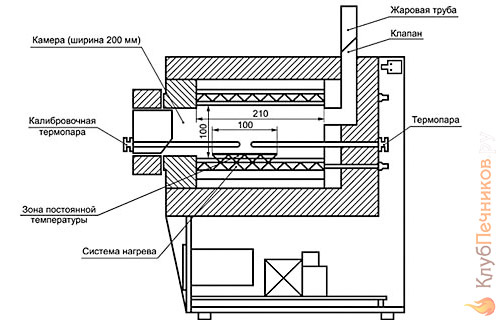 Рис.1.10 – Устройство муфельной печи Главная составляющая муфельной печи – это муфель, который изготавливается чаще всего из керамики. Этот материал является универсальным для изготовления печи разного рода. Вокруг муфеля наматывается обогревательный элемент в виде проволоки и замазывается это керамической обмазкой. Вокруг муфеля располагается теплоизоляционный материал и все это обшивается металлическим корпусом из листа металла толщиной 1,5-2 мм. Так как нагрев печи начинается вокруг муфеля, то достичь больших температур (выше 1150 градусов) не получается. В связи с этим производители разработали специальный волокнистый материал для изготовления муфеля, который позволяет располагать нагревательные элементы изнутри. Это дает возможность увеличить температурный предел муфельных печей. Но недостатком волокнистого материала является его недолговечность: под действием газовых испарений, солей и масел от нагреваемого материала волокно разрушается. Для более равномерного нагрева рабочей камеры некоторые производители встраивают вентиляцию. А для вывода продуктов сгорания существует вытяжной механизм, который через трубу выводит дым и пар из печи. Для контроля и регулирования температуры в печи используется электронный терморегулятор, который соединяется с нагревателем и термопарой. Терморегулятор позволяет контролировать не только температуру, но и время выдержки изделия в печи. Причем эти показатели имеют очень высокую точность, особенно в лабораторной муфельной печи, ведь от их значения и полученного результата зависит точность проводимых исследований. 1.7 Теоретические основы численного моделированияЧисленное моделирование предназначено для изучения эффективности солнечных элементов [17]. Ученые определили самый эффективный метод чтобы исследовать перенос носителей заряда. Проблема кремниевых солнечных элементов решается путем решения уравнения непрерывности Пуассона для электронов и дырок с 1975 года [18]. Несколько видов программного обеспечения широко используется для тонкопленочных солнечных элементов, среди них SCAPS-1D, PC1D и AMPS-1D. Модель кремниевых солнечных элементов можно рассматривать как р-n-переход с легированием, и он использует плотность и распределение легирующей примеси, чтобы описать производительность солнечных элементов [19]. Для преобразователей цифровых сигналов, уровень окислительно-восстановительных процессов в электролитах влияет на выходное напряжение устройства, так что граничные условия и начальное значения берутся на его основе [20]. В модели солнечного элемента на основе перовскита, выходное напряжение определяется разностью между уровнем энергии квази-Ферми для электронов и дырок на два электрода устройства [21]. Поэтому для того, чтобы получить точные результаты, плотность носителей и их потенциал может быть выражены с помощью модели энергетического уровня квази-Ферми. Кроме того, граничные условия и начальное значение должны быть созданы с помощью модели уровня энергии квази-Ферми. Одномерная модель вычисляется с помощью уравнения Пуассона и уравнения непрерывности. Последствия дефектов плотности и ионизированная плотность легирования не рассматриваются в этой модели, поэтому уравнение Пуассона могут быть заданы: 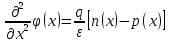 (1.6) (1.6)где φ - потенциал, d - элементарный заряд, ε – диэлектрическая проницаемость, n - плотность свободных электронов, р – плотность свободных дырок. Непрерывность уравнений электронов и дырок может быть описано: 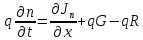 (1.7) (1.7)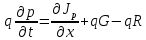 (1.8) (1.8)где 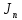 - плотность тока электронов, - плотность тока электронов, 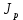 - плотность тока дырок, G –скорость оптической генерации, R - скорость рекомбинации. - плотность тока дырок, G –скорость оптической генерации, R - скорость рекомбинации.Уравнения непрерывности можно упростить следующим образом: 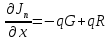 (1.9) (1.9)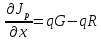 (1.10) (1.10)В перовскитных солнечных элементах, выходной ток включает в себя диффузионный ток и дрейфовый ток, вызванный электронами и дырками. Он может быть получен из следующих уравнений: 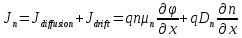 (1.11) (1.11)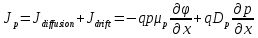 (1.12) (1.12)где 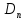 - коэффициент диффузии электронов, - коэффициент диффузии электронов, 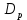 - коэффициент диффузии дырок, - коэффициент диффузии дырок, 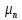 - подвижность электронов, и - подвижность электронов, и 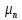 - подвижностью дырок. В этой модели, предполагается, что - подвижностью дырок. В этой модели, предполагается, что 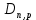 , а также , а также 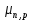 удовлетворяют соотношению Эйнштейна, которое может быть выражено как: удовлетворяют соотношению Эйнштейна, которое может быть выражено как: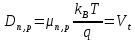 (1.13) (1.13)где 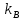 - постоянная Больцмана, T - температура. - постоянная Больцмана, T - температура.Есть три неизвестных, которые нужно найти, это n, р, а также φ. Для того, чтобы получить эти значения, необходимо выбрать соответствующие граничные условия. На катоде и аноде, плотность электронов и дырок подчиняются распределению Больцмана, и они могут быть выражены как: 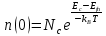 (1.14) (1.14)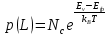 (1.15) (1.15)в котором, 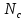 - плотность состояния, - плотность состояния, 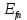 , а также , а также 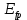 являются электронами и являются электронами идырками уровня Квази-Ферми. В перовскитных солнечных элементах, выходное напряжение равно разности между 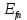 и и 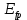 , и может быть выражено как: , и может быть выражено как: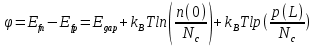 Для того, чтобы упростить модель, предполагается, что значение выходного напряжения является зонной энергией, и соответствующие граничные условия могут быть заданы: 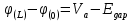 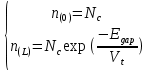 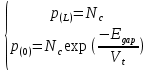 где, 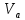 - приложенное напряжение. - приложенное напряжение.В 2004 году ученые показали, что, если толщина устройства является достаточно небольшой (при 100 нм), то экспоненциальная зависимость поглощения света и расстояния не влияют на производительность устройства значительно, так что скорость генерации может быть установлена в качестве постоянной [22]. Таким образом, используя экспоненциальную модель, можно определить скорость генерации заряда по формуле: 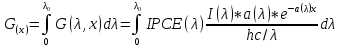 (1.6) (1.6)где, IPCE - движение фотона, 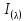 - плотность падающего света, - плотность падающего света, 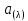 - коэффициент поглощения, h - постоянная Планка, c - это скорость света, λ - длина волны фотона. - коэффициент поглощения, h - постоянная Планка, c - это скорость света, λ - длина волны фотона.Таким образом, скорость генерации заряда можно переписать в виде: 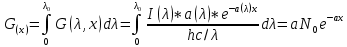 где, 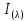 - является AM1.5 в солнечном спектре, который рассчитывается по - является AM1.5 в солнечном спектре, который рассчитывается поNREL, 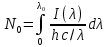 Таким образом, результат будет выглядеть так: 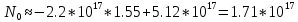 В устройстве, все носители будут двигаться к их соответствующему электроду, и когда они приходят в движение, электроны и дырки будут рекомбинировать. Есть два вида механизма рекомбинации, прямой и косвенный. Прямая рекомбинация обусловлена прямым переходом электронов между зоной проводимости и валентной зоной. Как правило, он используется для описания устройства с низкой концентрацией дефектов. Может быть выражен как [23]: 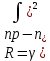 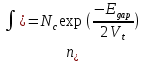 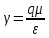 где γ - коэффициент рекомбинации, 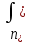 - собственная концентрация носителей. - собственная концентрация носителей.Косвенная рекомбинация используется для описания устройства с высокой концентрацией дефектов. Это может быть выражено как [18]: 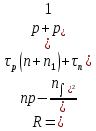 где, 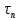 - время жизни электрона, - время жизни электрона, 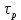 - время жизни дырки. В разрабатываемой модели низкая концентрация дефектов, поэтому рассматриваем только прямой механизм рекомбинации. - время жизни дырки. В разрабатываемой модели низкая концентрация дефектов, поэтому рассматриваем только прямой механизм рекомбинации. |
