Методика. курсовая методика математика улучшенная. Кафедра математики и методики обучения математике методика обучения учащихся тождественным преобразованиям рациональных выражений
 Скачать 319.54 Kb. Скачать 319.54 Kb.
|
Типичные ошибки учащихся при работе с тождественными преобразованиями и рекомендации по их устранениюРаздел «Тождественные преобразования» занимает основное место в школьном курсе математики. Изучение тождественных преобразований имеет самостоятельное значение, т.к. связан со следующими вопросами: обобщение операций над числами, проведение вычислений «в общем виде», обучение применению алгебраической символики; классификация и определение алгебраических выражений, преобразование выражений к стандартному виду; рационализация выражений. тождественные преобразования играют роль вспомогательного «инструмента» при решении уравнений и неравенств, при исследовании функций и ряде других тем школьного курса математики. тождественные преобразования имеют значимое воспитательное значение, т.к. они способствуют развитию у учащихся операционного мышления, воспитанию таких качеств личности, как целеустремленность в поиске решения, сообразительность, аккуратность, честность, справедливость. Самая типичная ошибка учащихся состоит в том, что они при решении уравнений и неравенств без дополнительных пояснений используют преобразования, которые нарушают равносильность, приводящую к потере или появлению корней. Значимая группа ошибок заключается в том, что учащиеся не уделяют должного внимания нахождению области определения выражений, хотя конкретно она в ряде случаев есть ключ к решению. Разнообразие тождественных преобразований усложняет понимание цели, которая является конечной при работе с выражениями. Неточное понимание целевого преобразования отрицательно отражается на осознании предназначения и служит источником множественных ошибок. Этот факт указывает на то, что педагогу необходимо включать разъяснение конкретных целей при выполнении всех тождественных преобразований, что является составной частью методики обучения. Для управления этим процессом преподаватель обязан уметь давать чёткие характеристики сущности допущенных учащимися ошибок. Наличие точности помогает учащимся найти подходящие действия для дальнейшей работы по осуществлению тождественных преобразований выражений [6]. Типичные ошибки учащихся при работе с тождественными преобразованиями: Смешивают правила умножения степеней с правилом возведения в степень ( 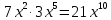 ). ).Распространяют по неверной аналогии правила умножения степеней с одним основанием на случай умножения степеней с разными основаниями ( 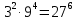 ). ).Складывают показатели степеней при сложении степеней – смешивают с правилом умножения степеней ( 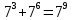 ). ).Неправильно применяют формулы (по неверной аналогии: 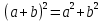 или lg ( или lg (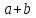 )= lg )= lg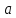 +lg +lg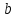 , или , или 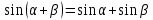 ). ).Сокращают в алгебраической дроби по неверной аналогии не множители, а слагаемые ( 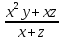 = = 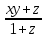 ). ).Изменяют знак не у всех членов вычитаемого, когда вычитается многочлен и, тем более дробь. Не учитывают знак подкоренного выражения при использовании свойства арифметического корня и получают под корнем отрицательное число. Одним из типов ошибок является неправильное применение формул, составим ряд упражнений для того, чтобы в дальнейшем была возможность исключить эти ошибки. Представь в виде произведения: 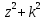 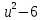 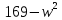 Проверь верность равенства: 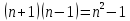 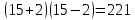 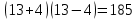 Упростите выражение: 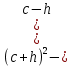 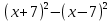 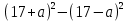 Упростите выражение: 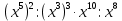 , при x=-3 , при x=-3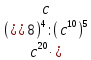 , при c=5,5 , при c=5,5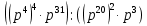 , при p=4 , при p=4Доказать, что если r – нечётное число, то 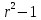 делится на 4. делится на 4.Основные приёмы по устранению ошибок в дальнейшем в это типе является планомерное оттачивание формул, с разбором на конкретных примерах, также можно включить создание примеров по аналогии с уже решаемыми. Рекомендации по устранению типичных ошибок. При изначальном знакомстве с тождественными преобразованиями необходимо, чтобы учащиеся проговаривали каждый шаг, выполняя преобразования и учились формулировать правила и законы необходимости применения того или иного преобразования. Учащихся необходимо проинформировать, что при применении тождественных преобразований алгебраических выражений используют два правила: постановки и замены равным данному выражению. Учащихся необходимо научить определять области применимости изучаемых тождеств. При изучении тождественных преобразований учитель должен давать чёткие формулировки, демонстрировать аналитические записи. Учитель должен научить учащихся использовать подходящий алгоритм для тождественных преобразований Учителю необходимо научить детей проводить преобразования в прямом и обратном порядке. Учащиеся должны знать о приложениях. Учащиеся должны научиться использовать тождественные преобразования в комплексе с другими. ЗаключениеВ процессе обучения курсу математики учащиеся многократно встречаются с выражениями и учатся работать с различными их видами. Впервые учащиеся встречаются с понятием тождественных преобразований на уроках алгебры в 7 классе. В первую очередь вводится понятие тождественно равных выражений. Тождественное преобразование выражения – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному. Часто это определение используется в сокращенном виде, в котором опускается слово «тождественное». Предполагается, что мы в любом случае проведём преобразование выражения таким образом, чтобы получить выражение, тождественное исходному. В процессе рассмотрения данной темы мы изучили возможность применения тождественных преобразований в зависимости от вида выражений, подробно рассмотрели виды выражений, алгебраических и неалгебраических (трансцедентных). Алгебраические выражения включают в себя только те выражения, которые содержат такие действия над переменными, как сложение, вычитание, умножение, деление, извлечение корня, возведение в степень с рациональным показателем. Неалгераические выражения, в которых содержатся переменные под знаками lg, sin, cos, tg, со знаком модуля, с операциями возведения в степень с иррациональными показателями. Провели исследование по тождественным преобразованиям разных классов выражений. Тождественные преобразования представляют собой работу, которую мы проводим с числовыми и буквенными выражениями, а также с выражениями, которые содержат переменные. Все эти преобразования мы проводим для того, чтобы привести исходное выражение к такому виду, который будет удобен для решения задачи. Основные виды тождественных преобразований мы рассмотрим в этой главе. По итогам исследования составили список типичных ошибок учащихся при работе с тождественными преобразованиями и подготовили список рекомендаций, чтобы исправить их в процессе обучения, таким образом, достигли цели исследования и решили все поставленные задачи. список использованных источниковАктуальные вопросы теории и методики обучения математике в средней школе: сборник научный статей. Вып. 1. – Киров: Изд-во ВятГГУ, 2011. – 111 с. Барыбин К.С. Методика преподавания алгебры: Пособие для учителя.− М.: Просвещение, 2006.− 345 с. Блох А.Я. О тождественных преобразованиях в курсе алгебры VI-VIII кл. [Текст] / Метод.рекомендации и указания по методике преподавания математики в средней школе: Сб. статей / А.Я. Блох. - М.: МГПИ им. В.И. Ленина, 2005.− 83 с. Виленкин ۛ Н.Я. Равенства, тождества, уравнения, неравенства Н.Я. Виленкин, С.И. Шварцбурд// Математика в школе. - 2000. - № 4. Виленкин Н.Я. и др. Современные основы школьного курса математки.— М.: Просвещение, 2001.− 240 с. Груденов Я.И. Совершенствование методики работы учителя математики: Кн. для учителя. — М.: Просвещение, 1990. — 224 с. Давыдов В.В. Теория развивающего обучения [Текст]/ В.В.Давыдов. – М., 1996. – 544 с. Канин Е.С. К формированию умений и навыков в вычислениях и тождественных преобразованиях / Е.С. Канин// Математика в школе. − 2002. − №5. Колмогоров А.Н. и др. Алгебра и начала анализа: Учебное пособие для 9 и 10 классов средней школы / Под ред. А. Н. Колмогорова.− М.: Просвещение. 2015.− 384 с. Колмогоровۛ А.Н., Абрамов А.М., Дудницын Ю.П., Ивлиев Б.М., Шварцбурд С.И. Алгебра и начала анализаۛ Учеб.для 10– 11 кл. сред. шк.−М.: Просвещение, 2010. − 320 с. Колягин Ю.М., Луканин Г.Л. Основные понятия современного школьного курса математики.− М.: Просвещение, 2014. −367 с. Кондрушенко Е.М. Тождественные преобразования выражений в школьном курсе математики.— Великий Новгород: МОУ ПКС «Институт образовательногомаркетинка и кадровых ресурсов», 2006. — 72 с. Мoрдкович А.Г. Алгебра. 7 кл.: в 2 ч. Ч.1: Учеб.для общеобразоват. учреждений / А.Г. Мордкович. - М.: Мнемoзина, 2013. – 240 с. Мoрдкович А.Г. Алгебра. 8 кл.: учебник для классов с углубленным изучением математики / А.Г. Мордкович. - М.: Мнемозина, 2013. −228 с. Теоретические основы обучения математике в средней школе [Текст]: учебное пособие/ Т.А. Иванова, Е.Н. Перевощикова, Т.П. Григорьева, Л.И. Кузнецова; Под ред. проф. Т.А. Ивановой. - Н. Новгород: НГПУ, 2010 − 320 с. Тождественные преобразования выражений. Математика. 8-9 кл./ М.В. Шабанова, О.Л. Безумова, С.Н. Котова и др. – М.: Дрофа. 2010.− 77 с. |
