Методика. курсовая методика математика улучшенная. Кафедра математики и методики обучения математике методика обучения учащихся тождественным преобразованиям рациональных выражений
 Скачать 319.54 Kb. Скачать 319.54 Kb.
|
мЕТОДИКА ОБУЧЕНИЯ УЧАЩИХСЯ ТОЖДЕСТВЕННЫМ ПРЕОБРАЗОВАНИЯМ РАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙРазличные трактовки понятия тождества. Виды тождественных преобразованийТождественные преобразования предполагают собой работу, которая проводится с числовыми и буквенными выражениями, а также с выражениями, содержащими переменные. Все эти преобразования производятся для того, чтобы привести исходное выражение к такому виду, который будет удобным для решения задачи. Основные виды тождественных преобразований мы рассмотрим в этой главе. Впервые учащиеся встречаются с понятием тождественных преобразований на уроках алгебры в 7 классе. Впервые вводится понятие тождественно равных выражений. Тождественное преобразование выражения – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному выражению [16]. Посмотрим на наглядном примере: Используем для замены выражения 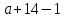 тождественно равное ему выражение тождественно равное ему выражение 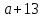 и проведём тождественное преобразование выражения и проведём тождественное преобразование выражения 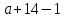 . .Рассмотрим форму записи выражений при проведении тождественных преобразований. Обыденная запись исходного и полученного в ходе преобразования выражения в виде равенства. Запись 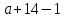 = = 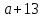 означает, что выражение означает, что выражение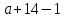 было приведено к виду было приведено к виду 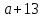 . . Последовательное выполнение действий приводит нас к цепочке равенств, которая состоит из нескольких расположенных по порядку тождественных преобразований. Запись 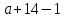 = = 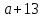 = 13 + = 13 + 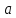 Мы наблюдаем последовательное проведение двух преобразований: в первую очередь выражение 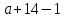 привели к виду привели к виду 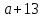 , а затем – к виду 13 + , а затем – к виду 13 + 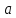 . .Ряд выражений, которые мы начинаем изучать в 8 классе, имеют смысл не при всех значениях переменных. Проведение тождественных преобразований в этих случаях требует от нас внимания к области допустимых значений переменных (ОДЗ). Выполнение тождественных преобразований может оставлять ОДЗ постоянной или же сужать ее. Сужение либо расширение области допустимых значений переменных во время выполнения тождественных преобразований имеет общее значение при решении задач, так как может воздействовать на точность проведения вычислений и привести к возникновению ошибок. Выделим виды тождественных преобразований, с которыми учащимся приходится встречаться чаще всего, в группу основных тождественных преобразований. Также помимо основных тождественных преобразований существует ряд преобразований, которые относятся к выражениям конкретного вида. Для дробей – это приемы сокращения и приведения к новому знаменателю. Для выражений с корнями и степенями - это все действия, выполненные на базе свойств корней и степеней. Для логарифмических выражений действия, проводимые на основе свойств логарифмов. Для тригонометрических выражений все действия, в которых использованы тригонометрические формулы [3]. Рассмотрим основные тождественные преобразования. Перестановка местами слагаемых, множителей. В первую очередь рассмотрим перестановку местами слагаемых. С этим тождественным преобразованием учащиеся встречаются чаще всего. Основное правило: в любой сумме перестановка слагаемых местами не отражается на результате. Данное правило сформировано на переместительном и сочетательном законах сложения. Эти свойства дают возможность нам переставлять слагаемые местами и получать при этом выражения, тождественно равные исходным. Именно поэтому перестановка слагаемых местами в сумме является тождественным преобразованием. В качестве слагаемых в сумме могут выступать не только числа, но и выражения. Их точно так же, как и числа, можно переставлять местами, не влияя на конечный результат вычислений. Приведём пример. В сумме трех слагаемых 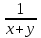 + ( + (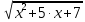 + + 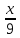 ) ) 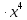 + (-24) + (-24) 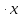 слагаемые можно переставить, например, в таком порядке: слагаемые можно переставить, например, в таком порядке:(-24) 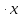 + + 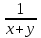 + ( + (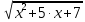 + + 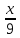 ) ) 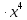 . Также можно переставить местами слагаемые в знаменателе дроби . Также можно переставить местами слагаемые в знаменателе дроби 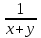 и при этом дробь примет вид и при этом дробь примет вид 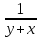 , а выражение под знаком корня , а выражение под знаком корня 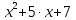 тоже является суммой, в которой можно менять местами слагаемые. тоже является суммой, в которой можно менять местами слагаемые.Таким образом, множители в выражениях можно менять местами и получать тождественно верные уравнения, сформулируем конкретнее: в произведении перестановка множителей местами не влияет на конечный результат. Сформировано данное правило на переместительном и сочетательном законах умножения, которые подтверждают истинность тождественного преобразования. Раскрытие скобок. Скобки могут содержать записи числовых выражений и выражений с переменными. Данные выражения можно преобразовать в тождественно равные выражения, не имеющие скобок или же имеющие их в меньшем количестве. Этот способ преобразования выражений называют раскрытием скобок. Приведём пример. Раскрыть скобки в выражении 5(p-2q+4t)=5p-10q+20t Группировка слагаемых, множителей. В случаях, когда выражение содержит три, и более слагаемых, необходимо использовать такие тождественные преобразования как группировка слагаемых. Данный способ преобразований предполагает объединение нескольких слагаемых в группу путем их перестановки и заключения в скобки. При проведении группировки слагаемые меняются местами таким образом, чтобы группируемые слагаемые оказались в записи выражения рядом. Впоследствии их можно заключить в скобки. Сгруппированные слагаемые и множители, могут быть представлены как простыми числами, так и выражениями. Замена разностей суммами, частными произведениями и обратно. Замена разностей суммами стала возможна благодаря знакомству учащихся с противоположными числами. Теперь вычитание из числа 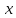 числа числа 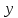 учащиеся могут рассмотреть как прибавление к числу учащиеся могут рассмотреть как прибавление к числу 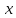 числа числа 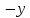 . Равенство . Равенство 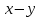 = = 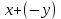 можно считать справедливым и на его основе проводить замену разностей суммами. можно считать справедливым и на его основе проводить замену разностей суммами.Переход к суммам осуществляется от любых разностей. Аналогично учащиеся могут произвести обратную замену. Замена деления на умножение на число, обратное делителю, становится возможной исходя из понятия взаимно обратных чисел. Данное преобразование записывается: 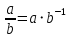 . .Это правило было положено в основу правила деления обыкновенных дробей. Рассмотрим на примере. Частное 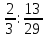 можно заменить произведением вида можно заменить произведением вида 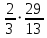 . .Аналогично, деление может быть заменено умножением. Замена умножения делением поводится по схеме 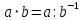 . .Выполнение действий с числами. Выполнение действий с числами подчиняется правилу порядка выполнения действий. Во-первых, проводятся действия со степенями чисел и корнями из чисел. Во-вторых, проводится замена логарифмов, тригонометрических и прочих функций на их значения. В-третьих, производятся действия в скобках. Затем, можно проводить все остальные действия слева направо. Важно помнить, что умножение и деление проводят до сложения и вычитания. Действия с числами дают возможность преобразовать исходное выражение тождественное равное ему [2]. Приведём пример. Необходимо преобразовать выражение 7 ⋅ ( 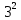 − 2) ⋅ − 2) ⋅ 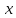 + + 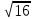 ⋅( ⋅(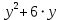 ), выполнив все действия с числами. ), выполнив все действия с числами. Первым делом обращаем внимание на степень 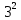 и корень и корень 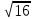 и вычислим их значения: и вычислим их значения: 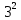 = 9 и = 9 и 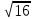 = = 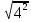 =4. =4. Подставим полученные значения в исходное выражение и получим: 7 ⋅ (9 − 2) ⋅ 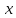 + 16 ⋅ ( + 16 ⋅ (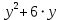 ) . ) . Далее произведём действия в скобках: 9 − 2 = 7. И перейдем к выражению 7 ⋅ 7 ⋅ 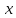 + 24⋅ ( + 24⋅ (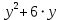 ). ).Остаётся выполнить умножение чисел 7 и 7. Получаем: 49 ⋅ 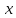 + 4 ⋅ ( + 4 ⋅ (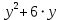 ). ).Действиям с числами могут предшествовать иные виды тождественных преобразований, в том числе группировка чисел или раскрытие скобок. При работе с числовыми выражениями, нашей целью будет являться нахождение значения выражения. Если же мы преобразуем выражения с переменными, то целью наших действий будет упрощение выражения. Вынесение за скобки общего множителя. В примерах, где слагаемые в выражении имеют одинаковый множитель, учащимся следует выносить этот общий множитель за скобки. Для выполнения этого действия в первую очередь необходимо представить данное выражение как произведение общего множителя и выражения в скобках, состоящее из исходных слагаемых без общего множителя. В числовом выражении 27⋅7 + 3⋅27 учащиеся выносят общий множитель 27 за скобки и получают тождественно верное выражение вида 27⋅ (7+ 3). Приведение подобных слагаемых. Данный вид тождественных преобразований относится к суммам, содержащим подобные слагаемые. Допустимы два варианта: суммы, содержащие одинаковые слагаемые и суммы, отличающиеся числовым коэффициентом слагаемых. Действия с суммами, содержащими подобные слагаемые, являются приведением подобных слагаемых. Его выполнение проводится так: учащиеся выносят общую буквенную часть за скобки и проводят вычисление суммы числовых коэффициентов в скобках. Например, 7 + 9 ⋅y − 5 ⋅ y. Целесообразно вынести буквенную часть y за скобки и получить выражение 7 + y ⋅ (9 − 5) После этого стоит провести вычисление значения выражения в скобках и получить сумму вида 7 + y ⋅ 4. Замена чисел и выражений тождественно равными им выражениями. Исходное выражение, состоящее из чисел и выражений, можно заменять тождественно равными им выражениями. Такое преобразование исходного выражения приводит к тождественно равному ему выражению. Рассмотрим на примере: 9 + 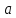 , число 9 можно заменить суммой 6 + 3, так учащиеся получат выражение (6 + 3) + , число 9 можно заменить суммой 6 + 3, так учащиеся получат выражение (6 + 3) +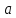 , тождественно равное исходному выражению. , тождественно равное исходному выражению.Прибавление и вычитание одного и того же числа. Прибавление и одновременное вычитание одного и того же числа или выражения является искусственным приемом преобразования выражений. Приведём пример: 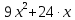 Учащиеся прибавляют и отнимают от него число шестнадцать, что позволяет в последующем провести ещё одно тождественное преобразование – выделить квадрат двучлена: 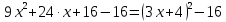 |
