Методика. курсовая методика математика улучшенная. Кафедра математики и методики обучения математике методика обучения учащихся тождественным преобразованиям рациональных выражений
 Скачать 319.54 Kb. Скачать 319.54 Kb.
|
Методические аспекты обучения тождественным преобразованиям выражений в курсе алгебры основной школыОсновные понятия и содержание области тождественных преобразований в курсе алгебры основной школыВ школьном курсе алгебры содержится четыре основных раздела – это число, функции, уравнения и неравенства, а также тождественные преобразования. Изучение тождественных преобразований учащиеся начинают в начальной школе и продолжают в течение всего курса математики, которая перетекает в алгебру. В первой части нашей работы мы рассмотрим основные понятия, которые являются ключевыми при изучении тождественных преобразований. В число этих математических понятий входят: понятия «выражение», «тождественно равные выражения», «тождество» и основное понятие, в изучаемой теме, «тождественные преобразования выражений» [5]. Рассмотрим все понятия по порядку, чтобы увидеть связующие звенья в процессе обучения тождественным преобразованиям выражений. Выражением в математике называют запись, состоящую из чисел, букв (обозначающих a постоянные или переменные величины), знаков a математических действий. Математическим выражением называют запись, состоящую из чисел, букв, которыми обозначают постоянные и переменные величины, знаков математических действий. В школьной программе по математике существует два класса выражений: алгебраические и неалгебраические (трансцендентные). Алгебраическое выражение состоит из конечного числа букв и цифр, соединенных знаками действий (сложение, умножение, вычитание, деление, извлечения корня и возведение в целую степень). Трансцендентными выражениями называются аналитические функции, которые не являются алгебраическими (логарифмические, тригонометрические, и показательные) [11]. Так как выражения – это предмет нашего исследования, то в любом из этих классов можно выделить следующие подклассы математических выражений. К алгебраическим выражениям относятся: целые рациональные выражения: одночлены; многочлены (первой, второй, третьей степени); дробные рациональные выражения; иррациональные выражения. К неалгебраическим (трансцедентным) выражениям относятся: тригонометрические выражения: показательные выражения; логарифмические выражения. Существует огромное количество подходов к понятию «тождества». При абсолютно всём разнообразии словесных формулировок понятий тождества, тождественного преобразования двух выражений, тождественного равенства двух выражений можно выделить лишь три подхода, которые рассматриваются следующими определениями. Равенство, верное при любых значениях переменных, называется тождеством. Выражения, связанные знаком тождественного равенства, называют тождественно равным. Приведём пример: 𝑎 + 𝑏 = 𝑏 + 𝑎, 𝑎𝑏 = 𝑏𝑎 Это определение формулируется в 7 классе впервые. Замену одного выражения другим, ему тождественно равным, называют тождественным преобразованием этого выражения [15]. Это определение допускает пропуск слово «тождественное» и произносят только «преобразование выражения», но в понимании понятие тождественные преобразования. Определение достаточно кратко сформулировано и наиболее удобно при рассмотрении целых рациональных чисел, но используя его, мы не сможем называть тождественными все равенства, которые на первый взгляд подходят под определение. Приведем пояснительные примеры: Выражение 19𝑥 + 32 – 9 можно заменить тождественно равным ему выражением 19𝑥 + 23, то есть мы выполняем тождественное преобразование выражения 19𝑥 + 32 − 9 = 19𝑥 + 23 [10]. Заменяем в выражении 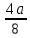 выражением выражением 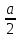 , что отражает тождественные преобразования, то есть , что отражает тождественные преобразования, то есть 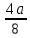 = = 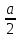 . .Выражение x не является тождественным преобразованием выражения 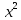 , так как выражения x и , так как выражения x и 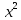 не тождественно равные. не тождественно равные.Равенство, верное при всех допустимых значениях переменных, называется тождеством. Допустимыми значениями переменных в этом случае являются все значения переменных, при которых имеет смысл правая и левая части данного равенства. Тождественное преобразование одного выражения в другое и тождественное равенство двух выражений, определяется по аналогии с первым случаем [4]. Замеченные недостатки первого определения не найдены во втором. Приведём пояснительные примеры: lga + lgb = lg (ab) 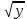 - -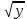 =0 =0Этому определению удовлетворяют приведённые примеры, в отличие от первого определения, но существует ряд недостатков. Главной ценностью тождеств является возможность заменять одно выражение другим, при условии того, что они тождественны, а по второму определению вытекает, что равенства 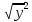 = =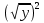 и и 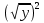 =у – тождества, а вот равенство =у – тождества, а вот равенство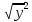 = у не будет являться тождеством. = у не будет являться тождеством.Используя многие неравенства, которые являются тождествами, по второму определению, можно привести решение уравнения к неравносильному решению. Равенство, верное при любых значениях переменной (пар значений переменных, троек значений переменных и т. д.), принадлежащих данному множеству, называется тождеством на этом множестве. Замена одно выражение другим, тождественно равным ему на данном множестве, называют тождественным преобразованием этого выражения на указанном множестве. Это определение является наиболее точным и не имеет недостатков, можно прийти к выводу, что при решении заданий имеет место обращения именно к этому определению. Каждая область знаний, в которой используются математические данные, испытывает время от времени потребность в упрощении методов решений заданий, и использует замену одного выражения другим как вынужденную меру для упрощения, т.е. используется метод тождественных преобразований [3]. Начальные знания о тождественных преобразованиях выражений учащиеся получают в начальной школе, а углубленное и систематизированное изучение этого вопроса начинается в 7 классе основной школы в программе изучения курса алгебры. В 7 классе учащиеся получают полноценное представление о целых рациональных выражениях (одночленах и многочленах). В 8 классе учащиеся изучают дробные выражения (дробные рациональные выражения, арифметические квадратные корни). В 9 и 10 классах учащиеся получают представление об иррациональных выражениях (степени с рациональными показателями, корни n-ной степени). 10 класс знакомит детей с тригонометрическими выражениями, а 11 с логарифмическими. Заменяя одно выражение на более удобное или более простое, мы находим решение задачи, то есть требуется провести тождественные преобразования выражений и упростить решение. |
