Рис.2 Схемы передач
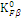 ψd ψd
|
Твердость зубьев колеса НВ
|
Коэффициент для схемы передачи (рис.2)
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
0,4
|
≤350 >350
|
2,01 1,53
|
1,67 1,34
|
1,46 1,23
|
1,27 1,13
|
1,16 1,08
|
1,09 1,05
|
- -
|
- -
|
0,6
|
≤350 >350
|
2,47 1,75
|
2,01 1,53
|
1,74 1,38
|
1,46 1,23
|
1,26 1,14
|
1,16 1,08
|
1,08 1,06
|
- -
|
0,8
|
≤350 >350
|
- -
|
- -
|
2,01 1,53
|
1,62 1,32
|
1,41 1,21
|
1,31 1,16
|
1,21 1,08
|
1,08 1,04
|
1,0
|
≤350 >350
|
- -
|
- -
|
2,28 1,67
|
1,82 1,42
|
1,6 1,31
|
1,46 1,23
|
1,31 1,16
|
1,16 1,08
|
1,2
|
≤350 >350
|
- -
|
- -
|
2,54 1,81
|
2,04 1,53
|
1,8 1,42
|
1,6 1,31
|
1,46 1,23
|
1,23 1,11
|
1,4
|
≤350 >350
|
- -
|
- -
|
- -
|
2,28 1,67
|
2,01 1,53
|
1,74 1,5
|
1,6 1,31
|
1,32 1,16
|
1,6
|
≤350 >350
|
- -
|
- -
|
- -
|
- -
|
2,23 1,67
|
2,01 1,53
|
1,74 1,38
|
1,46 1,23
|
коэффициент ψd=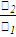 = =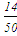 =0,28 =0,28
При ψd≤0,4 и схеме передач определим начальный коэффициент концентрации нагрузки K0Fβ. В нашем случае выбираем схему 6
K0Fβ=1,09
Режимы нагружения
|
0
|
I
|
II
|
III
|
IV
|
V
|
X
|
1,000
|
0,750
|
0,500
|
0,400
|
0,315
|
0,200
|
X - коэффициент режима нагрузки
Выбираем Х=0,750
Коэффициент KFβ при переменной нагрузке вычисляем по формуле:
KFβ=K0Fβ(1-x)+x=1,09*(1-0,75)+0,75=1,02
Степень точности
|
Твердость Зубьев колеса НВ
|
Коэффициент KFυ для прямых зубьев при окружной скорости υ, м/с
|
|
|
1
|
2
|
4
|
6
|
8
|
≥10
|
6
|
≤350
|
-
|
-
|
-
|
1,40
|
1,58
|
1,67
|
|
>350
|
-
|
-
|
-
|
1,11
|
1,14
|
1,17
|
7
|
≤350
|
-
|
-
|
1,33
|
1,50
|
1,67
|
1,80
|
|
>350
|
-
|
-
|
1,09
|
1,13
|
1,17
|
1,22
|
8
|
≤350
|
-
|
1,20
|
1,38
|
1,58
|
1,78
|
1,96
|
|
>350
|
-
|
1,06
|
1,12
|
1,16
|
1,21
|
1,26
|
9
|
≤350
|
1,13
|
1,28
|
1,50
|
-
|
-
|
-
|
|
>350
|
1,04
|
1,07
|
1,14
|
-
|
-
|
-
|
Так как значение окружной скорости υ=2,538 м/с лежит между значениями 2 и 4, коэффициент динамической нагрузки KFυ находим с помощью интерполяции
2
|
1,20
|
2,538
|
KFυ(?)
|
4
|
1,38
|
KFυ=1,20+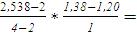 1,25; 1,25;
KFυ=1,25
|
 Скачать 1.28 Mb.
Скачать 1.28 Mb.