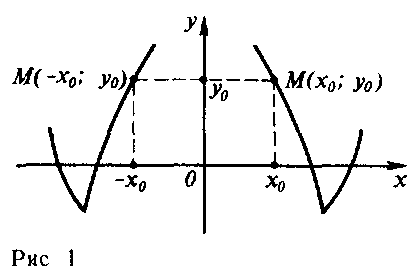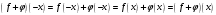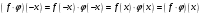Реферат по физической культуре. 911768 Реферат. Кафедра высшей математики Реферат по дисциплине Основы исследований в математическом образовании рациональные приемы научной работы

• Название: Кафедра высшей математики Реферат по дисциплине Основы исследований в математическом образовании рациональные приемы научной работы
• Анкор: Реферат по физической культуре
• Дата: 08.07.2021
• Размер: 286.37 Kb.
• Имя файла: 911768 Реферат.docx
• Тип: Реферат; #223754

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ПЕРМСКИЙГОСУДАРСТВЕННЫЙ ГУМАНИТАРНО-ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ» МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ Кафедра высшей математики
Реферат по дисциплине «Основы исследований в математическом образовании»
РАЦИОНАЛЬНЫЕ ПРИЕМЫ НАУЧНОЙ РАБОТЫ
	Работу выполнила студентка 131 группы Иванова Елена Петровна Подпись
Оценка за реферат	Проверила канд. пед. наук доц. Г.Г. Шеремет Подпись
Пермь ПГГПУ 2021

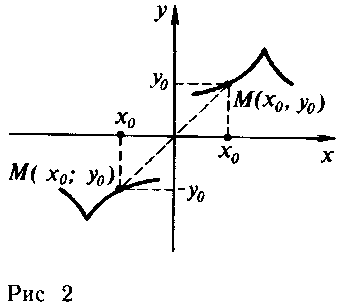
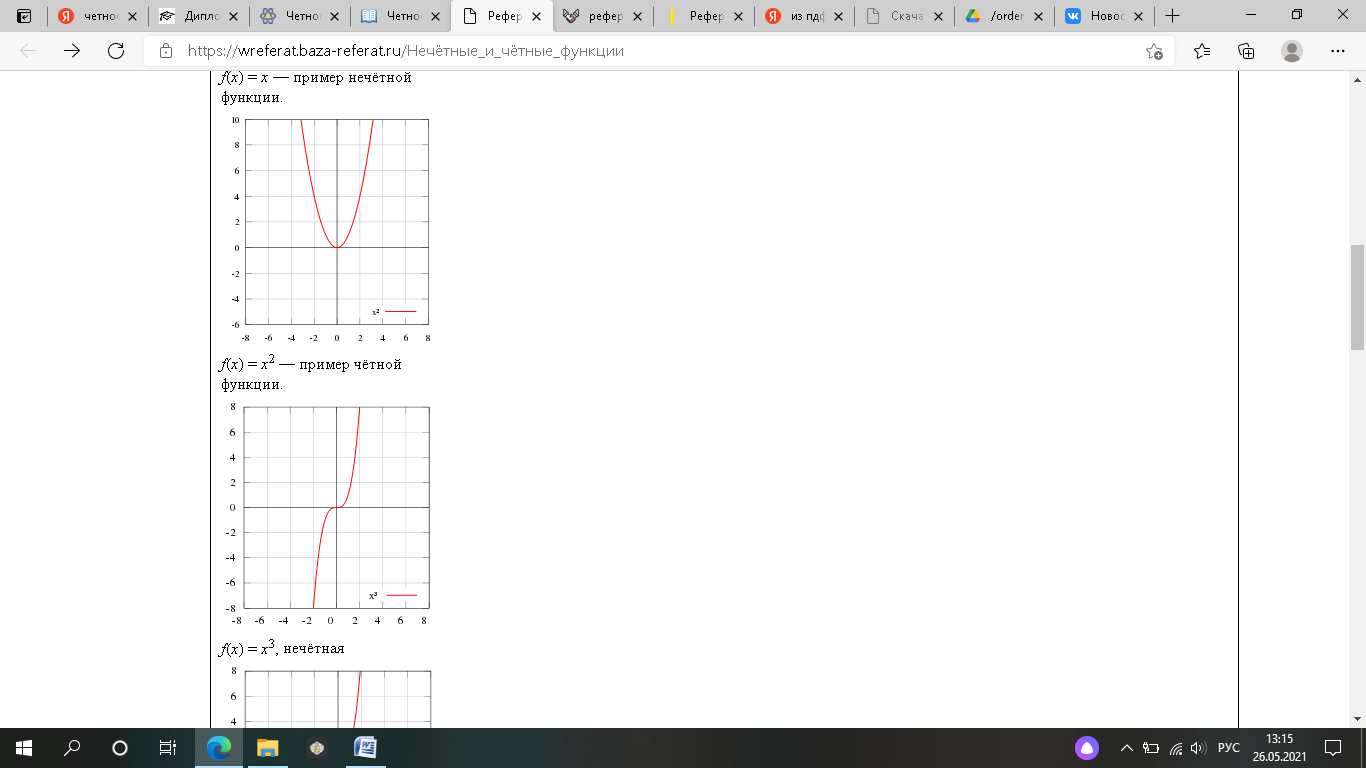
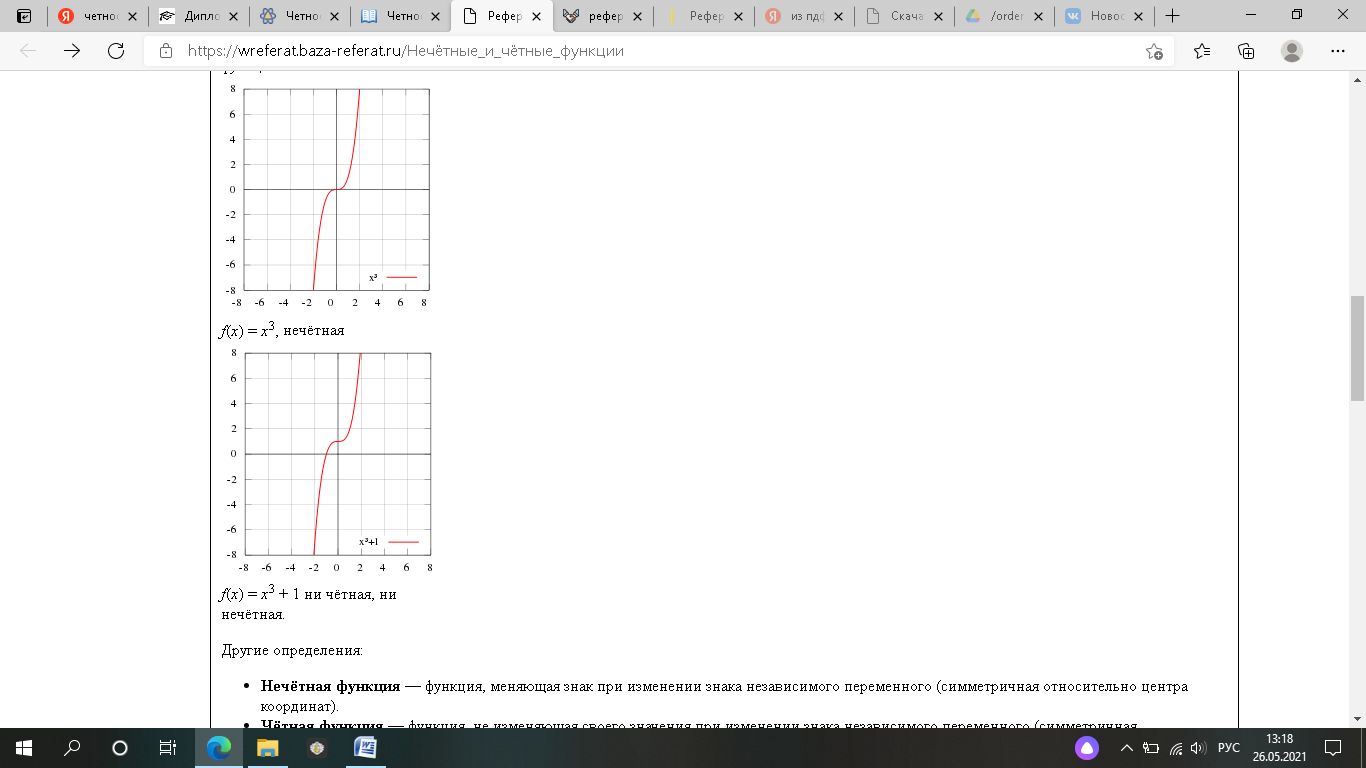
Содержание

Введение 3

1. Теоретические основы четной и нечетной функции 4

4

Рис. 1 – Пример нечётной функции 4

f(x) = x — пример нечётной функции. 4

4

Рис. 2 – Пример чётной функции 4

5

Рис. 3 – Пример ни чётной, ни нечётной функции 5

2. Определение чётной и нечётной функции. 5

3. Нечетные функции 6

4. Понятие ни чётной ни нечётной функции. 7

5. Применение чётности и нечётности в физике. 8

6. Свойства чётных и нечётных функций. 9

7. Доказательство некоторых свойств 9

8.Примеры исследования данной функции на чётность и нечётность. 11

9. Исследование на чётность и нечётность функции с помощью построения графика 13

10. Занимательные утверждения 14

Заключение 17

Список использованных источников 18

Введение

Термин «функция» ввел в математику Готфрид Лейбниц (1646-1716).Он употреблял его в очень узком смысле, связывая только с геометрическими образами.

Лишь И.Бернулли дал определение функции, свободное от геометрического языка: «Функцией переменной величины называется количество, образованное каким угодно способом преобразования этой переменной величины и постоянных».

Леонард Эйлер (1707-1783 гг.), вводя в своём учебнике понятие функции, говорил лишь, что «когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых».

В развитие понятия функции внесли свой вклад французский математик

Ж.-Б. Фурье (1768-1830 гг.), русский ученый Н.И. Лобачевский (1792-1856 гг.), немецкий математик Дирихле ( 1805-1859 гг.) и др. ученые, и общепризнанным стало следующее определение: « Переменная величина у называется функцией переменной величины х, если каждому значению величины х соответствует единственное определенное значение величины у».

1. Теоретические основы четной и нечетной функции

Нечётные и чётные функции — функции, графики которых обладают симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Такое название возникло как обобщение чётности степенных функций: функция f(x) = xn чётна тогда и только тогда, когда n чётно, и нечётна тогда и только тогда, когда n нечётно.

Рис. 1 – Пример нечётной функции

f(x) = x — пример нечётной функции.

Рис. 2 – Пример чётной функции

f(x) = x² — пример чётной функции.

Рис. 3 – Пример ни чётной, ни нечётной функции

f(x) = x³ + 1 ни чётная, ни нечётная. [1]

2. Определение чётной и нечётной функции.

Числовая функция у=f(х) называется четной, если:

1) область определения функции симметрична относительно точки О числовой оси (т. е. если точка x₀ принадлежит области определения функции, то и точка – x₀ также принадлежит области определения функции);

2) для любого значения независимой переменной, принадлежащего области определения функции, выполняется равенство

f(x)=f(–x). (1)

Примеры четных функций: у=с , у=х , у=|x| .

График четной функции на координатной плоскости Оху симметричен относительно оси ординат.

Докажем это. Если точка М с координатами (х, у) принадлежит графику функции f (рис. 1), т. е. f(x₀)=у₀, то, по определению четной функции, –x₀ D(f) и
f(–x₀)=y₀, а потому и точка М' с координатами (–x₀, y₀) принадлежит графику функции f. Но точка М' как раз симметрична точке М относительно оси Оу. Таким образом, вместе со всякой точкой М график четной функции f содержит и симметричную ей точку М', а это и означает, что этот график симметричен относительно оси ординат.



Рис. 4 – График чётной функции

Верно и обратное если график функции f симметричен относительно оси ординат, то функция f – четная.

3. Нечетные функции

Числовая функция y=f(x) называется нечетной, если:

1) область определения функции симметрична относительно точки О числовой оси (т. е. если точка х₀ принадлежит области определения функции, то и точка –х₀ также принадлежит области определения функции);

2) для любого значения независимой переменной, принадлежащего области определения функции, выполняется равенство [2]

f(-x)=–f(x). (1')

Примеры нечетных функций:y=x³, y=1/x, y=2x

График нечетной функции на координатной плоскости Оху симметричен относительно начала координат О.



Рис. 5 – График нечётной функции

Верно и обратное утверждение: если график функции f симметричен относительно начала координат, то функция f нечетная.

4. Понятие ни чётной ни нечётной функции.

Отметим, что «нечетная функция» – это отнюдь не то же самое, что «не четная функция» (т. е. функция, не являющаяся четной). Как правило, функция, «взятая наугад», не будет ни четной, ни нечетной график «произвольной» функции не обязан обладать какими либо свойствами симметрии

Пример 1. Функция f(х)=1/(х+1) не является ни четной, ни нечетной, поскольку для ее области определения D(f) = не выполнено условие симметрии: точка х₀=1 принадлежит D(f), а точка –х₀=–1 не принадлежит D(f).

Пример 2. Функция f(x)=х²+х+1 также не является ни четной, ни нечетной. Эта функция определена всюду, и поэтому условие симметрии для нее выполнено, однако ни условие четности, ни условие нечетности не выполнено. В самом деле, f(–x)=х²–х+1. Положив х=1, находим f(1)=1+1+1=3, f(–1)=1–1+1=1, и f(–1) не равно ни f(1), ни –f(1).

5. Применение чётности и нечётности в физике.

Физический пример

Если физическая система обладает какой–нибудь симметрией, то и связанные с нею функции часто имеют те или иные свойства симметрии. В простейших случаях возникают как раз четные или нечетные функции.

Пример. На горизонтальный стержень – ось Ох – надета однородная пружина, концы которой закреплены в симметричных точках



Рис. 5 – Горизонтальный стержень

x=–d, и х=d, а к середине пружины – в точке х=0 – прикреплена шайба, свободно (без трения) перемещающаяся вдоль стержня (рис. 3, а). Пусть шайба отведена в точку с координатой х. Обозначим через F(к) величину силы, действующей на шайбу со стороны пружины (точнее говоря, проекцию этой силы на ось Ох), а через U(х) – потенциальную энергию шайбы в этом положении. Очевидно, пружине безразлично, вправо или влево отводится шайба: абсолютная величина силы и потенциальная энергия при смещениях х и – х одинаковы, т. е.

|F(–х)|=|F(х)| и U(–x)=U(x).

Учитывая, что сила в положениях х и –х направлена в противоположные стороны (см. рис. 3.б, в), можем записать

F(–х)=–F(х).[1]

Таким образом, из одних лишь соображений симметрии мы получаем следующее:

1. 
   функция F(х), выражающая зависимость силы Fот смещения х, нечетная;
   
2. 
   функция U(х), выражающая зависимость потенциальной энергии от смещения, четная.
   

6. Свойства чётных и нечётных функций.

Теорема 1. Если f и w четные функции, то f+, f–, f∙ – четные функции.

Теорема 2. Если f и w нечетные функции, то f+, f– – нечетные функции, а f∙ – четная функция.

Теорема 3. Если функция f является четной (соответственно нечетной) и не равна нулю ни в одной точке, то функция 1/f также будет четной (соответственно нечетной).

7. Доказательство некоторых свойств

1). Сумма двух чётных функций чётна, а сумма двух нечётных функций нечётна.

Пусть функция f и  чётны и x D(f)∩D(). Тогда f(–x)=f(x), (–x)=(x), и потому



Значит функция f+ – чётная. Аналогично доказывается нечётность функции f+ в случае, когда f и  нечётные.

2). Произведение двух чётных функций является чётной функцией, равно как и произведение двух нечётных функций.

Произведение чётной и нечётной функции – нечётная функция.

Пусть функция f и  чётны, а x и x D(f)∩D(). Тогда имеем:



значит f∙ –чётная функция.

3). Очевидно, степенная функция f(х)=хⁿ, где п N, при четном п будет четной, а при нечетном n – нечетной (собственно, отсюда и появилась эта терминология). Произвольный многочлен р(х), вообще говоря, не будет ни четной, ни нечетной функцией. Однако его можно представить в виде суммы двух многочленов р₊ (х) и р_– (х), являющихся соответственно четной и нечетной функциями. Например,



где



– сумма одночленов из р(х), содержащих х в четной степени, а

р_– (х) = х⁷ – х⁵ + х

– сумма одночленов из р(х), содержащих х в нечетной степени.
Оказывается, что не только многочлен, но и любую функцию с симметричной областью определения можно представить в виде суммы четной и нечетной функции. [4]

4). Теорема. Если функция f удовлетворяет условию симметрии, то ее можно представить в виде суммы двух функций – четной f₊(х) и нечетной f_–(х)

f(x)=f₊(x)+f_–(x), (1)

области определения которых те же, что у функции f: D(f₊)=D(f_–)=D(f) причем такое представление единственно.

Доказательство. Допустим, что функция f(х) уже представлена в виде (1) и функции f₊и f_– удовлетворяют соотношениям

f+(-x)=f+(x), f-(-x)=-f-(x)

(2)

Подставив в формулу (1) вместо х значение – х, из формул (2) получим

f(-x)=f₊(-x)-f_–(-x), (3)

Складывая равенства (1) и (3), получаем

f(x)+f (-x)=2f₊(x),

откуда

(4а)

Аналогично, вычитая (3) из (1), находим

(4б)

Таким образом, если функция f представима в виде (1), то функции f₊ и f_– однозначно отыскиваются по функции f с помощью формул (4)

Следовательно, если представление (1) существует, то оно единственно.

Для произвольной функции f определим функции f₊ и f_– соотношениями (4)

Тогда из формул (4) следует, что, во–первых, f₊(x)+f_–(x)=f(х), те (1) выполняется, и, во–вторых, что функции f₊ и f_–являются, соответственно, четной и нечетной. Например, проверим условие нечетности для функции f_– . Для произвольного х имеем



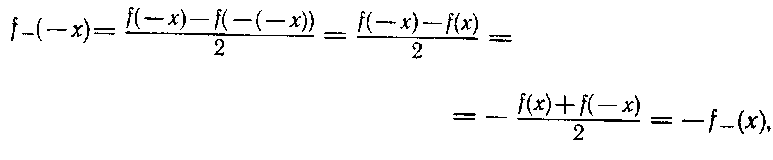
что и требовалось доказать Четность функции f₊ проверяется точно так же.

Замечание. Приведенное доказательство носит, как говорят, конструктивный характер: мы не только доказали существование и единственность представления (1), но и указали формулы (4), по которым можно найти четную и нечетную «части» данной функции.

8.Примеры исследования данной функции на чётность и нечётность.

Пример 1.

Доказать, что функция f(x)=3x²+x⁴ – чётная.

Решение

Область определения функции – все действительные числа. Она симметрична относительно числа 0.

f(–x)=3(–x)²+(–x)⁴=3x²+x⁴=f(x).

Пример 2

Доказать, что функция f(x)=

x3+x x2–1

–нечётная.

Решение

Область определения функции – все действительные числа, кроме 1 и –1:

D(f)=(–∞;–1)U(–1;1)U(1;+∞).

Очевидно, что область определения симметрична относительно числа 0.

f(–x)=

(–x)3–x (–x)2–1

=

–x3–x x2–1

=–f(x).

Пример 3

Проверить, является функция f(x)=–x²+xчётной или нечётной.

Решение

Область определения функции – все действительные числа. Она симметрична относительно числа 0.

f(–x)=– (–x)²+ (–x)=–x²–x.

Функция не является ни чётной, ни нечётной , так как ни одно из равенств из определения 1 и определения 2 не выполняется.

Пример 4

Функции f и g определены на множестве всех действительных чисел.

Является ли функция h(x) чётной или нечётной, если:

а) h(x) = f(x)g²(x), f и g – нечётные функции;

б) h(x) = f(x) + g(x), f и g – чётные функции.

Решение

а)h(–x)=f(–x)g²(–x)=–f(x).[–g(x)]²=–f(x)g²(x)=–h(x).

h(x) – нечётная функция.

б)h(–x)=f(–x)+g(–x)=f(x)+g(x)=f(x)+g(x)=h(x).

h(x)– чётная функция. [1]

9. Исследование на чётность и нечётность функции с помощью построения графика

Построить график функции y=2|log₂(3|x|-1)|+1

Построение [3]



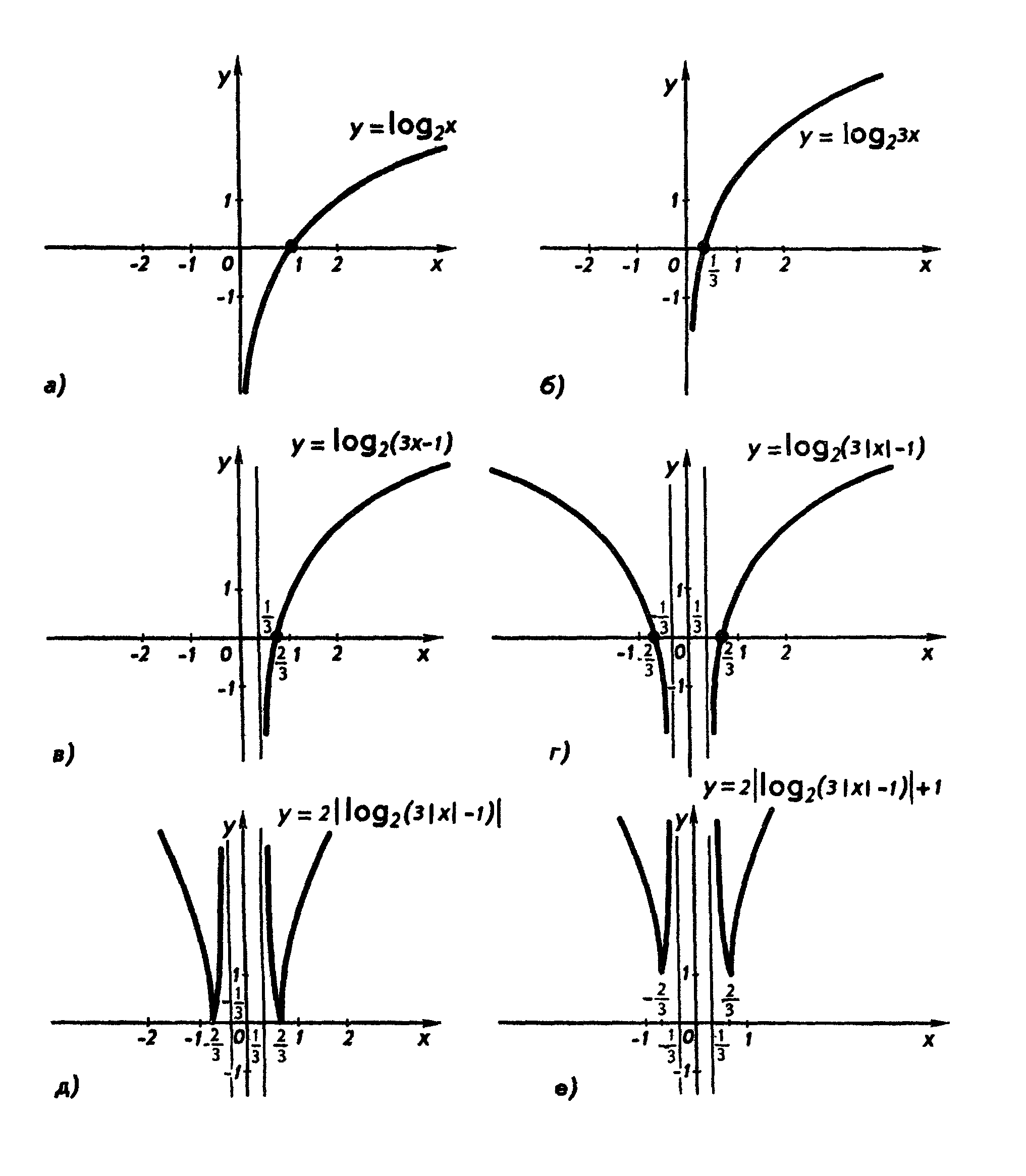
Рис. 6 – График функции

Вывод: график функции симметричен относительно оси ординат значит заданная функция чётная.

10. Занимательные утверждения

1.Сумма (разность) четных функций четна, а нечетных – нечетна.

2.Произведение или частное двух нечетных функций четно.

3.Произведение или дробь двух четных функций четно.

4.Произведение или дробь четной и нечетной функции нечетно.

5.Композиция двух четных функций четна.

6.Композиция двух нечетных функций нечетна.

7.Композиция любой функций с четной четна (но не наоборот)

8.Функция, обратная четной, четна, а нечетной – нечетна.

9.Производная четной функции нечетна, а нечетной – четна.

То же верно про производную третьего пятого и вообще любого нечетного порядка.Производная четного порядка сохраняет четность.

Докажем утверждения под номером 7 и 9.

№7.

Дано:

y= f(x) и y= g(x)-четная функция.

Доказать:

y=f (g(x))- четная функция.

Доказательство:

Так как g(x)-четная функция, то g(-x)=g(x) , следовательно f(g(-x))= f(g(x)), что и требовалось доказать

№9

Дано:

f (x)-четная функция.

Доказать:

f /(x)-нечетная функция/

Доказательство:

f /(-x)=(f(-x))/(-x)/=f/ (x)(-1)=-f /(x) [2]

Что и требовалось доказать.

Как правило, функция, взятая «наугад», не будет ни четной, ни нечетной. Возникает вопрос: зачем вводить понятия четности и нечетности, если «большинство» функций таковыми не являются?

Ответ на этот вопрос мы нашли в статье А.Землякова «Четные и нечетные функции», где он приводит два примера: физический и математический:

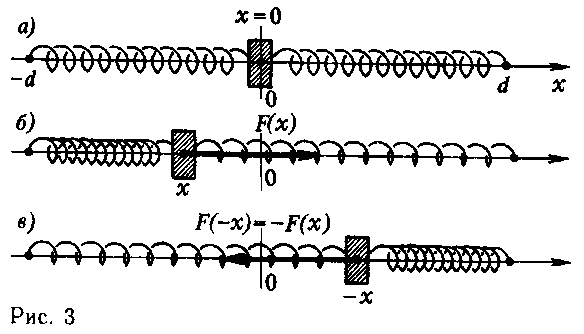
Физический:

На горизонтальный стержень – ось Ох – надета однородная пружина, концы которой закреплены в симметричных точках x=-d и x=d, а к середине пружины – в точке x=0 – прикреплена шайба, свободно (без трения) перемещающаяся вдоль стержня.

а) Пусть шайба отведена в точку с координатой x. Обозначим через F(x) величину силы, действующей на шайбу со стороны пружины (точнее говоря, проекцию этой силы на ось Ох), а через U(x)-потенциальную энергию шайбы в этом положении. Очевидно, пружине безразлично, вправо или влево отводится шайба: абсолютная величина силы и потенциальная энергия при смещениях x и –x одинаковы, то есть

и U(x) =U(-x)

Учитывая, что сила в положениях x и –x направлена в противоположные стороны (рис б, в), можем записать F(-x)=-F(x).

Таким образом, из одних лишь соображений симметрии мы получаем следующее:

1)Функция F(x), выражающая зависимость силы F от смещения x, нечетная;

2)Функция U(x),выражающая зависимость потенциальной энергии от смещения, четная.

Математический:

Очевидно, степенная функция f(х)= хn, где n N, при этом четном n будет четной, а при нечетном n – нечетной. Произвольный многочлен p(x), вообще говоря, не будет ни четной, ни нечетной функцией. Однако его можно представить в виде суммы двух многочленов

p+(x) и p--(x), являющихся соответственно четной и нечетной функциями.

Например:

p(x)= х7+2х6-х5-3х4-13х2+х+17= p+(x) + p-(x),где

p+(x)= 2х6-3х4-13х2+17 - сумма одночленов из p(x), содержащих х в четной степени, а

p-(x)= х7-х5+х - сумма одночленов из p(x), содержащих х в нечетной степени.

Оказывается, что не только многочлен, но и любую функцию с симметричной областью определения можно представить в виде суммы четной и нечетной функции.

Заключение

Анализ функции на четность и нечетность — распространенный тип задач.

Однако операция требует определенных знаний, поскольку очень часто возникают ситуации, в которых трудно принять верное решение.

Специалисты рекомендуют использовать специальный алгоритм, позволяющий без ошибок произвести исследование. Для его реализации следует приобрести соответствующие базовые знания.

Теперь следует сформулировать список базовых знаний, которые необходимы для анализа выражений на четность. Если нужно выполнить другие процедуры исследования, то его следует расширить.

Например, для нахождения максимума следует ознакомиться с производной. Необходимый минимум знаний о функциях следующий:

Область определения — D (f).

Виды.

Правила.

Свойства для четных и нечетных.

Классификация.

И, теперь, благодаря проведенному исследованию, мы обладаем всеми перечисленными выше компетенциями.

Список использованных источников

1. 
   Алгебра и математический анализ для 10 класса: Учеб. пособие для учащихся шк. и кл. с углубл. изуч. математики / Н. Я. Виленкин, О. С. Ивашев-Мусатов, С. И. Шварцбурд. — 6-е изд. — М.: Просвещение, АО "Московские учебники", 1999,— 336 с.: ил.
   
2. 
   Интернет-ресурс: nauka.club Режим доступа: https://nauka.club/matematika/algebra/chetnost-i-nechetnost-funktsi.html (дата обращения: 26.05.2021);
   
3. 
   Интернет-ресурс: studylib.ru. Режим доступа: //studylib.ru/docmanager.html?id=6297778&justuploaded=yes (дата обращения: 26.05.2021);
   
4. 
   Карп А. П. Даю уроки математики... : кн. для учителя : из опыта работы. — М. : Просвещение, 1992. — 192 с. — Рекоменд. лит.: с. 184—191.