Курсовая. Как показано в таблице 1, ZnSiP2 проявляет псевдокубическое упругое поведение
 Скачать 175.58 Kb. Скачать 175.58 Kb.
|
|
Константы упругости характеризуют способность материала деформироваться при малых напряжениях и затем возвращаются к его исходной форме после того, как напряжение прекращается. Константы упругости относятся к применяемым внешним силам, описанные напряжением, к результирующей деформации, описанной тензором деформации. Эластичное поведение асимметричного материала характеризуется 21 независимыми константами упругости, в то время как для изотропного материала это число констант уменьшается до двух. Между этими границами необходимое число констант зависит от симметрии материала. Четырехугольный кристалл имеет шесть независимых коэффициентов упругости; C11, C12, C13, C33, C44 и C66, и кубическая система имеет три независимые константы упругости; C11, C12 и C44. Расчетная однокристаллическая константа упругости для тетрагональной формы ZnSiP2 при 0 ГПа также приведена в таблице 1. Необходимо отметить, что в литературе отсутствуют экспериментальные данные, для того чтобы было можно сравнить с нашими результатами. Как видно из таблицы 1, текущие расчетные значения констант упругости отличаются в значительной степени из полученных Нойманом и вычисленных Вермой и коллегами [42,43]. Эти теоретические расчеты монокристаллических упругих констант все еще ждут экспериментального подтверждения. Структура халькопирита исследуемого материала характеризуется высоким значением констант C11 и C33, которые представляют собой сопротивление сжатию по основному направлению а и касис соответственно. Значения C11 и C33 выше примерно в два раза больше, чем у C44, C66, C12 и C13, которые представляют сопротивление сдвигу; Это свидетельствует о большем сопротивлении структуры халькопирита для ZnSiP2 к сжатию, чем к сдвигу. Как показано в таблице 1, ZnSiP2 проявляет псевдокубическое упругое поведение. Так как C11/C33 = 1,03, C12/C13 = 0,91 и C44/C66 = 1,03 (кубические системы характеризуются C11 = C33 ± C12 = C13 ± C44 = C66 ± 1). Следовательно, небольшая упругая анизотропия как при сжатии, так и при сдвиге. Характеризует халькопиритную фазу ZnSiP2. Обычно такое поведение наблюдается во многих тройных соединениях с халькопиритом или родственной структурой [44,45] вследствие, возможно, небольшого u и g деформации. Используя данные монокристаллического Cij, можно оценить линейную сжимаемость вдоль основной оси решетки. Для четырехугольной структуры линейная сжимаемость va и Vc по оси a- и c соответственно приведены в константах упругости по следующим соотношениям [46]: 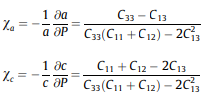 Расчетные линейные характеристики va и vc для ZnSiP2 очень близки; Va = 3,86 104 GPa1 и va = 4 104 GPa1. От Va и Vc, можно получить объем сжимаести, которая определяется как v = V1 o V/o P = 2va vc. Найдено v = 11,85 103 GPa1 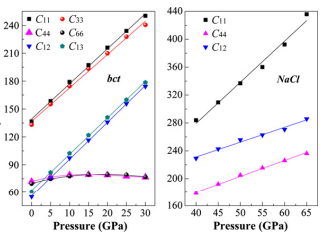 Рис. 3. Расчетная зависимость давления монокристаллических упругих констант Cij для как халькопиритной (bct), так и роксальтовой (NaCl) фазы ZnSiP2. Сплошные линии: Линейные посадки точек данных (для случая C44ðPÞ и C66ðPÞ фазы халькопирита, Сплошные линии являются наименьшими квадратными полиномами второго порядка точек данных) Модуль объема определяется как обратная объемная сжимаемость; B = v1 = 84,31 Гпа. Это значение В близко к значению, полученному из Береза-Murnaghan (ЭОС), соответствующая (B = 86,3 Гпа). Механическая стабильность требует, чтобы монокристаллический коэффициент упругости , Cij, должен удовлетворять определенным отношениям, известным как критерии стабильности, которые для тетрагональной структуры приведены ниже [46]:  Так же как и для кубической структуры: Полученные константы упругости для тетрагональной структуры ZnSiP2 удовлетворяют критериям стабильности, что указывает на их механическую стабильность. Однако, как показано в таблице 1, для структуры каменной соли не соблюдаются критерии устойчивости Born; (C11 C12) < 0 и C44 < 0. Поэтому можно сделать вывод, что ZnSiP2 механически неустойчива в каменной соли. Это хорошо согласуется с результатами, полученными от структурного исследования. Далее мы изучим влияние давления на эластичность ZnSiP2 как в халькопиритной, так и в роксальтовой фазах. Изменение их монокристаллических констант упругости по отношению к давлению показано на рис. 3. Монотонное увеличение расчетных параметров упругости с увеличением давлением в рассматриваемом диапазоне наблюдалось для двух фаз. Исключение составляют C44 и C66 для структуры халькопирита, которая начинает уменьшаться, когда давление превышает 20 и 25 ГПа соответственно для C44 и C66. Численные данные дополняются линейной посадкой методом наименьших квадратов, и полученные коэффициенты зависимости давления приведены в таблице 2. В не содержащем текстуры поликристаллическом материале монокристаллическую зернистость ориентируют случайным образом. В больших масштабах такие материалы могут считаться квазиизотропным или изотропным в статистическом смысле [48]. Единственный способ вычислить поликристаллические константы упругости из вычисления ab initio предназначены для вычисления монокристаллических констант упругости Cij, а затем для преобразования этих данных в макроскопические величины с помощью подходящих методов усреднения на основе статистической механики. Полностью описана изотропная система Эти две величины получают специальным усреднением отдельных констант упругости Cij. Существует несколько различных схем такого усреднения. В настоящей работе мы использовали усреднение Вогт-Рейсс-Хилл методом [49–53]. Таблица 2 Рассчитано первым (a) и вторым методами(b/2, в 102 GPa1) Производные давления монокристаллов Cij и поликристаллических (B, G, E) коэффициенты упругости для обоих халькопиритов и фазы каменной соли ZnSiP2.  Для конкретных случаев тетрагональных решеток, модуль массы и сдвига задаются следующими выражениями:  Вычисленные изотропные упругие параметры, а именно BH, GH, E, r для ZnSiP2 халькопирита суммированы в таблице 1. Как Таблица 1 показывает, что значения модуля объемной плотности, полученные с использованием метода усреднения Reuss-Voigt-Hill, хорошо соответствуют значениям, полученным из Birch-Murnaghan EOS соответствует объему сжимаемости. Это служит показателем точности наших прогнозов. Для констант упругости халькопирит ZnSiP2 более резистивен до объемного сжатия, чем до сдвига (B > G). Модуль Е, определенное как отношение напряжения растяжения к соответствующей деформации растяжения, оценивается в 136,4 ГПа, что является показателем повышенной жесткости структуры халькопирита для ZnSiP2. Расчетное значение коэффициента Пуассона равно 0,23 и оно меньше 0,25, где это нижний предел для твердых веществ центральной силы [54], предполагаем, что на исследуемое соединение влияет определенное количество взносов нецентральных сил, что свидетельствует о наличии ковалентного характера в связывании этого материала. Pug [55] предложил простую взаимосвязь, которая эмпирически связывает пластические свойства материалов с их эластичностью. Высокое отношение B/G связано с пластичностью, тогда как Низкое значение соответствует более хрупкой природе, критическое значение которой разделяет пластичные и хрупкие материалы, составляет около 1,75 (соответствует r = 0,26); Т.е. если B/G > 1,75, материал ведет себя пластично; В противном случае материал ведет себя хрупко. Значение отношения B/G для ZnSnP2 халькопирита равно 1,59, таким образом его можно классифицировать как хрупкий материал. (см. Рис. 4).  Рис. 4. Вычисленная зависимость модуля объемного давления (В), модуля Юнга (Е) и модуля сдвига (G) для ZnSiP2 в структурах халькопирита и рокксальта. Сплошные линии являются линейными посадками точек данных (для случая E (P) и G (P) фазы халькопирита сплошные линии являются полиномиальными посадками точек данных наименьшего квадрата второго порядка) Для фазы каменной соли B, G и E увеличиваются линейно относительно изменения давления. В рассматриваемом диапазоне давления для роксальтовой фазы (40-65 ГПа) В, G и Е повышается примерно на 68%, 73% и 36% соответственно. То же самое замечание касается модуля объемной плотности фазы халькопирита; В увеличивается на 138% в диапазоне давлений от 0 до 30 ГПа. Модуль сдвига и модуля Юнга халькопиритной фазы отличается от модуля объемного модуля. Установлено, что G и E немного увеличиваются относительно изменения давления ниже 20 ГПа и затем они начинают снижаться при давлении выше 20 ГПа. Такое поведение можно объяснить снижением механической стабильности халькопиритной фазы с увеличением давления. Кроме того, изменения отношения В/G и отношения Пуассона r относительно давления в двух исследуемых фазах ZnSiP2 показаны на рисунке 5. Можно заметить, что отношение Пуассона и B/G увеличивается в фазе халькопирита и уменьшается в фазе рокксальта.  Рис. 5. Вычисленная зависимость давления от отношения B/G и отношения Пуассона (r) для ZnSiP2 в халькопиритовых и роксальтовых структурах. Например, увеличение r по отношению к повышению давления указывает на тенденцию к механической нестабильности с увеличением давления. Кроме того, из рисунка 5 можно сделать вывод, что приложение давления может улучшить хрупкость или пластичность. |
