Дроби. Как устроена обыкновенная дробь Обыкновенная дробь
 Скачать 264.5 Kb. Скачать 264.5 Kb.
|
|
Как устроена обыкновенная дробь Обыкновенная дробь — это запись вида a/b, где a и b любые натуральные числа. Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая. Числитель обыкновенной дроби a/b — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим. Знаменатель обыкновенной дроби a/b — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим. Черта между числителем и знаменателем — символ деления.  Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2. Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным. Действия с дробями С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем. Сравнение дробей Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше. Сравним 1/5 и 4/5. Как рассуждаем: 1. В обеих дробях знаменатель равен 5. 2. В первой дроби числитель равен 1, во второй дроби равен 4. 1 < 4 3. Поэтому первая дробь 1/5 меньше второй 4/5.  Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше. Сравним 1/2 и 1/8. Как рассуждаем: Представим, что у нас есть торт. Так как знаменатель первой дроби равен 2, то делим торт на две части и забираем себе одну, то есть половину торта. Знаменатель второй дроби равен 8, делим торт на восемь частей и забираем крохотный кусочек. Половина торта больше маленького кусочка. Таким образом 1/2 > 1/8.  Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями. Пример. Сравнить 2/7 и 1/14. Как рассуждаем: 1. Приведем дроби к общему знаменателю: 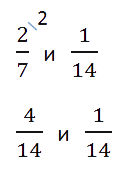 2. Сравним дроби с одинаковыми знаменателями: 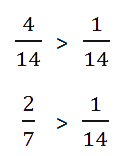 Ответ: 2/7 > 1/14. Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.  Чтобы сравнить дроби с разными числителями и знаменателями, нужно: – привести дроби к общему знаменателю; – сравнить полученные дроби. Чтобы привести дроби к общему знаменателю, нужно: 1. Найти общее кратное знаменателей дробей, которое станет их общим знаменателем. 2. Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель. 3. Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель. Сокращение дробей Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81. Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число. В этом примере делим обе части дроби на двойку.  Можно никуда не спешить и сокращать дроби последовательно, в несколько действий. 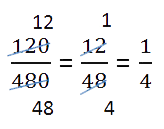 Сложение и вычитание дробей При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель. Не забудьте проверить, можно ли сократить дробь и выделить целую часть.  При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило). Вот, что делать: 1. Найдем наименьшее общее кратное для определения единого делителя.  Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК. 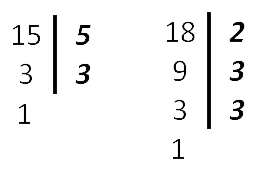 НОК (15, 18) = 3 * 2 * 3 * 5 = 90 2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель: 90 : 15 = 6, 90 : 18 = 5. Полученные числа запишем справа сверху над числителем.  3. Воспользуемся одним из основных свойств дробей: перемножим числитель и знаменатель на дополнительный множитель. После умножения знаменатель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.  4. Проверим полученный результат: – если числитель больше знаменателя, нужно преобразовать дробь в смешанное число; – если есть что сократить, нужно выполнить сокращение. 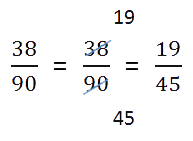 Ход решения одной строкой: 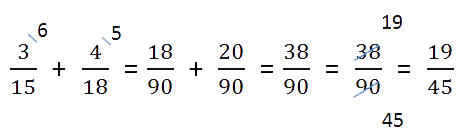 Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно: 1. Сложить целые части. 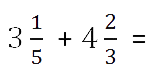 2. Сложить дробные части.  Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера. 3. Суммировать полученные результаты. 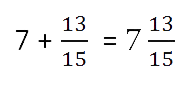 Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части. Умножение и деление дробей Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:  Не забываем про сокращение. Это может облегчить вычисления.  Чтобы умножить два смешанных числа, надо: 1. преобразовать смешанные дроби в неправильные; 2. перемножить числители и знаменатели дробей; 3. сократить полученную дробь; 4. если получилась неправильная дробь, преобразовать в смешанную.  Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий: – числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби; – знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби. Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй. 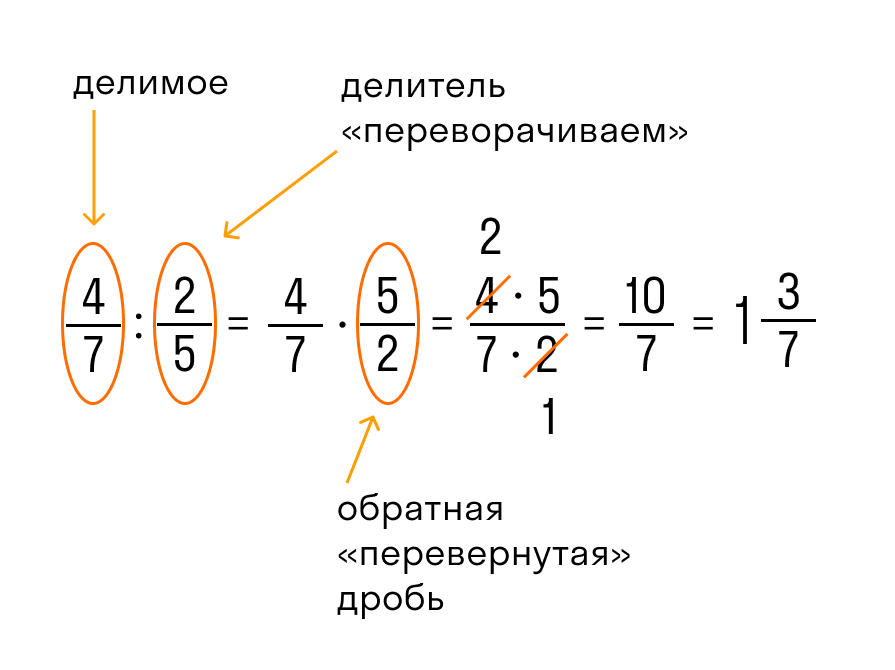 Числа, произведение которых равно 1, называют взаимно обратными. Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше. Для деления смешанных чисел необходимо: – представить числа в виде неправильных дробей; – разделить то, что получилось друг на друга.  |
