математика. ЗО Математика (2 курс) база. Какое понятие не связано с суммой ряда
 Скачать 402.71 Kb. Скачать 402.71 Kb.
|
1 2 *расходится может сходиться, а может расходиться условно сходится Если 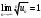 , то знакоположительный ряд , то знакоположительный ряд 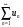 : :сходится расходится *может сходиться, а может расходиться условно сходится Дифференциальные уравнения бывают: обыкновенные и необыкновенные *обыкновенные и в частных производных необыкновенные и в частных производных Дифференциальное уравнение 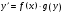 – это: – это:*уравнение с разделяющимися переменными уравнение линейное, однородное однородное уравнение уравнение Бернулли уравнение линейное, неоднородное Дифференциальное уравнение 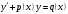 – это: – это:уравнение с разделяющимися переменными однородное уравнение уравнение Бернулли линейное однородное уравнение 1-го порядка *линейное неоднородное уравнение 1-го порядка Дифференциальное уравнение 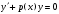 – это: – это:уравнение с разделяющимися переменными однородное уравнение уравнение Бернулли *линейное однородное уравнение 1-го порядка линейное неоднородное уравнение 1-го порядка Решить дифференциальное уравнение – значит: найти значение функции, обращающее уравнение в тождество найти значение логарифма функции, обращающее уравнение в тождество найти значение тангенса функции, обращающее уравнение в тождество найти значение аргумента, обращающее уравнение в тождество *найти функцию, обращающую уравнение в тождество Общее решение неоднородного линейного дифференциального уравнения равно: общему решению однородного линейного ДУ общему решению однородного линейного ДУ плюс произвольная функция частному решению линейного неоднородного ДУ плюс произвольная функция частному решению линейного неоднородного ДУ *сумме частного решения линейного неоднородного ДУ и общего решения линейного однородного ДУ Дифференциальное уравнение 1-го порядка с разделяющимися переменными: 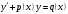 * 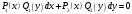 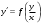 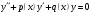 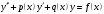 Линейное однородное дифференциальное уравнение 1-го порядка: * 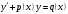 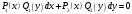 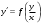 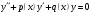 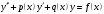 Линейное однородное дифференциальное уравнение 2-го порядка: 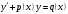 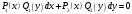 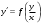 * 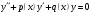 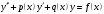 Линейное неоднородное дифференциальное уравнение 2-го порядка: 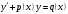 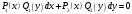 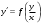 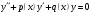 * 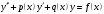 Однородное дифференциальное уравнение 1-го порядка: 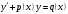 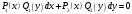 * 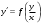 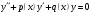 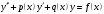 Общее решение дифференциального уравнения 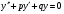 , когда корни характеристического уравнения – действительные и различные числа , когда корни характеристического уравнения – действительные и различные числа 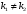 : :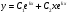 * 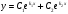 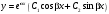 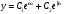 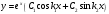 Общее решение дифференциального уравнения 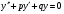 , когда корни характеристического уравнения – действительные равные числа , когда корни характеристического уравнения – действительные равные числа 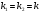 : :* 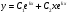 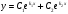 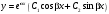 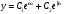 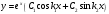 Общее решение дифференциального уравнения 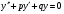 , когда корни характеристического уравнения – комплексные числа , когда корни характеристического уравнения – комплексные числа 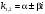 : :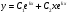 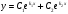 * 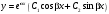 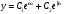 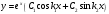 Дифференциальным уравнением называется уравнение, в которое неизвестная функция входит: под знаком интеграла *под знаком производной или дифференциала под знаком логарифма в неявном виде Общим интегралом дифференциального уравнения 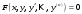 является семейство функций вида: является семейство функций вида:* 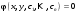 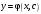 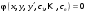 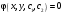 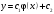 Дифференциальное уравнение 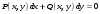 является уравнением в полных дифференциалах, если выполняется условие: является уравнением в полных дифференциалах, если выполняется условие: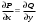 * 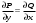 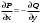 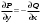 нет верного ответа Два события называются несовместными, если ... *наступление одного из них исключает наступление другого наступление одного из них не исключает наступление другого они происходят одновременно Из 500 деталей на складе 10 оказались бракованными. Какова вероятность взять исправную деталь? 0,02 0,78 *0,98 0,01 0,99 Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер? 0,68 *0,18 0,5 0,33 0,2 На экзамене 25 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный билет. *0,88 1,14 0,12 0,5 0,2 Из 800 автомобилей 8 ломаются в течение 1 года эксплуатации. Какова вероятность купить автомобиль, который не поломается в течение 1 года эксплуатации? 0,01 *0,99 0,8 0,08 0,5 Событие «После зимы наступает лето» является... *невозможным достоверным случайным дискретным непрерывным Из колоды (36 карт) наудачу выбирают одну карту. Какова вероятность, что она окажется пиковой масти? *0,25 0,75 0,5 1/36 0,2 Суммой двух событий называется: новое событие, состоящее в том, что происходят оба события одновременно *новое событие, состоящее в том, что происходит или первое, или второе, или оба вместе новое событие, состоящее в том, что происходит одно, но не происходит другое новое событие, состоящее в том, что происходит или первое, или второе Произведением двух событий называется: *новое событие, состоящее в том, что происходят оба события одновременно новое событие, состоящее в том, что происходит или первое, или второе, или оба вместе новое событие, состоящее в том, что происходит одно, но не происходит другое новое событие, состоящее в том, что происходит или первое, или второе Вероятностью события называется: произведение числа исходов, благоприятствующих появлению события, на общее число исходов сумма числа исходов, благоприятствующих появлению события, и общего числа исходов *отношение числа исходов, благоприятствующих появлению события, к общему числу исходов разность числа исходов, благоприятствующих появлению события, и общего числа исходов Вероятность невозможного события: больше нуля и меньше единицы *равна нулю равна единице больше единицы меньше нуля Вероятность достоверного события: больше нуля и меньше единицы равна нулю *равна единице больше единицы меньше нуля Вероятность случайного события: *больше нуля и меньше единицы равна нулю равна единице больше единицы меньше нуля Указать правильное утверждение: вероятность суммы событий равна сумме вероятностей этих событий вероятность суммы независимых событий равна сумме вероятностей этих событий *вероятность суммы несовместных событий равна сумме вероятностей этих событий Указать правильное утверждение: вероятность произведения событий равна произведению вероятностей этих событий *вероятность произведения независимых событий равна произведению вероятностей этих событий вероятность произведения несовместных событий равна произведению вероятностей этих событий Какие события называются гипотезами? любые попарно несовместные события *попарно несовместные события, объединение которых образует достоверное событие пространство элементарных событий любые события Формулы Байеса определяют: априорную вероятность гипотезы апостериорную вероятность гипотезы *вероятность гипотезы вероятность события Функция распределения случайной величины Х является: невозрастающей *неубывающей произвольного вида монотонной Дискретную случайную величину задают: указывая её вероятности *указывая ее закон распределения поставив каждому элементарному исходу в соответствие действительное число указывая её значения Формула для вычисления среднего квадратического отклонения случайной величины: * 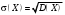 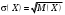 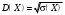 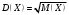 Дисперсия случайной величины вычисляется по формуле: 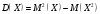 * 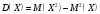 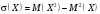 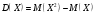 Математическое ожидание дискретной случайной величины вычисляется по формуле: * 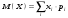 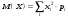 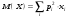 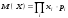 Событий какого вида из перечисленных не существует с точки зрения теории вероятностей? достоверные события невозможные события *решающие события случайные события События называют несовместными, если: установлено, что ни одно из них не может наступить вероятности наступления каждого из событий невозможно определить *в результате одного испытания может наступить одно из этих событий события относятся к разным видам человеческой деятельности В задаче « Производится два выстрела по мишени. Найти вероятность того, что мишень будет поражена один раз» испытанием является: *производится два выстрела по мишени мишень будет поражена один раз мишень будет поражена два раза Бросают монету. Событие  – «выпадет герб». Тогда событие – «выпадет герб». Тогда событие 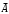 – «выпадет цифра» является: – «выпадет цифра» является:случайным достоверным невозможным *противоположным Подбрасывается игральный кубик. Обозначим события: А – «выпадение 6 очков», В – «выпадение 4 очков», D – «выпадение 2 очков», С – «выпадение четного числа очков». Тогда событие С равно: 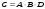 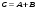 * 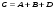 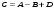 Студент должен сдать два экзамена. Событие А – « студент сдал первый экзамен», событие В – «студент сдал второй экзамен», событие С – «студент сдал оба экзамена». Тогда событие С равно * 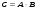 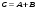 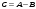 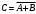 Из букв слова «ЗАДАЧА» наугад выбирается одна буква. Событие – «выбрана буква К» является: случайным достоверным *невозможным противоположным Из букв слова «МИР» наугад выбирается одна буква. Событие – «выбрана буква М» является: *случайным достоверным невозможным противоположным Событие – «из урны, содержащей только белые шары, извлекают белый шар» является: случайным *достоверным невозможным противоположным Два студента сдают экзамен. События: А – «экзамен сдаст первый студент», В – «экзамен сдаст второй студент» являются: несовместными достоверными невозможными *совместными События называют несовместными, если: наступление одного не исключает возможность появления другого при осуществлении комплекса условий каждое из них имеет равную возможность наступить при испытании обязательно наступит хотя бы одно из них *наступление одного исключает возможность появления другого В урне 12 шаров, ничем, кроме цвета, не отличающихся. Среди этих шаров 5 черных и 7 белых. Событие – «случайным образом извлекают белый шар». Для этого события число благоприятствующих исходов равно: 12 5 *7 1 В урне 12 шаров, ничем, кроме цвета, не отличающихся. Среди этих шаров 5 черных и 7 белых. Событие – «случайным образом извлекают белый шар». Для этого события число всех исходов равно: *12 5 7 1 Вероятность события принимает любое значение из промежутка: 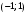 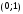 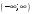 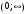 * 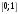 Дана задача: «В круг вписан треугольник. В круг наудачу брошена точка. Какова вероятность того, что эта точка попадет в треугольник?» Для решения этой задачи необходимо использовать: классическое определение вероятности *геометрическое определение вероятности формулу Бернулли формулу Байеса Заготовка может поступить для обработки на один из двух станков с вероятностями 0,7 и 0,3 соответственно. Вероятность брака для первого станка равна 0,2, для второго равна 0,1. Найти вероятность того, что наугад взятая деталь бракованная. Задача решается с использованием: теоремы сложения вероятностей совместных событий теоремы умножения вероятностей зависимых событий *формулы полной вероятности формулы Байеса классического определения вероятности Задача «В магазин вошло 5 покупателей. Найти вероятность того, что 4 из них совершат покупки, если вероятность совершить покупку для каждого из них равна 0,7» решается с использованием: теоремы сложения вероятностей совместных событий *формулы Бернулли формулы полной вероятности формулы Байеса классического определения вероятности Задача «В магазин вошло 500 покупателей. Найти вероятность того, что 44 из них совершат покупки, если вероятность совершить покупку для каждого из них равна 0,7» решается с использованием *локальной теоремы Лапласа формулы Бернулли формулы полной вероятности формулы Байеса классического определения вероятности Для нахождения вероятности того, что при 200 бросаниях игральной кости три очка появятся от 100 до 150 раз, используется локальная теорема Лапласа *интегральная теорема Лапласа формула полной вероятности формула Байеса классическое определение вероятности Случайная величина X называется распределенной по биномиальному закону, если … * 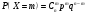 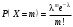 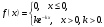 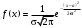 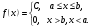 Случайная величина X называется распределенной по закону Пуассона, если … 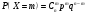 * 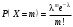 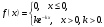 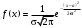 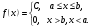 Случайная величина X называется равномерно распределенной на интервале 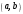 , если … , если …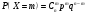 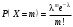 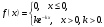 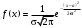 * 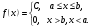 Математическое ожидание и дисперсия непрерывной случайной величины X, распределенной по показательному закону 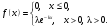 равны:  , ,  * 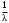 , , 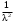  , , 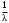 1, 0 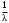 , ,  Случайная величина X имеет показательное распределение, если … 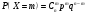 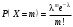 * 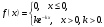 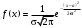 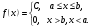 Случайная величина X имеет нормальное распределение, если … 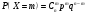 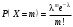 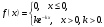 * 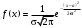 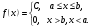 Математическое ожидание и дисперсия непрерывной биномиально распределенной случайной величины X, равны …  , , 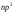 * 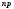 , , 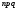 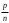 , ,   , , 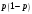  , , 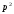 Чем отличаются друг от друга различные перестановки из n элементов? количеством элементов нет ни одного верного варианта ответа количеством и составом элементов ничем не отличаются составом элементов *только порядком расположения элементов Какое событие называется противоположным событию А? событие, всегда наступающее в результате опыта событие, никогда не наступающее в результате опыта нет ни одного верного варианта ответа *событие, состоящее в ненаступлении события А Какое событие называется произведением AB событий А и В? событие, состоящее в наступлении хотя бы одного из событий А или В *событие, состоящее в их совместном наступлении нет ни одного верного варианта ответа событие А происходит, а В − не происходит событие, состоящее в наступлении только одного из событий A или В Чем отличаются друг от друга различные размещения из n элементов по m? количеством элементов ничем не отличаются нет ни одного верного варианта ответа *порядком расположения элементов либо их составом только составом элементов Чем отличаются друг от друга различные сочетания из n элементов по m? порядком расположения элементов либо их составом количеством и составом элементов ничем не отличаются только порядком расположения элементов нет ни одного верного варианта ответа *только составом элементов Чему равна вероятность суммы двух произвольных событий? произведению вероятностей этих событий *сумме вероятностей этих событий минус вероятность их произведения сумме вероятности одного из событий и условной вероятности другого, вычисленной при условии, что первое событие наступило сумме вероятностей этих событий нет ни одного верного варианта ответа Чему равна вероятность произведения двух произвольных событий? нет ни одного верного варианта ответа сумме вероятностей этих событий минус вероятность их произведения произведению вероятностей этих событий сумме вероятностей этих событий *произведению вероятности одного из событий на условную вероятность второго, вычисленную при условии, что первое событие наступило Какое событие называется суммой A+B событий А и В? событие, состоящее в их совместном наступлении событие, состоящее в наступлении только одного из событий А или В нет ни одного верного варианта ответа *событие, состоящее в наступлении хотя бы одного из событий А или В Какое из следующих утверждений относительно дискретной случайной величины верно? её значения непрерывно меняются на некотором промежутке нет ни одного верного варианта ответа её значения обязательно целые *множество её значений дискретное или счётное для дискретных случайных величин существует плотность вероятности она не может принимать отрицательные значения Какое из следующих утверждений относительно непрерывной случайной величины верно? её значения изолированы друг от друга множество её значений дискретное или счётное её значения всегда положительны *её значения непрерывно меняются на некотором промежутке для неё существует ряд распределения нет ни одного верного варианта ответа В каких случаях применима формула Пуассона? всегда применима при большом числе опытов применима всегда нет ни одного верного варианта ответа *если число опытов  велико ( велико (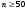 ) вероятность ) вероятность  события А мала и произведение события А мала и произведение 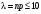 Может ли в схеме испытаний Бернулли меняться от опыта к опыту вероятность наступления события А? может *должна оставаться постоянной всегда меняется нет ни одного верного варианта ответа Для каких случайных величин существует функция распределения? только для величин, принимающих целые значения только для непрерывных только для величин, принимающих положительные значения *для любых только для дискретных Может ли в схеме испытаний Бернулли факт наступления события А в одном из опытов влиять на возможность его появления в остальных опытах? *не может влиять всегда влияет влияет только при большом числе опытов нет ни одного верного варианта ответа не влияет только при малой вероятности события А Возможно ли совместное наступление двух или более из гипотез 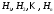 при использовании формулы полной вероятности или формулы Байеса? при использовании формулы полной вероятности или формулы Байеса?*нет, гипотезы должны взаимно исключать друг друга конечно, возможно, только так и бывает возможно, если событие А не зависит от гипотез нет ни одного верного варианта ответа возможно, если событие А зависит от гипотез Какое утверждение относительно гипотез 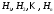 в формуле полной вероятности и в формуле Байеса не является верным? в формуле полной вероятности и в формуле Байеса не является верным?*событие А не зависит от гипотез событие А обязательно наступает в совокупности с одной из гипотез, т.е. зависит от них сумма вероятностей гипотез всегда равна единице гипотезы обязательно образуют полную группу попарно несовместных событий Какое из следующих утверждений относительно функции распределения случайной величины не является верным? при бесконечном увеличении аргумента функция стремится к единице это неубывающая функция *при бесконечном уменьшении аргумента функция стремится к единице она всегда заключена между нулём и единицей Теория вероятностей – это… изучение вероятностей *раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними центральное понятие теории вероятностей раздел математики случайные события события Число размещений без повторений определяется формулой: 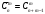 * 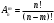 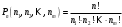 , где , где 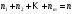 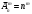 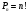 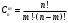 Число размещений с повторениями определяется формулой: 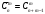 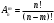 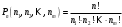 , где , где 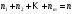 * 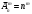 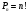 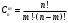 Число перестановок без повторений определяется формулой: 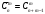 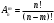 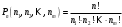 , где , где 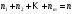 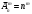 * 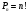 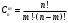 Число перестановок с повторениями определяется формулой: 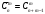 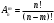 * 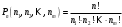 , где , где 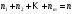 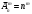 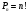 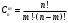 Число сочетаний без повторений определяется формулой: 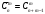 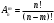 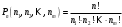 , где , где 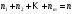 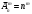 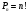 * 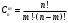 Число сочетаний с повторениями определяется формулой: * 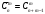 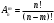 1 2 |
