математика. ЗО Математика (2 курс) база. Какое понятие не связано с суммой ряда
 Скачать 402.71 Kb. Скачать 402.71 Kb.
|
1 2 Какое понятие не связано с суммой ряда? частичная сумма приближенные суммы *дискретная сумма сумма n первых членов К применению признака сравнения не относится: есть ряд, сходимость которого известна есть ряд, расходимость которого известна используется геометрический ряд *вычисляются интегралы общих членов рядов Если радиус сходимости для степенного ряда 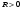 , то этот ряд сходится на интервале: , то этот ряд сходится на интервале: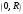 * 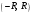 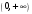 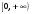 Если при исследовании ряда на сходимость по признаку Даламбера установлено, что 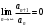 , это означает, что: , это означает, что:*ряд сходится ряд расходится ряд может, как сходиться, так и расходиться вопрос о сходимости остаётся открытым Если при исследовании ряда на сходимость по признаку Даламбера установлено, что 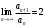 , это означает, что: , это означает, что:ряд сходится *ряд расходится ряд может, как сходиться, так и расходиться вопрос о сходимости остаётся открытым Ряд 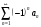 , , 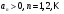 , называется… , называется…*знакочередующимся степенным знакопеременным знакоположительным Ряд 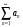 называется… называется…знакочередующимся степенным *знакопеременным знакоположительным Ряд 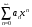 называется… называется…знакочередующимся *степенным знакопеременным знакоположительным Ряд 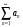 , , 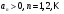 , называется… , называется…знакочередующимся степенным знакопеременным *знакоположительным Ряд 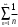 называется… называется…рядом геометрической прогрессии степенным *гармоническим обобщенным гармоническим Ряд 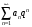 называется… называется…*рядом геометрической прогрессии степенным гармоническим обобщенным гармоническим Ряд 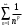 , , 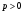 , называется… , называется…рядом геометрической прогрессии степенным гармоническим *обобщенным гармоническим Дан ряд 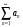 , , 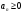 . Рассмотрим . Рассмотрим 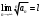 . Тогда: . Тогда:если 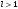 , то ряд сходится , то ряд сходитсяесли 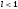 , то ряд расходится , то ряд расходится*если 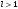 , то ряд расходится , то ряд расходитсяесли 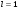 , то ряд сходится , то ряд сходитсяДан ряд 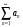 , , 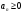 . Рассмотрим . Рассмотрим 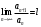 . Тогда: . Тогда:*если 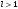 , то ряд расходится , то ряд расходитсяесли 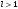 , то ряд сходится , то ряд сходитсяесли 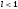 , то ряд расходится , то ряд расходитсяесли 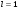 , то ряд сходится , то ряд сходитсяДан ряд 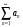 , , 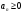 . Рассмотрим . Рассмотрим 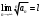 . Тогда: . Тогда:если 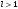 , то ряд сходится , то ряд сходитсяесли 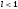 , то ряд расходится , то ряд расходится*если 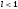 , то ряд сходится , то ряд сходитсяесли 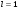 , то ряд сходится , то ряд сходитсяДан ряд 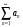 , , 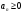 . Рассмотрим . Рассмотрим 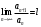 . Тогда: . Тогда:*если 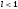 , то ряд сходится , то ряд сходитсяесли 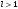 , то ряд сходится , то ряд сходитсяесли 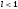 , то ряд расходится , то ряд расходитсяесли 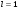 , то ряд сходится , то ряд сходитсяЕсли ряд из абсолютных величин знакочередующегося ряда сходится, то знакочередующийся ряд: сходится условно может как сходиться условно, так и расходиться *сходится абсолютно расходится Необходимый признак сходимости числового ряда: если ряд 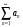 сходится, то… сходится, то…* 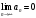 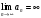 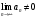 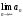 не существует не существуетДостаточный признак сходимости числового ряда: ряд 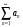 расходится, если… расходится, если…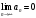 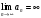 * 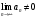 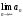 не существует не существуетПризнак сравнения рядов 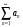 (1) и (1) и 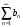 (2) с положительными членами при (2) с положительными членами при 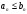 для всех для всех 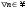 : :если ряд (1) сходится, то ряд (2) расходится если ряд (1) сходится, то и ряд (2) сходится *если ряд (2) сходится, то и ряд (1) сходится если ряд (2) расходится, то и ряд (1) расходится Признак сравнения рядов 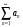 (1) и (1) и 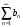 (2) с положительными членами при (2) с положительными членами при 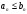 для всех для всех 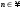 : :если ряд (1) сходится, то ряд (2) расходится если ряд (1) сходится, то и ряд (2) сходится если ряд (2) расходится, то и ряд (1) расходится *если ряд (1) расходится, то и ряд (2) расходится Признак Лейбница для ряда 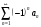 : :*если 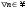 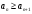 и и 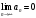 , то ряд сходится , то ряд сходитсяесли 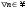 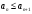 и и 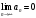 , то ряд сходится , то ряд сходитсяесли 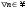 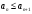 и и 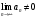 , то ряд сходится , то ряд сходитсяесли 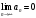 , то ряд сходится , то ряд сходитсяДан знакочередующийся ряд 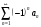 (1) и ряд, составленный из модулей его членов (1) и ряд, составленный из модулей его членов 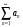 (2). Тогда: (2). Тогда:*если ряд (2) сходится, то ряд (1) сходится абсолютно если ряд (2) расходится, то ряд (1) расходится если ряд (2) сходится, то ряд (1) сходится условно если ряд (2) расходится, то ряд (1) расходится условно Дан знакочередующийся ряд 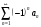 (1) и ряд, составленный из модулей его членов (1) и ряд, составленный из модулей его членов 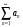 (2). Тогда: (2). Тогда:если ряд (2) сходится, то ряд (1) сходится *если ряд (2) расходится, а ряд (1) сходится, то ряд (1) сходится условно если ряд (2) сходится, то ряд (1) сходится условно если ряд (2) расходится, то ряд (1) расходится условно Радиус сходимости степенного ряда 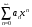 находят по формуле: находят по формуле: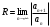 * 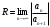 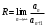 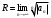 Радиус сходимости степенного ряда 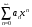 находят по формуле: находят по формуле: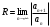 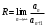 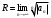 * 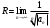 Разложение функции 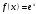 в ряд Маклорена имеет вид: в ряд Маклорена имеет вид: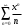 * 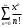 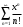 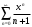 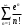 Разложение функции 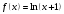 в ряд Маклорена имеет вид: в ряд Маклорена имеет вид: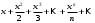 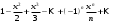 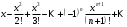 * 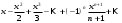 Разложение функции 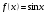 в ряд Маклорена имеет вид: в ряд Маклорена имеет вид:* 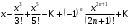 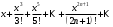 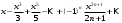 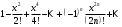 Разложение функции 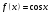 в ряд Маклорена имеет вид: в ряд Маклорена имеет вид: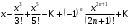 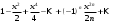 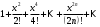 * 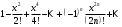 Разложение функции 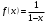 в ряд Маклорена имеет вид: в ряд Маклорена имеет вид:* 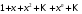 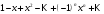 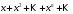 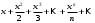 Разложение функции 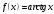 в ряд Маклорена имеет вид: в ряд Маклорена имеет вид: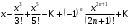 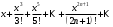 * 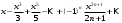 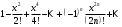 Разложение функции 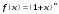 в ряд Маклорена имеет вид: в ряд Маклорена имеет вид: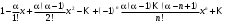 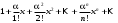 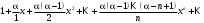 * 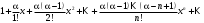 Известно, что ряд 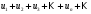 сходится. Тогда ряд сходится. Тогда ряд 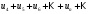 : :*сходится расходится может сходиться, а может расходиться условно сходится Если 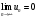 , то ряд , то ряд 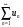 : :сходится расходится *может сходиться, а может расходиться условно сходится Если 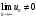 , то ряд , то ряд 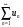 : :сходится *расходится может сходиться, а может расходиться условно сходится Если 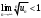 , то знакоположительный ряд , то знакоположительный ряд 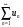 : :*сходится расходится может сходиться, а может расходиться условно сходится Если 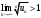 , то знакоположительный ряд , то знакоположительный ряд 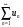 : :сходится 1 2 |
